信息论基础概念、定理(一)
熵、相对熵、互信息
熵、信息量
信息量\(I = -\log(P)\)
- 对称
- 非负
条件熵、联合熵
联合熵链式法则
\[H(X,Y) = H(X|Y) + H(Y)$$(联合熵增) $$H(X,Y|Z) = H(X|Z) + H(Y|X,Z)$$?? \]
相对熵、互信息
- \(D \geq 0\)
- Jensen不等式
- log 严格凸函数
- 非对称
- 相对熵不是距离
- 互信息与相对熵
- \(I(X;Y) = D(p(x,y)||p(x)p(y)) \geq 0\)
- \(I(X;Y) = \min D(p_{XY}||q_{X}q_{Y})\)
- 互信息就是最相似的独立分布的相对熵
- \(D(p_{XY}||q_{X}q_{Y}) - D(p_{XY}||p_{X}p_{Y})\)
\[I(X;Y) = H(X)-H(X|Y) = H(Y)-H(Y|X) \]
熵的链式法则
\[H(X_{1},\dots,X_{n}) =H(X_{1})+H(X_{2}|X_{1}) + H(X_{3}|(X_{1},X_{2})) \]
条件互信息
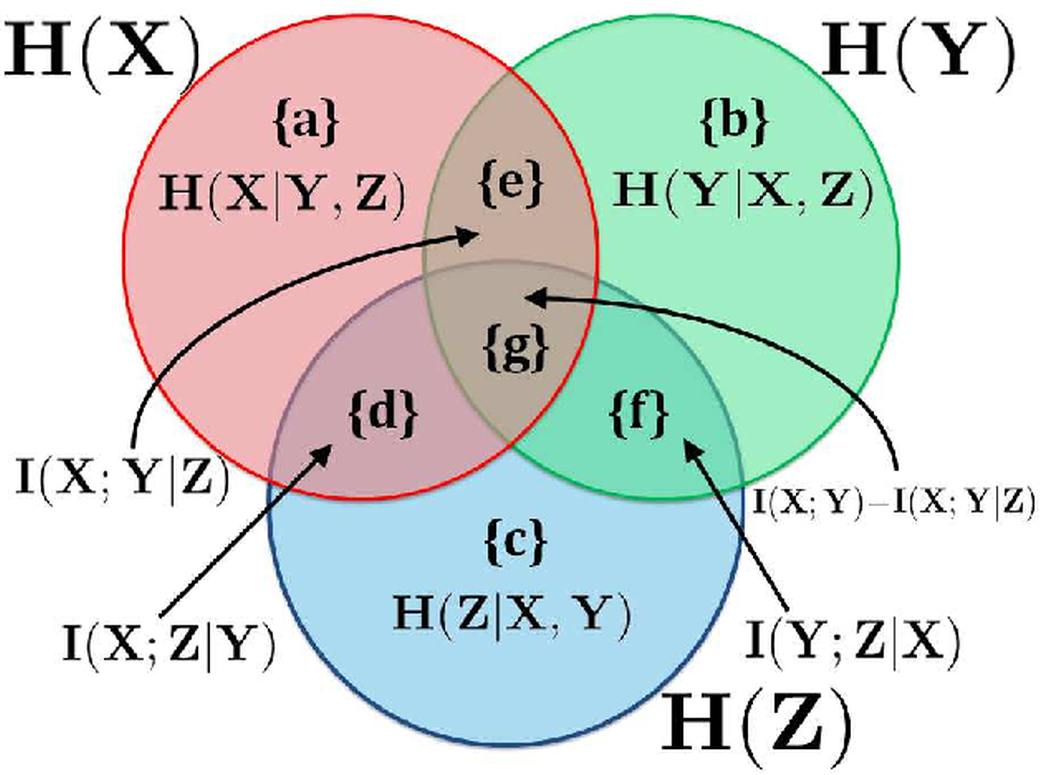
given 哪个变量,就相当于在韦恩图当中抠除哪个变量
互信息的链式法则
\[I((X_{1},\cdots,X_{n});Y) = I(X_{1};Y) + I(X_{2};Y|X_{1}) \]
条件相对熵
相对熵的链式法则
联合=自身+条件\[D(p(x,y)||q(x,y)) = D(p(x)||q(x)) + D(p(y|x) + D(x|y)) \]
条件熵的性质
\[D(p||q) \leq 0 \]
Jensen不等式
Jensen不等式:对于凸函数\(f\)以及随机变量\(X\)
\[Ef(X) \geq f(EX) \]
几个定理
条件互信息的非负性
\[I(X;Y|Z) = D(p(x,y|z)||p(x|z),p(y|z)) \geq 0 \]当且仅当x,y关于z条件独立,等号成立
\[H(X)\leq \log|\mathcal{X}| \]
\[H(X) - H(X|Y) = I(X;Y) \geq 0 \]
熵的独立界
\[\begin{align*} H(X_{1},\cdots,X_{n}) &= H(X_{1}) + H(X_{2}|X_{1}) + H(X_{3}|X_{1},X_{2}) \\ &\leq \sum H(X_{i}) \end{align*}\]当且仅当\(X_{i}\)相互独立时等号成立
马尔可夫分布
如果不记得符号可以自己定义
数据处理不等式
\(X\to Y\to Z\)
- \(I(X;Z) \leq I(X;Y)\)
- 互信息不增加
- $I(X;Y|Z) = 0 \leq $
Fano 不等式
费诺不等式
\[X\to Y \to \hat{X} \]\[H(P_{e}) + P_{e}\log(|\mathcal{X}|) \geq H(X|\hat{X})\geq H(X|Y) \]\[1+ P_{e}\log(|\mathcal{X}|) \geq H(X|Y) \]\[P_{e}\geq \frac{H(X|Y)-1}{\log|\mathcal{X}|} \]
费诺不等式的几个推论
渐进均分性
信息论重要概念
AEP
AEP的基础:辛钦大数定律(频率依概率收敛)

含义解释
随着序列增长,一个长度为n的序列出现的概率将会趋近一个和熵有关的值:\(2^{-nH}\)。序列越长,这个概率的估计就会越准确
⭐典型集
for iid \(x_{1},\dots,x_{n}\),\(\mathbf{x}^{(n)} = \{x_{i}\}_{i= 1}^{n}\)
典型集由序列长度\(n\)和误差限\(\varepsilon\)确定

典型集的性质
-
元素出现概率
\[-\frac{1}{n}\log p(\mathbf{x}^{(n)}) \in [H-\varepsilon,H+\varepsilon] \] -
典型集元素概率估计的准确性
\[\begin{align*} \text{Pr}\{A_{\varepsilon}^{(n)}\} &= \text{Pr}(|p(\mathbf{x}^{(n)})-2^{-nH(X)}|> \varepsilon) \\&> 1-\varepsilon \\ \mathbf{x}^{(n)}\in A_{\varepsilon}^{(n)} \end{align*} \] -
典型集包含的序列个数
- 总有
\[|A_{\varepsilon}^{(n)}| \leq 2^{n(H(x)+\varepsilon)} \]- 当n充分大时
\[(1-\varepsilon)2^{n(H(x)-\varepsilon)}\leq |A_{\varepsilon}^{(n)}| \]
熵与平均码长
熵与平均码长的关系:对于任意小的\(\varepsilon\),以及iid\(X\sim p(x)\)生成的序列\(\mathbf{x}^{(n)}\),如果n充分大,则存在可逆编码
\[E(\frac{1}{n}l(\mathbf{x^{(n)}})) \leq H + \varepsilon \]
随机过程
定义
stochastic process is simply an indexed sequence of random variables.
- 随机过程
- \(\text{Pr}(X^{n}= x^{n})\)
- 代表分布的演变过程
- \(x^{n}\)是不同状态上的一个概率分布
- 平稳
-
\[p(x_{1},x_{2},\cdots,x_{n}) = p(x_{1+\Delta t},x_{2+\Delta t},\cdots,x_{n+\Delta t}) \]
-
- 马尔可夫
- 条件独立
-
\[p(x_{n+1}|x_{1},\cdots,x_{n})= p(x_{n+1}|x_{n}) \]
- 时间不变马尔可夫
- \(p(x_{n+1}|x_{n}) = p(x_{2}|x_{1})\text{const}\)
- 通常假定马尔可夫过程具有时间不变性
时间不变的马尔可夫过程可以由概率转移矩阵\([P_{ij}]\)表征
- 不可约
- 任意状态间,有限步可达
- 非周期
- 每个状态经过不同路径回到自身,路径长度不可约??
马尔可夫性
基本定义

条件可约
平稳分布
若有限状态马尔可夫链是不可约的和非周期的,则它的平稳分布唯一
\[n\to \infty, X^{n} \to X^{*} \]
如何计算平稳分布
给我一个随机过程
就是一个概率转移矩阵
给定概率转移矩阵,计算平稳分布

熵率
每字符熵、极限条件熵
- Question: 如何定义一个序列的熵?\(H(X_{1},\cdots,X_{n})\)随机过程的熵,就是针对这个\(X_{i}\)序列所生成的联合概率,计算出来的信息熵。
也就是说,序列的熵,就是随机变量序列的联合熵

熵率是用来刻有时序依赖关系的序列的熵增长速度的物理量
定理:对于平稳随机过程
- 极限平均字符熵 = 极限条件熵
平稳随机过程的若干结论
序列条件熵递减
\[\begin{align*} H(X_{n}|X^{n-1}) &\leq H(X_{n}|X_{2},\cdots,X_{n-1}) \tag*{remove $X_{1}$} \\ &\leq H(X_{n-1}|X^{n-2}) \tag*{stationarity} \\ &\leq H(X_{i}|X^{i-1}) \tag*{for every $i<n$} \end{align*}\]
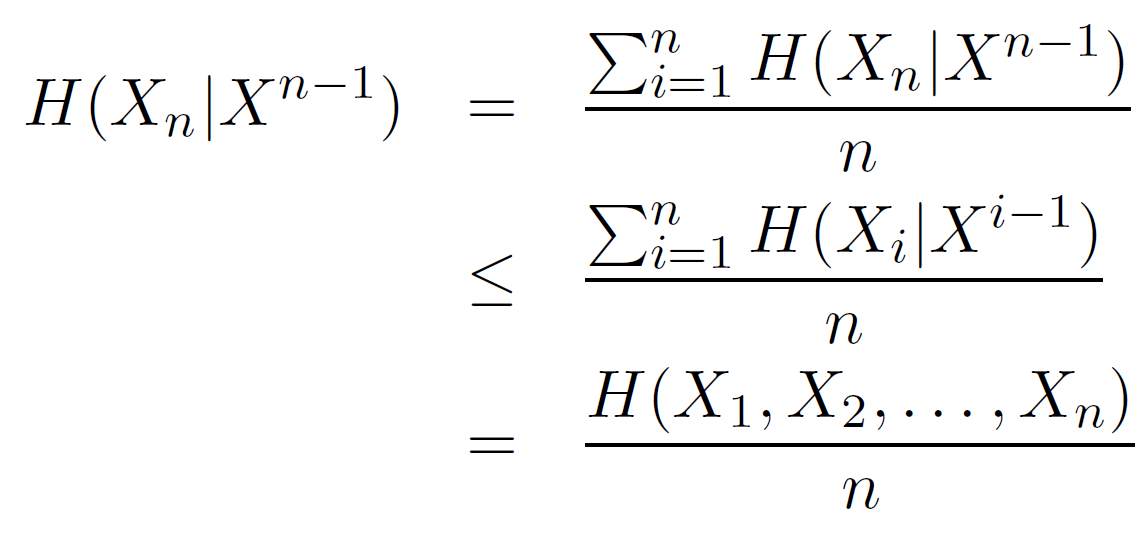
初始条件熵递增
\[\begin{align*} H(X_{n}|X_{1}) &\geq H(X_{n}|X_{2},X_{1})\tag*{add condition} \\&=H(X_{n}|X_{2}) \\&=H(X_{n-1}|X_{1}) \end{align*}\]另有
\[\begin{align*} &H(X_{0}|X_{n}) = H(X_{0}) - I(X_{0};X_{n}) \\&H(X_{0}|X_{n+1}) = H(X_{0}) - I(X_{0};X_{n+1}) \\&H(X_{0}|X_{n+1}) - H(X_{0}|X_{n})=I(X_{0};X_{n}) - I(X_{0},X_{n+1})\geq 0 \tag*{DPI} \end{align*}\]
平稳马尔可夫链的熵率

加权图上随机游动的熵率
例题

热力学第二定律
一些很有趣的结论
数据压缩/最短期望码长
定义
-
信源
- 期望码长
- 非奇异
- 字母不同,编码不同
- 唯一可译码
- 任一编码字符串只来源于惟一可能的倌说字符串
- 前缀码=即时码
- D叉树
非奇异码>唯一可译码>即时码
Kraft不等式
前缀码存在的充要条件
最优前缀码的界
随机变量X的任一D元即时码的期望长度必定大于或等于\(H_{D}(X)\)
- 利用
拉格朗日乘子法证明最优码长的下界 - 利用
相对熵的非负性证明
- 最大信息容量
- 最短码长
随机过程
平稳过程
对于平稳过程
其中
为长度为\(n\)的序列\(\mathbf{x}_{i}^{n}\)的平均码字长度
唯一可译码充要条件/McMillan不等式
从码字长度集的角度考虑,惟一可译码类不能提供比前缀码类更优的选择
香农编码/偏码

十进制小数转二进制
乘二取整

- Question: 编码都只是针对信源吗?
- Question: 信源都是不变的吗?
香农码具有竞争最优性
哈夫曼编码是最优编码
最优码有很多
最优码的性质
- 最长的两个码字
- 具有相同长度
- 仅在最后一位上有所差别,且对应于两个最小可能发生的字符
- 其长度序列与按概率分布列排列的次序相反
对于二进制分布,赫夫曼码与香农码相同,且平均码长都达到熵界
Shannon-Fano-Elias 编码
形式化定义,理论分析更加方便
竞争最优性
香农码具有竞争最优性
均匀比特生成任意分布
一个\(p(Z=0) = 0.5\)的信源就是一个产生均匀比特的信源。
给定一个均匀比特串, 可以将其映射到某个分布上
定理:对于任意一个随机变量\(X\),可以用一个完全二叉树进行编码,生成\(X\)对应分布的编码,设这个编码的期望长度为T
\[ET \in [H(X),H(X)+2) \]
平均抛掷\(H(X)+2\)次硬币就足够摸拟随机变量\(X\)了
- Question: 平均的含义是什么
+ Note: 意思应该是对于X的一个取值x,平均需要ET个均匀比特进行编码
+ 也就是期望的均匀比特数
- Question: 为什么这个结论和哈夫曼码的期望码长不一样呢
- 感觉哈夫曼树就是一个最优的均匀比特编码方案啊
+ Note: 也就是说这种编码方案不是最优码
- Question: 这里有明确的编码方案吗
信道容量
信息论的中心问题
定义
信道
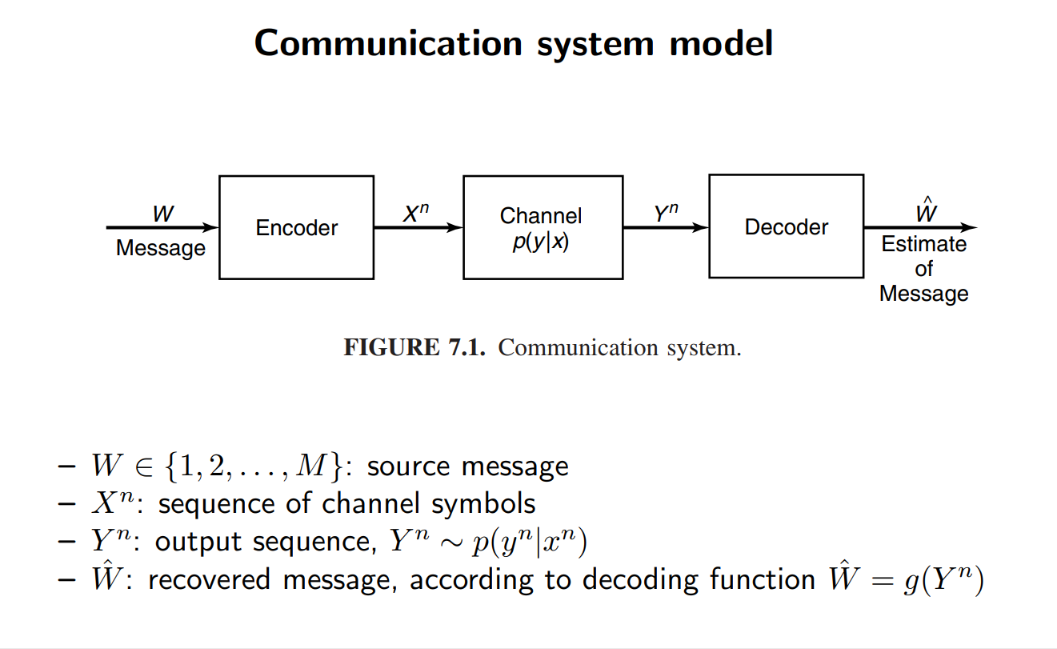
- 离散无记忆信道
- Question: 为什么不用H(X|Y)定义?
- H(X|Y) = H(X) - I(X;Y)

\(p(x)\)指代所有可能都输入分布
- Question: 什么意思?
常见信道容量
-
无噪声二元信道 & 无重叠输出的有噪声信道
- \(1\)
-
有噪声的打字机信道
- P122 无噪声子集?
-
二元对称信道(有噪声)
-
\(1-H(p)\)
证明
\[\begin{align*} C &= \max_{p(X)}I(X;Y) \\&= \max_{p(X)}H(X) - H(X|Y) \end{align*}\]注意:熵只和分布的形态有关,和变量的取值本身没有关系\[\begin{align*} H(X|Y) &= \sum_{y \in \mathcal{Y}}p(y)H(X|Y = y) \\&= \sum_{y \in \mathcal{Y}}p(y)H(p) \\&= H(p) \end{align*}\]\[\begin{align*} C &= \max_{p(X)} H(X) - H(p) \\&= 1 - H(p) \end{align*} \]
-
-
二元可擦除信道
-
\(1-p\)
证明
设\(p(x = 0) = p\)
\[\begin{align*} C &= \max_{p} H(p)- \sum_{y\in \mathcal{Y}}p(y)H(X|Y = y) \\&=\max_{p}H(p)- [p(1-\alpha)\times 0 + (1-p)(1-\alpha)\times 0 + \alpha] \\&= \max_{p}H(p)- \alpha \\&=1-\alpha \end{align*}\]
-
对称信道
定义
- 对称
- 弱对称
对于弱对称信道有
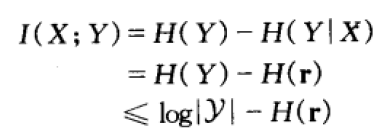
\(C = \log(|\mathcal{Y}|)-H(\text{row})\)
\(\mathcal{Y}\)是矩阵的列数,当输入字母表上的分布为均匀对达到该容量。
信道容量的一些性质
- \(C\geq 0\)
- \(C\leq \log|\mathcal{X}|,C\leq \log|\mathcal{Y}|\)
- \(I(X;Y)\)是关于\(p(x)\)的连续凹函数,只有一个全局最大值
信道编码定理
离散无记忆信道
离散信道的形式化
- 输入集合\(\mathcal{X}\)
- 概率转移矩阵\(p(y|x)\)(以字母为元素)
- 输出字母集\(\mathcal{Y}\)
(M,n)码
- 下标集
- 序列当中每个元素\(\text{seq}_{i} = s_{i}\)的序号\(i \in \{1,\cdots,M\}\)
- 编码函数
- \(f:\{i\} \text{ i.e. } \{s_{i}\} \to \mathbf{x}_{i}^{(n)} \in \mathcal{X}^{n}\)
- 码簿
- \([x^{(n)}(1),\cdots,x^{(n)}(M)]\)
- 译码函数(deterministic function)
- \(g:\mathbf{x}_{i}^{(n)} \to \{i\} \text{ i.e. } s_{i}\)
- 条件误差概率\(\lambda_{i}\)
- 发送信息\(i\)时的出错概率
- 最大误差函数
- 平均误差概率
- \(P_{e}^{(n)} \leq \lambda_{(n)}\)
- 码率:\(R = \log\frac{M}{n}\)
- 表示信道每个字符负责代表多少个原始数据

- 可达,对于\((\lceil2^{nR}\rceil,n)\)码
- \(n\to 0,\lambda^{(n)} \to n\)
- 信道容量 =
可达码率的上确界
联合典型序列
定义

这类似于典型集的定义
即
联合AEP
前提
- \(X^{(n)},Y^{(n)} = \{(x^{(n)},y^{(n)}):p(x^{(n)},y^{(n)}) = \prod p(x_{i},y_{i})\}\)
- 序列生成,各个时间步独立
- 各个序列独立同分布
性质
-
序列有很高概率包含在典型集当中
- Question: 这里的高概率是什么意思 - 一个序列是否在典型集中不是一个确定的事情吗?- \(n\to\infty,\text{Pr}[(x^{(n)},y^{(n)} )\in A_{\varepsilon}^{(n)}]\to 1\)
-
联合典型序列的大小有上界
-
\[|A_{\varepsilon}^{(n)}| \leq 2^{n(H(X,Y) + \varepsilon)} \]
-
-
如果\(\tilde{X}^{(n)},\tilde{Y}^{(n)}\)具有相同边际分布\(p(x^{n}) = p(y^{n})\),那么联合典型序列估计的概率准确性\(\pi= \text{Pr}\{(x^{n},y^{n})\in A_{\varepsilon}^{(n)}\}\)也有上下界
- \(\pi \leq 2^{-n(I(X;Y)-3\varepsilon)}\)
- \(\pi \geq (1-\varepsilon)2^{-n(I(X;Y)+3\varepsilon)}\)
和单一分布AEP相比
- \(|A_{\varepsilon}^{(n)}| \leq 2^{n(H(x) _+\varepsilon)}\)
- \(|A_{\varepsilon}^{(n)}| \geq (1-\varepsilon)2^{n(H(x) - \varepsilon)}\)
联合典型序列的理解

可能的输入序列\(X^{n}\)存在典型集,规模为\(|A(X)| \simeq 2^{n(H(X))}\)
可能的输出序列\(X^{n}\)存在典型集,规模为\(|A(Y)| \simeq 2^{n(H(Y))}\)
给定输入,输出的映射有典型集\(|A(Y|X)| \simeq 2^{H(Y|X)}\)
因此,可区分的输入序列数量为
\(\frac{A(Y)}{A(Y|X)} = 2^{I(X;Y)}\)
任意其他码字与接收到的序列是联合典型的概率是\(2^{I(X;Y)}\)
联合典型序列\(|A(X,Y)| \simeq 2^{H(X,Y)}\)
这个定理有什么实际用途吗
信道编码定理:可达性
对于传输过程(这是一个马尔可夫链)

- \((\lceil 2^{nR}\rceil,n)\)码满足最大误差概率\(\lambda^{(n)}\to 0\)
- \(R<C\)
二者等价
多次使用信道井不增加每次传输的信息容量比特
- \(H(W|\hat{W}) \leq 1 + P_{e}^{(n)}\)
- \(I(Y^{(n)};X^{(n)}) \leq nC\)
信道编码定理的逆定理:平均误差概率
\(W \sim \text{Uni}(\{1,2,\cdots,2^{nR}\})\)
\(H(W) = -n\frac{1}{n}\log \frac{1}{n} = \log n\)

如何达到最大码率

带反馈的信道
(X_{1};X_{4}|X_{2}) \overset{\text{条件独立}}{=}0$$反馈在简化编码和译码方面可以起到很大的作用。然而,它并不能增加信道的容量。
信源信道分离定理
- 每字符最小期望码长,对于随机平稳过程,\(l^{*} \to H(\mathcal{X})\)
- Question: 为什么书里写的是R>H - 信道编码定理,\(R<C\)
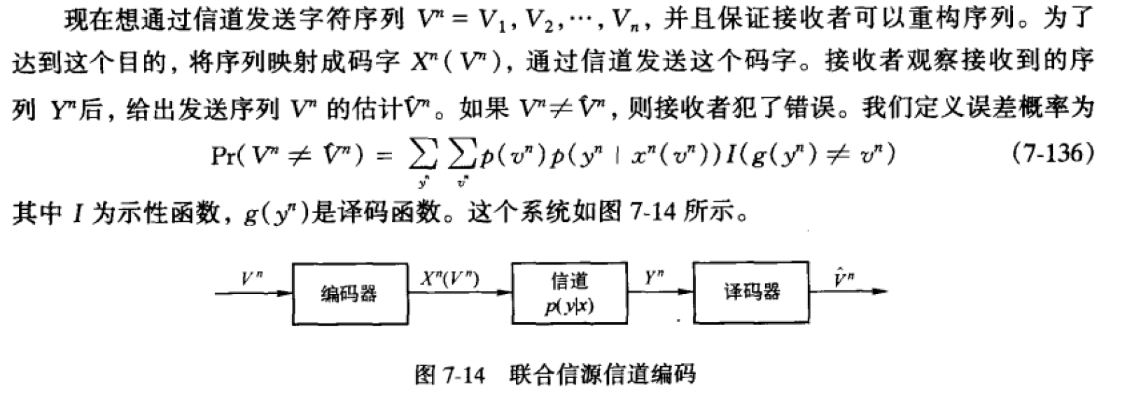
- 对于有限字母表信源\(\mathcal{V}\),如果满足AEP(序列各个时间步iid),以及\(H(\mathcal{V})< C\)
- 那么存在
信源-信道编码使得\(\text{Pr}(\hat{V^{(n)}} \neq V^{(n)})\to 0\) - 反之,大于信道容量,则无法达到任意低的错误概率
在信道容量当中常用的费诺不等式的形式
\[\begin{align*} H(V^{(n)}|\hat{V^{(n)}}) &\leq 1 + \text{Pr}(V^{(n)} <= V^{(n)}) \log |\mathcal{V^{(n)}}| \\&\overset{\text{log}}{\leq} 1 + \text{Pr}(V^{(n)} <= V^{(n)}) \boldsymbol{n} \log |\mathcal{V}| \end{align*}\]
能够通过信道传输平稳遇历信源当且仅当\(H(\mathcal{X}) < C\)
数据压缩与数据传输的关系
-
数据压缩的熵界
- 最优唯一可译码/前缀码长度\(L\in [H,H+1)\)
- 基于AEP
-
信道容量
- 信道容量 = 最大可达码率
- 基于联合AEP
-
信源信道分离定理
- 熵率<码率,\(P_{e}^{n} \to 0\)
- 基于费诺不等式对于误差概率的估计以及数据处理不等式
本文来自博客园,作者:ZXYFrank,转载请注明原文链接:https://www.cnblogs.com/zxyfrank/p/16414515.html



