信息论 二元离散熵的导数
\[(p\log_{2}p)' = \log_{2}p + p \frac{1}{\ln 2}\frac{1}{p} = \frac{\ln p+1}{\ln 2}
\]
\[\begin{align*}
H'(p) &= -\frac{1}{\ln 2}(\ln p + 1 -\ln(1-p) -1)
\\&=-\frac{1}{\ln 2}(\ln \frac{p}{1-p})
\\&=-\log_{2}\frac{p}{1-p}
\\&=\log_{2}\frac{1-p}{p}
\end{align*}\]
\[H'(f(p)) = \boldsymbol{f'(p)}\log_{2}\frac{1-f(p)}{f(p)}
\]
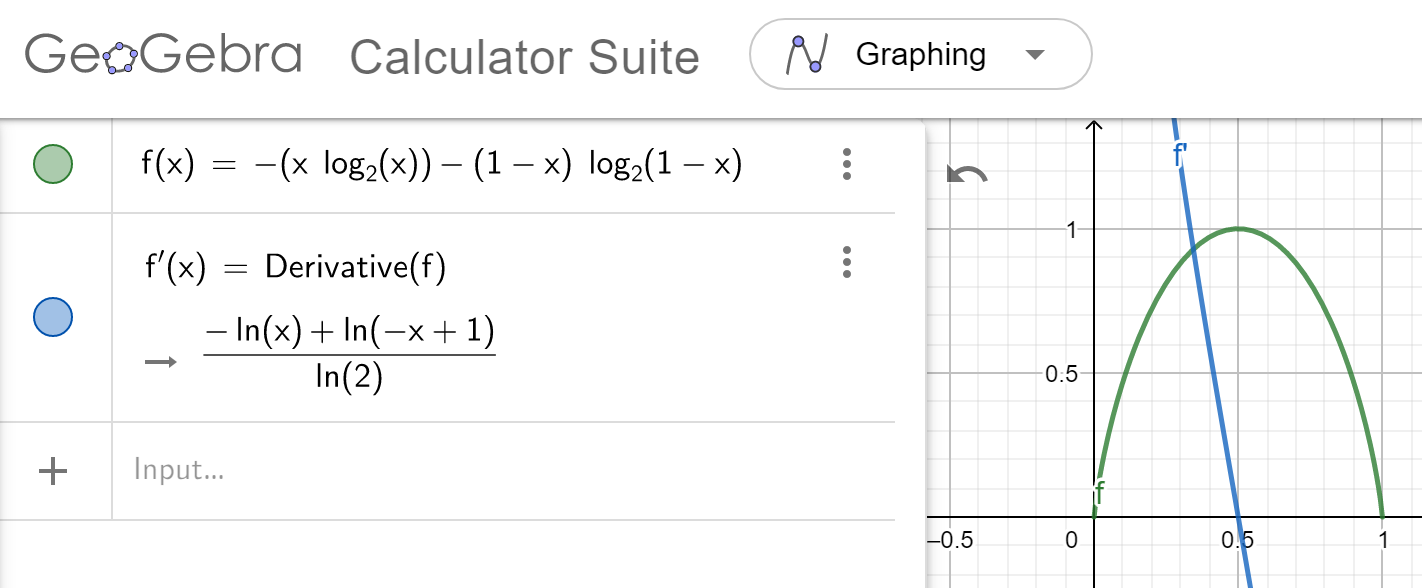
本博文本意在于记录个人的思考与经验,部分博文采用英语写作,可能影响可读性,请见谅
本文来自博客园,作者:ZXYFrank,转载请注明原文链接:https://www.cnblogs.com/zxyfrank/p/16404455.html

