极大似然估计和最大后验估计的关系（机器学习视角）

TL;DR

聊一聊机器学习的MLE和MAP：最大似然估计和最大后验估计 - 夏飞的文章 - 知乎

• 频率学派 - Frequentist - Maximum Likelihood Estimation (MLE，最大似然估计)
  • 世界是确定的，概率客观存在，需要做的就是找到置信区间
• 贝叶斯学派 - Bayesian - Maximum A Posteriori (MAP，最大后验估计)
  • 世界是变化的，需要根据观察调整预判

MAE ≈ MLE + Prior

• 交叉熵 ≈ MLE
• 正态先验MAE ≈ L2正则化

MLE 最大似然估计

样本X = (x1,x2,…,x_n) 服从潜在的独立同分布(iid)

\[\hat{\theta}_{MLE} = \underset{\theta}{\operatorname{\arg\max}} \ P(X;\theta) =\underset{\theta}{\operatorname{\arg\min}} -\sum\log P(x_i;\theta)\\ \]

最大似然估计找出使得当前样本出现概率最大的参数分布，即在似然函数上取极值点

什么是似然

\[L(\theta|X) = f(x;\theta) \]

似然函数在 θ点 数值上等于在 θ点 取得样本的概率密度

最小化交叉熵 = （广义）伯努利分布极大似然估计

简单的交叉熵，你真的懂了吗？ - 蔡杰的文章 - 知乎

相对熵

\[\begin{align} D_{KL}(P||Q) & = \sum P(x_i) \log\frac{P(x_i)}{Q(x_i)} = \sum P(x_i) \log{P(x_i)} - \sum P(x_i) \log{Q(x_i)} \\ & = -H(P) + H(P,Q) \end{align} \]

机器学习当中的交叉熵，H代表 Entropy

\[\text{CrossEntropy} = -\sum_{i = 1}^{n}label_i \cdot\log(score_i) \]

最小化交叉熵损失与极大似然 - Mr.陈同学的文章 - 知乎

MAP 最大后验估计

\[P(\theta|X) = P(\theta) \frac{P(X;\theta)}{P(X)} \]

P(X)与theta 无关，不予考虑

\[\hat{\theta}_{MLE} = \underset{\theta}{\operatorname{\arg\max}}(\log P(\theta) + \log P(X;\theta)) = \underset{\theta}{\operatorname{\arg\min}} (-\log P(X;\theta)- \log P(\theta)) \]

MAP仅仅比MLE在目标函数上多了一个先验分布

MAP ≈ 正则化

假定先验是一个高斯分布，即

注意，先验的分布是theta 的分布

那么， 。

至此，一件神奇的事情发生了 -- 在MAP中使用一个高斯分布的先验等价于在MLE中采用L2的regularizaton！

聊一聊机器学习的MLE和MAP：最大似然估计和最大后验估计 - 夏飞的文章 - 知乎

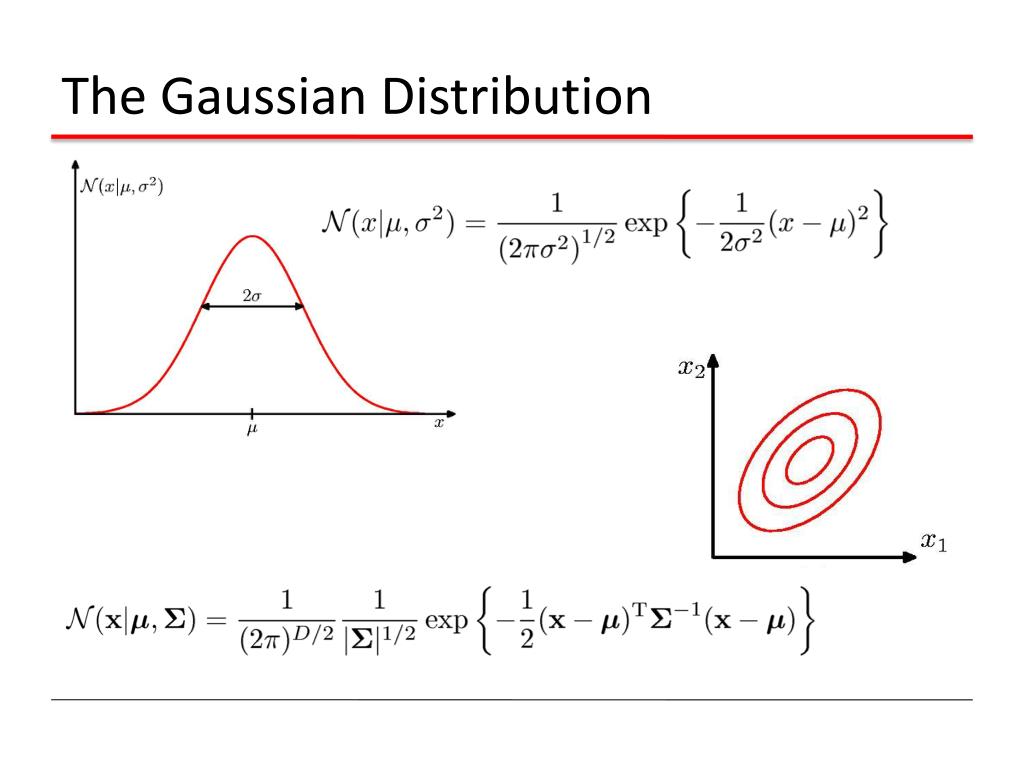
更一般地，假如参数分布不是以0为中心的

\[P(\theta) = N(\theta|\mu,\sigma^2)\\ \log P(\theta) = \text{const} + (\theta -\mu)^2 \]

其本质是优化一个(\theta -\mu)^2MSE