DSA 2020 8.1-8.10
8.1
PAT dfs+dijkstra 重做
// PAT 1018
#include<stdio.h>
#include<vector>
#include<map>
#include<algorithm>
using namespace std;
const int N = 600;
const int INF = 0x3f3f3f3f;
const int ddd = 0;
//const int ddd = 1;
int w[N][N];
int v[N];
int n,m,c,t;
vector<int >pre[N];
bool vis[N];
int dis[N];
vector<int > path;
vector<int > temppath;
int ans = INF;
int minneed = INF;
int minhas = -INF;
void dij(){
for(int i = 0;i<=n;i++){
dis[i] = INF;
}
dis[0] = 0;
for(int i = 0;i<=n;i++){
int k = -7;
int _min = INF;
for(int i = 0;i<=n;i++){
if(!vis[i]&&dis[i]<_min){
_min = dis[i];
k = i;
}
}
vis[k] = 1;
for(int i = 0;i<=n;i++){
if(dis[k]+w[k][i]==dis[i]){
pre[i].push_back(k);
}else if(dis[k]+w[k][i]<dis[i]){
dis[i] = dis[k]+w[k][i];
vector<int >().swap(pre[i]);
pre[i].push_back(k);
}
}
}
}
void dfs(int cur){
if(ddd)printf("%d\n",cur);
temppath.push_back(cur);
if(cur == 0){
int has = 0;
int need = 0;
for(int i = temppath.size()-1;i>=0;i--){
// 遍历这条路径
int at = temppath[i];
if(v[at]<0){
if(has > -v[at]){
// 注意是负数
has += v[at];
}else{
need += -v[at] - has;
has = 0;
}
if(need<minneed){
minneed = minneed;
}
}else if(v[at] >=0){
has += v[at];
}
if(ddd)printf("\tv[at] = %d has = %d need = %d\n",v[at],has,need);
}
// 遍历路径结束
if(need < minneed){
path = temppath;
minneed = need;
minhas = has;
} else if(need == minneed && has < minhas){
// 第二标尺
path = temppath;
minhas = has;
}
}
for(int i = 0;i<pre[cur].size();i++){
dfs(pre[cur][i]);
}
temppath.pop_back();
}
int main(){
scanf("%d %d %d %d",&c,&n,&t,&m);
v[0] = 0;
for(int i = 1;i<=n;i++){
scanf("%d",&v[i]);
v[i] = v[i] - c/2;
}
for(int i = 0;i<N;i++){
for(int j = 0;j<N;j++){
// w[i][j] = -3;
w[i][j] = INF;
}
}
for(int i = 0;i<m;i++){
int u,v,ww;
scanf("%d %d %d",&u,&v,&ww);
w[u][v] = w[v][u] = ww;
}
dij();
dfs(t);
// 输出
printf("%d ",minneed);
for(int i = path.size()-1;i>=1;i--){
printf("%d->",path[i]);
}
printf("%d ",path[0]);
printf("%d",minhas);
return 0;
}
检查出的错误
need += -v[at] - has;之前写成了need = -v[at] - has;忘记累加了for(int i = path.size()-1;i>=1;i++)- 命名不规范,身体的时候就要看好是
max还是min
8.2
正则表达式匹配
class Solution {
public:
string _s;
string _p;
bool match(int ii ,int jj){
// printf("%s\n%s\n",_s.c_str(),_p.c_str());
return (_p[jj] == '.' || _s[ii] == _p[jj]) && ii!=0;
}
bool isMatch(string s, string p) {
int lens = s.size();
int lenp = p.size();
s.insert(0,"#");
p.insert(0,"#");
_s = s;
_p = p;
vector<vector<int > > dp(lens+10,vector<int >(lenp+10,false));
dp[0][0] = true;
// 注意这里的循环
for(int i = 0;i<=lens;i++){
for(int j = 0;j<=lenp;j++){
// 不要害怕越界
if(i == 0&& j == 0)continue;
// 应该把匹配写成一个函数,避免越界问题
// if(s[i] == p[j] || p[j] == '.'){
if(match(i,j)){
if(i>=1 && j>=1)dp[i][j] = dp[i-1][j-1];
}
else{
// 特判
if(p[j] == '*'){
// if(j>0 && (s[i] == p[j-1] || p[j-1] == '.')){
if(j>0 && match(i,j-1)){
// 匹配或者不匹配都行
// 重点理解
if(i>=1)dp[i][j] = dp[i-1][j];
if(j>=2)dp[i][j] |= dp[i][j-2];
}else{
if(j>=2)dp[i][j] = dp[i][j-2];
}
}else{
dp[i][j] = false;
}
}
}
}
return dp[lens][lenp];
}
};
8.3
编辑距离
一遍过😆
// 编辑距离
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int N = 1000 +100;
int dp[N][N];
int n;
char s1[N];
char s2[N];
int n1,n2;
void show(){
for(int i = 0;i<=n1;i++){
for(int j = 0;j<=n2;j++){
printf("%3d",dp[i][j]);
}
printf("\n");
}
}
int main(){
int nn;
scanf("%d",&nn);
while(nn--){
s1[0] = s2[0] = '#';
scanf("%s",s1+1);
scanf("%s",s2+1);
//
n1 = strlen(s1+1);
n2 = strlen(s2+1);
for(int i = 0;i<=n1;i++){
dp[i][0] = i;
}
for(int j = 0;j<=n2;j++){
dp[0][j] = j;
}
//
for(int i = 1;i<=n1;i++){
for(int j = 1;j<=n2;j++){
if(s1[i] == s2[j]){
// 相等
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = min(dp[i-1][j-1]+1,min(dp[i][j-1]+1,dp[i-1][j]+1));
}
}
}
// show();
printf("%d\n",dp[n1][n2]);
}
return 0;
}
取得突破的关键点是打印出来了dp矩阵
kitten->sitting的样例当中发现 dp[6][6]=2但是dp[6][7] = 7
字符相等时,这个位置自然不必做多余的交换,因此有 dp[i][j] = dp[i-1][j-1]
而不相等时,就会出现多种选择
abc->abe对应dp[i-1][j-1]+1,即ab->ab+1(替换)ac->ace对应dp[i][j-1]+1,即ac->ac+1(增加)abc->ab对应dp[i-1][j]+1,即ab->ab+1(删除)
8.4
ACM 环LCS(二进制枚举)
第一次做这样的题目
substr的用法- 发现的错误:二进制枚举
非空子集,应该是
for(int i = 1;i<(1<<l);i++){
不是for(int i = 1;i<=(1<<l);i++){
比如 l = 2
1<<2 = 4 = (100)_2,枚举
2^n-1个数,每一个都利用位运算if(i&(1<<j))考察所有位000,001,010,011
若写成
i<=(1<<l),则就是有包括了 100, 后两位皆是0
// ACM Tomb Raider
#include<map>
#include<vector>
#include<string>
#include<iostream>
#include<stdio.h>
#include<algorithm>
using namespace std;
map<string, int> all,vis;
vector<string> v;
string temp,ss;
void ll(int ii){
// loop
ss = temp.substr(ii);
ss += temp.substr(0,ii);
}
void solve(){
int l = ss.size();
string temps;
for(int i = 1;i<(1<<l);i++){
temps.clear();
for(int j = 0;j<l;j++){
// 对每一位进行考察
if(i&(1<<j)){
temps += ss[j];
}
}
// 同一个
if(vis[temps] == 0 ){
all[temps]++;
vis[temps] = 1;
}
}
}
bool cmp(string s1,string s2){
if(s1.size() != s2.size())return s1.size() > s2.size();
else return s1<s2;
}
int main(){
int nn;
while(scanf("%d",&nn)!=EOF){
vis.clear();
all.clear();
vector<string>().swap(v);
for(int i = 0;i<nn;i++){
cin >> temp;
int lens = temp.size();
// 拆环
for(int j = 0;j <lens;j++){
ll(j);
// ss 是拆环的结果
solve();
}
vis.clear();
}
map<string ,int >::iterator iter;
for(iter = all.begin();iter!=all.end();iter++){
if(iter->second == nn){
// printf("*** %s\n",iter->first.c_str());
v.push_back(iter->first);
}
}
if(v.size() == 0){
printf("0\n");
}else{
sort(v.begin(),v.end(),cmp);
// printf("%s\n",v.begin()->c_str());
printf("%s\n",v[0].c_str());
}
}
}
8.5
打家劫舍 III
类似于“没有上司的舞会”
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int INF = 0x3f3f3f3f;
int tot;
int tott;
int tra(TreeNode * root,vector<vector<int >> & dp){
int l = INF;
int r = INF;
int l0,l1,r0,r1;
int cur = tot++;
dp[0].push_back(0);
dp[1].push_back(1);
if(root->left!=NULL){
l = tra(root->left,dp);
}
if(root->right!=NULL){
r = tra(root->right,dp);
}
if(root->left!=NULL){
l0 = dp[0][l];
l1 = dp[1][l];
}else{
l0 = 0;
l1 = 0;
}
if(root->right!=NULL){
r0 = dp[0][r];
r1 = dp[1][r];
}else{
r0 = 0;
r1 = 0;
}
dp[0][cur] = max(l0,l1)+max(r0,r1);
dp[1][cur] = l0+r0 + root->val;
return cur;
}
int rob(TreeNode* root) {
// 如何在不改变树的结构的情况下进行数据的处理
if(root == NULL){
return 0;
}
vector<vector<int >> dp;
dp.push_back(vector<int >());
dp.push_back(vector<int >());
tra(root,dp);
return max(dp[0][0],dp[1][0]);
}
};
如何建立全局的dp表?我想到的方法是返回左右的数组下标作为索引,而数组的开辟通过每个dfs函数的入口int cur = tot++;实现。
更好的方法是,因为每一个节点的值只有两种情况
- 如果该点不取,
return max(l,r) - 如果该点取,
return val+所有孙辈的最大值
其实每一个点在决策时只需要最大值这一个,而二叉树的结构保证了孙辈个数 <=4
因此有更方便的解法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
// 每个节点都需要在返回自己的最大值情况下,同时返回孙辈的最大值
int rrob(TreeNode * root,int & maxl,int & maxr){
if(root == NULL){
return 0;
}
// 孩子,返回的时候顺便帮我问一下孙辈的情况,我自己做决定
int ll = 0,lr = 0,rl = 0,rr = 0;
maxl = rrob(root->left,ll,lr);
maxr = rrob(root->right,rl,rr);
// 因此,这里也可以写作
return max(root->val + ll + lr + rl + rr, maxl + maxr);
// return int[3]{
// max(root->val + ll + lr + rl + rr, maxl + maxr),
// maxl
// maxr};
}
int rob(TreeNode* root) {
int l = 0,r = 0;
return rrob(root,l,r);
}
};
8.6
回文对
BF 算法可以得到 O(n^2m)的复杂度
如何避免n过大带来的影响,可以考虑在遍历到每一个字符串的时候,采用hasing,不去考察其他的字符串,直接通过预处理保存所有的字符串信息
空间复杂度相对较大,需要存储所有反向子串,O(nm)
这里有一个题解很有意思。因为在stl的hashing 函数当中不支持 hasing 的拼接
class Solution {
public:
set<vector<int>> ans;
map<string,int > rsi;
string temp;
vector<vector<int>> aans;
map<string,int >::iterator it;
int find(string s,int i ,int j){
// if(i>j) return -1;
if(i>j) it = rsi.find("");
it = rsi.find(s.substr(i,j-i+1));
if(it == rsi.end())return -1;
else return it->second;
}
bool mir(string s, int b, int e){
// if(b>e)return false;
// if(s.size() == 0 || b = e)return true;
if(s.size() == 0 || b >= e)return true;
for(int i = 0;i<=(e-b)/2;i++){
if(s[b+i]!=s[e-i])return false;
}
return true;
}
vector<vector<int>> palindromePairs(vector<string>& words) {
int n = words.size();
for(int i = 0;i<words.size();i++){
temp.assign(words[i].rbegin(),words[i].rend());
rsi[temp] = i;
}
for(int i = 0;i<n;i++){
string s;
// s.assign(words[i].rbegin(),words[i].rend());
s = words[i];
int m = s.size();
for(int j = 0;j<m;j++){
if(mir(s,j,m-1)){
// 左侧
int r = find(s,0,j-1);
if(r != -1 && r != i){
ans.insert({i,r});
}
}
// if(mir(s,0,j-1)){
if(mir(s,0,j-1)){
// 右侧
int l = find(s,j,m-1);
if(l != -1 && l != i){
ans.insert({l,i});
}
}
}
}
aans.assign(ans.begin(),ans.end());
return aans;
}
};
输入:
["a",""]
输出:
[[0,1]]
预期结果:
[[0,1],[1,0]]
明天继续研究吧
😆哈哈,十一点半做出来了!虽然本身以为优化了题解但是没有hhh,但是还是自己发现了问题!
class Solution {
public:
set<vector<int>> ans;
map<string,int > rsi;
string temp;
vector<vector<int>> aans;
map<string,int >::iterator it;
int find(string s,int i ,int l){
// if(i>j) return -1;
it = rsi.find(s.substr(i,l));
if(it == rsi.end())return -1;
else return it->second;
}
bool mir(string s, int b, int l){
// if(b>e)return false;
// if(s.size() == 0 || b = e)return true;
if(l == 0 || s.size() == 0)return true;
int e = b+l-1;
for(int i = 0;i<=(e-b)/2;i++){
if(s[b+i]!=s[e-i])return false;
}
return true;
}
vector<vector<int>> palindromePairs(vector<string>& words) {
int n = words.size();
for(int i = 0;i<words.size();i++){
temp.assign(words[i].rbegin(),words[i].rend());
rsi[temp] = i;
}
for(int i = 0;i<n;i++){
string s = words[i];
int m = s.size();
for(int l = 0;l<=m;l++){
if(mir(s,l,m-l)){
// 左侧
// 语义规范
int ri = find(s,0,l);
if(ri != -1 && ri != i){
ans.insert({i,ri});
}
}
if(mir(s,0,m-l)){
// 右侧
int li = find(s,m-l,l);
if(li != -1 && li != i){
ans.insert({li,i});
}
}
}
}
aans.assign(ans.begin(),ans.end());
return aans;
}
};
tricks
- 采用set 去重
- 采用枚举区间长度的方法
begin & length,解决枚举空串的问题
8.7
二分查找——有序数组的中位数
思想
- 二分查找
- 交叉小于——将数组的一边看成整体
写了一上午,虽然看了题解,但是还是想了很久
还是那个小问题,如何如何解决空字符的问题,其实加哨兵就可以了,但是这里如果加哨兵就会影响总体的时间复杂度
class Solution {
public:
int INF = 0x3f3f3f3f;
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
if(nums2.size()<nums1.size()){
nums1.swap(nums2);
}
int len1 = nums1.size();
int len2 = nums2.size();
int nleft = (len1 + len2 + 1)/2;
// 枚举的是短序列左侧区间的字符数量
int l = 0;
int r = len1;
while(l<r){
int mid = (l+r)/2;
int i = mid, j = nleft - mid;
printf("l = %d r = %d mid = %d j = %d nleft = %d\n",l,r,mid,j,nleft);
int l1 = i == 0?-INF:nums1[i-1];
int r1 = i == len1?INF:nums1[i];
int l2 = j == 0?-INF:nums2[j-1];
int r2 = j == len2?INF:nums2[j];
printf("\tl1 = %d r1 = %d\n\tl2 = %d r2 = %d\n",l1,r1,l2,r2);
// if(nums1[mid-1]>nums2[j] || nums2[j-1] > nums1[mid]){
// if(l1>nums2[j] || l2>nums1[mid]){
if(l1>r2 || l2<r1){
r = mid;
}else{
l = mid + 1;
}
}
int i = l,j = nleft - i;
int l1 = i == 0?-INF:nums1[i-1];
int r1 = i == len1?INF:nums1[i];
int l2 = j == 0?-INF:nums2[j-1];
int r2 = j == len2?INF:nums2[j];
if((len1 + len2) % 2== 1){
return max(l1,l2);
}else{
return (max(l1,l2) + min(r1,r2))*1.0/2;
}
}
};
-
我自己一般是这样写的,由于整数除法向下取整,所以左边界向右扩展可以保证区间长度递减
int l = 0, r = len; while(l<r){ int mid = (l+r)/2; if(...) l = mid+1; else r = mid; }题解当中使用了这样的二分查找
while(l < r){ int i = (l + r + 1)/2; // 当进行到[3,4]这样的区间时,取右侧端点作为 mid int j = total - i; // 这种情况下不会出现 i = 0 的情况 // 只有 i = 1时,可能出现 r = 1-1 = 0;从而得到[0,0]区间的情况 if(nums1[i-1] > nums2[j]) r = i-1; else l = i; }
为什么只有一个判断条件呢?
我写的是
l1>r2 || l2<r1
情况 动作 l1>r2 && l2 > r1 不可能出现! l1>r2 && l2 <=r1 i-=? l1<=2 && l2 > r1 i+=? l1<=r2 && l2 <= r1 满足条件 按道理来说,我的这个写法是错误的
应该是写明白才好
if(l1>r2 && l2<=r1){ r = mid; }else if(l1<=r2 && l2>r1){ l = mid + 1; }else if(l1<=r2 && l2<=r1){ l = mid; break; }
重做一下这道题目
两个有序数组寻找第 K 小元素
class Solution {
public:
int INF = 0x3f3f3f3f;
int findk(vector<int>& nums1, vector<int>& nums2,int k){
int len1 = nums1.size();
int len2 = nums2.size();
int base1 = 0, base2 = 0;
int cur1 = 0, cur2 = 0;
while(1){
cur1 = base1 + k/2 - 1;
cur2 = base2 + k/2 - 1;
printf("cur1 = %d cur2 =%d k = %d\n",cur1,cur2,k);
if(base1 > len1 - 1){
return nums2[base2 + k - 1];
}
if(base2 > len2 - 1){
return nums1[base1 + k - 1];
}
if(k == 1){
return min(nums1[base1],nums2[base2]);
}
cur1 = min(len1 - 1,base1 + k/2 - 1);
cur2 = min(len2 - 1,base2 + k/2 - 1);
if(nums1[cur1] < nums2[cur2]){
k -= cur1 - base1 +1;
base1 = cur1 + 1;
}else{
k -= cur2 - base2 +1;
base2 = cur2 + 1;
}
}
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int l1 = nums1.size();
int l2 = nums2.size();
int k1 = (l1+l2+1)/2;
int k2 = (l1+l2+2)/2;
if((l1+l2)%2 == 0){
return double(findk(nums1,nums2,k1) + findk(nums1,nums2,k2))*1.0/2;
}else{
return findk(nums1,nums2,k1);
}
}
};
k1 = (l1+l2+1)/2; k2 = (l1+l2+2)/2
8.8
恢复二叉树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<TreeNode* > v;
void dfs(TreeNode * node){
if(node->left) dfs(node->left);
v.push_back(node);
if(node->right) dfs(node->right);
}
void recoverTree(TreeNode* root) {
dfs(root);
vector<int > ans;
for(int i = 0;i<v.size()-1;i++){
if(v[i]->val>v[i+1]->val){
ans.push_back(i);
break;
}
}
for(int i = v.size()-1;i>=1;i--){
if(v[i]->val<v[i-1]->val){
ans.push_back(i);
break;
}
}
if(ans.size() == 1){
swap(v[ans[0]]->val,v[ans[0]-1]->val);
}else if(ans.size() == 2){
swap(v[ans[0]]->val,v[ans[1]]->val);
}
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int INF = 0x3f3f3f3f;
TreeNode* pred;
vector<TreeNode * > ans,anspred;
void ldr(TreeNode * root){
// Morris 遍历
TreeNode * cur = root, * pred = nullptr;
while(cur != nullptr){
printf("%d\n",cur->val);
if(cur->left== nullptr){
// 左侧子树访问完毕,访问cur 节点
if(pred!=nullptr && cur->val < pred->val){
ans.push_back(cur);
anspred.push_back(pred);
}
pred = cur;
cur = cur->right;
}else{
TreeNode * lrm = cur->left;
// 寻找左侧子树最优节点(pred)
while(lrm->right != nullptr && lrm->right != cur) lrm = lrm->right;
if(lrm -> right == nullptr){
lrm->right = cur;
cur = cur->left;
}else if(lrm == nullptr || lrm->right == cur){
// 访问一个没有左侧节点的子节点cur(最左下节点)
if(pred!=nullptr && cur->val < pred->val){
ans.push_back(cur);
anspred.push_back(pred);
}
lrm->right = nullptr;
pred = cur;
cur = cur->right;
}
}
}
}
void recoverTree(TreeNode* root) {
ldr(root);
if(ans.size() == 1){
swap(ans[0]->val,anspred[0]->val);
}else if(ans.size() == 2){
swap(anspred[0]->val,ans[1]->val);
}
}
};
8.9
复原IP地址
解决不可以连续读零的问题 这一个测试用例 "010010"
-
设置标志位,表明读到了一个零
-
if(temp == 0) return; if(temp == INF) temp = 0;// 一个新数字的开始
class Solution {
public:
vector<string> ans;
int len;
int INF = 0x3f3f3f3f;
vector<int> temps;
string getans(){
string r;
if(temps.size() == 4){
for(int i = 0;i<3;i++){
r += to_string(temps[i])+".";
}
r+= to_string(temps[3]);
}
return r;
}
void dfs(string &s, int num, int cur,int temp){
if(cur == len ^ num ==4) return;
else if(num == 4 && cur == len){
ans.push_back(getans());
return;
}
if(temp == 0) return;
if(temp == INF) temp = 0;// 一个新数字的开始
int newtemp = temp* 10 + s[cur] -'0';
printf("%d\n",newtemp);
if(newtemp > 255)return ;
if(newtemp<=255){
temps.push_back(newtemp);
dfs(s,num+1,cur+1,INF);
temps.pop_back();
}
dfs(s,num,cur+1,newtemp);
}
vector<string> restoreIpAddresses(string s) {
len = s.size();
dfs(s,0,0,INF);
return ans;
}
};
最长有效括号子串
验证一个子串是不是括号需要 O(n)的时间
- 计数器
- 栈
- 动态规划
这有一步很巧妙的处理:init: st.push(-1);
这样相当于
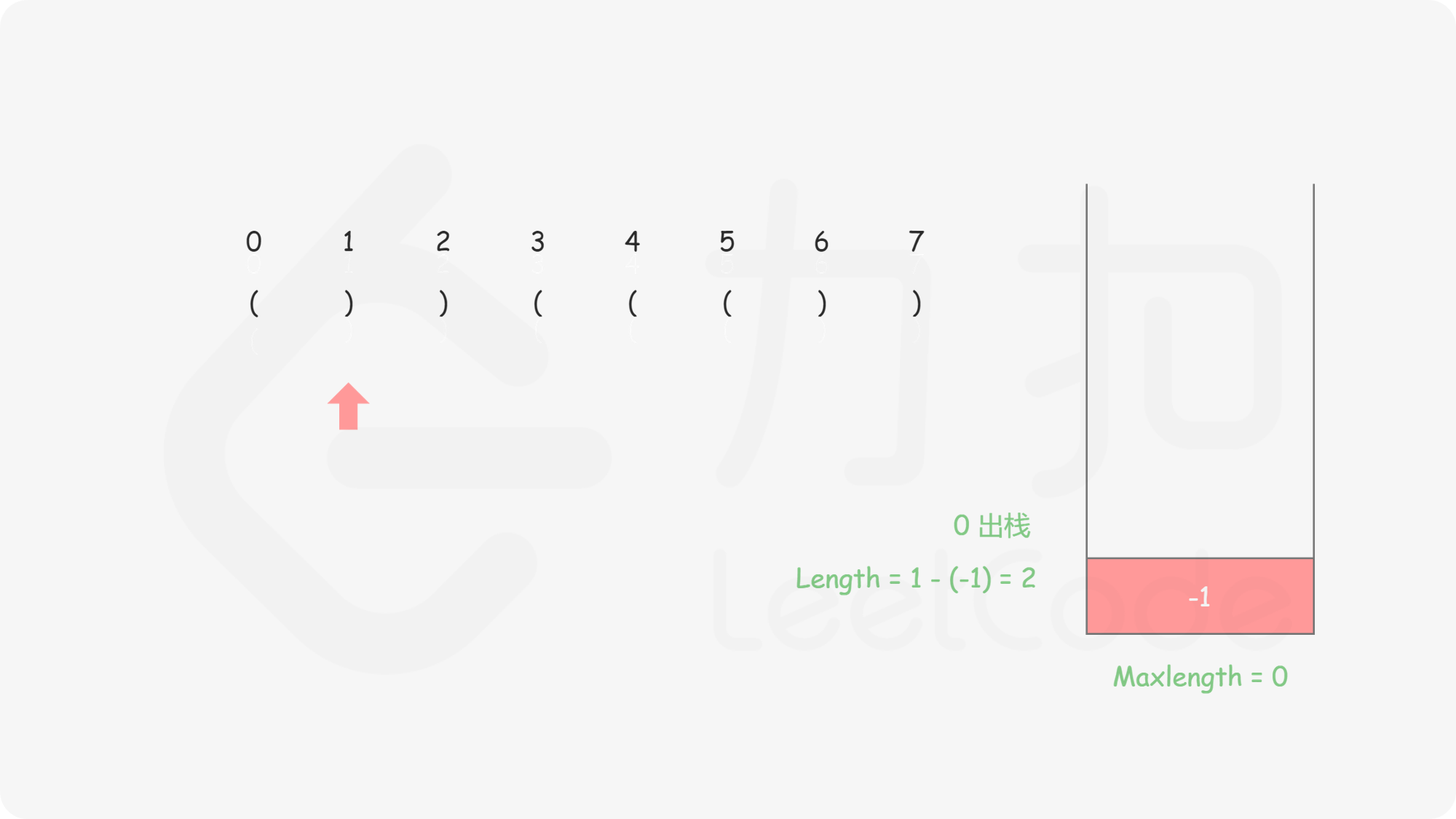
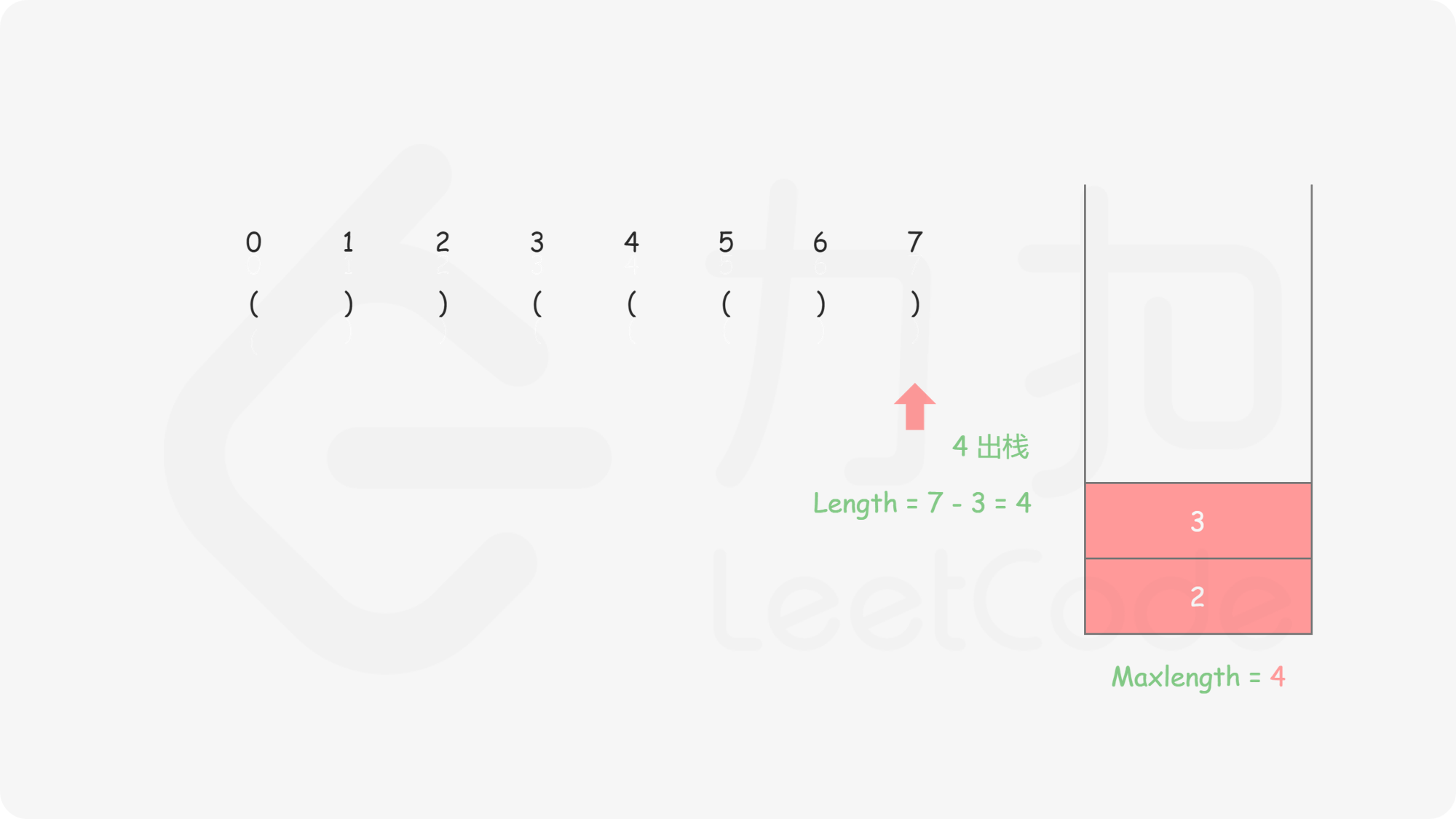
和栈空不一样,这里每一个合法括号串匹配完成后都可以找到一个起始位置 st.top()
class Solution {
public:
stack<int > st;
int ans;
int longestValidParentheses(string s) {
int len = s.size();
int cur = 0;
st.push(-1);
while(cur < len){
if(s[cur] == '('){
st.push(cur);
}
else if(s[cur] == ')'){
if(st.empty()){
st.push(cur);
}else{
st.pop();
if(st.empty()){
// 更新连续可行串起点
st.push(cur);
}else{
// 更新答案
ans = max(ans,cur - st.top());
}
}
}
cur ++;
}
return ans;
}
};
8.10
重做正则表达式匹配
阶段总结
-
动态规划
正则表达式匹配,编辑距离,打家劫舍Ⅲ(单点递归)、最长有效括号子串
-
搜索
PAT 1018,复原IP
-
二分查找
有序数组的中位数
-
二进制枚举
下一阶段的任务:十天刷完剑指offer
本文来自博客园,作者:ZXYFrank,转载请注明原文链接:https://www.cnblogs.com/zxyfrank/p/13938899.html

