LeetCode 精选21-38 until 9-29
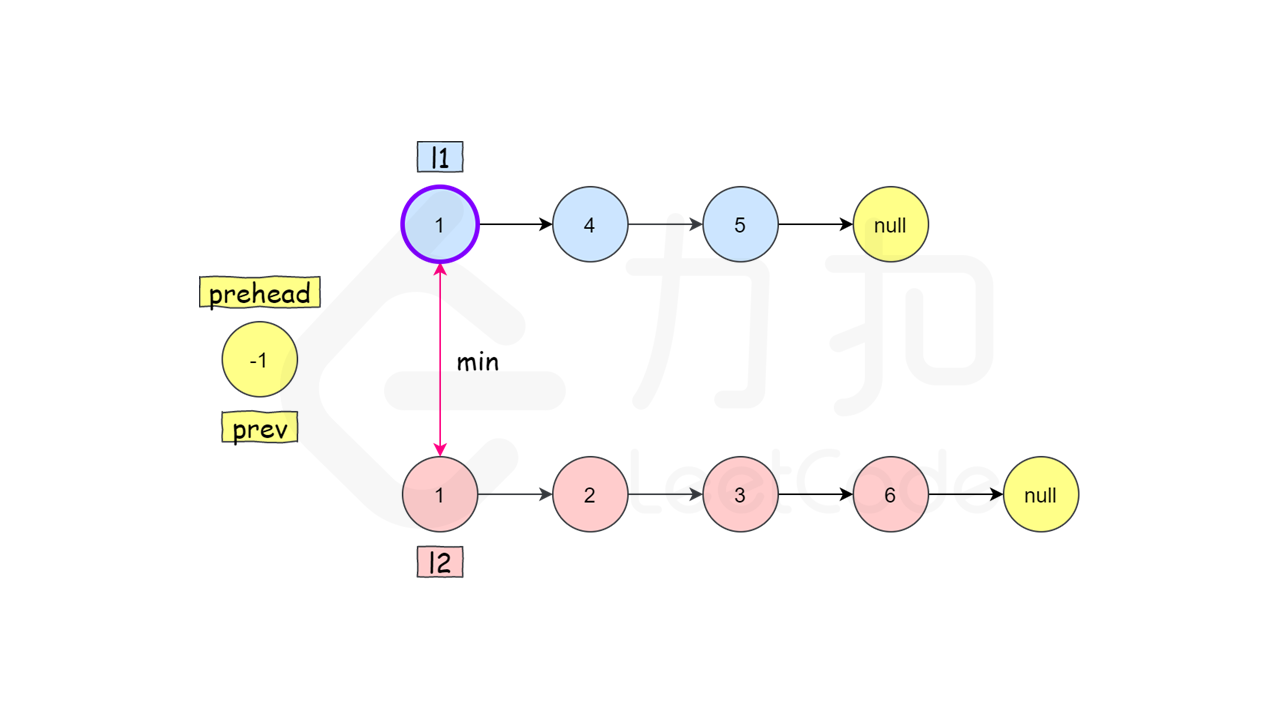
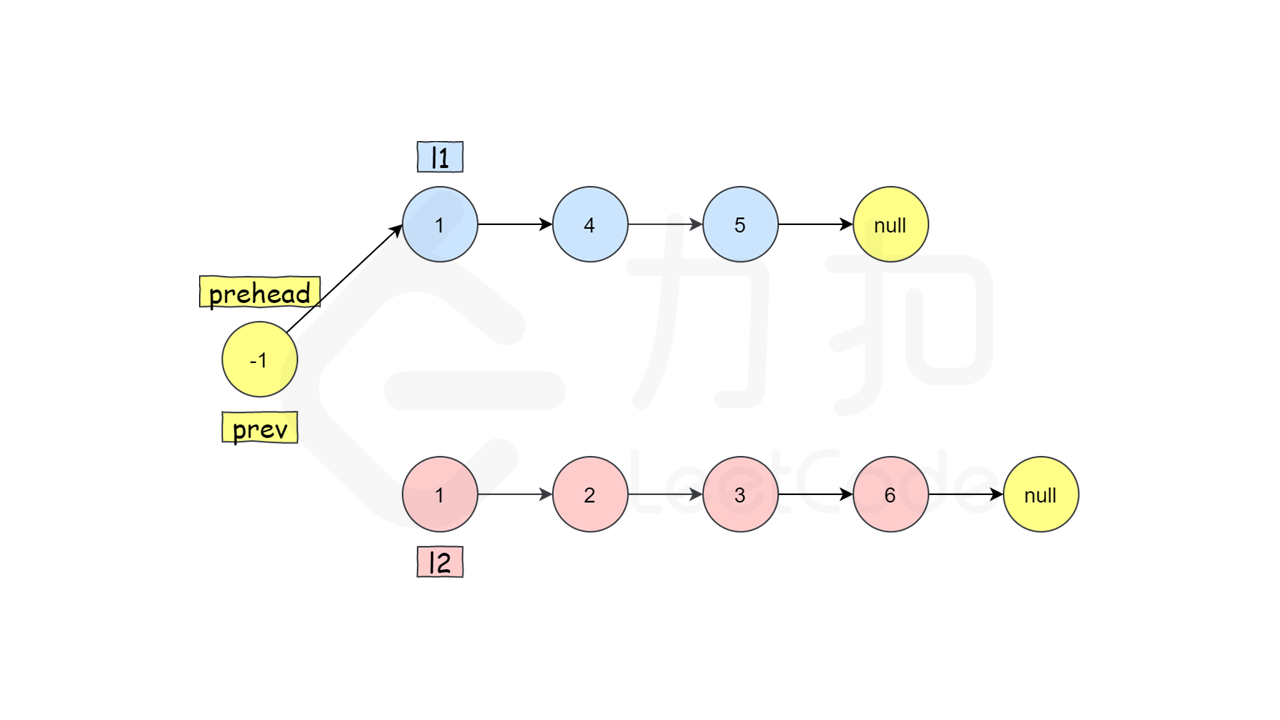
9/17 21. 合并两个有序链表 25min
哨兵节点
ListNode head = new ListNode(-1);
ListNode cur = head;
9/18 22. 括号生成 25 / 60+ min
力扣的模拟面试功能挺好用的哈哈
基本解法:下游去重
class Solution {
ArrayList<String>[] cache;
List<String> ms(int i){
// ex i = 3
if(cache[i]!=null){
return cache[i];
}
ArrayList<String> ans = new ArrayList<String>();
// parallel
for(int j = 1;j <= i / 2;j++){
List<String> left = ms(j);
List<String> right = ms(i - j);
for(String l : left){
for(String r:right){
ans.add(l+r);
ans.add(r+l);
}
}
}
// nested
for(String s : ms(i-1)){
ans.add("("+s+")");
}
cache[i] = ans;
return ans;
}
public List<String> generateParenthesis(int n) {
// init
cache = new ArrayList[100];
cache[0] = new ArrayList<String>();
cache[1] = new ArrayList<String>(){{
add("()");
}};
List<String> ss = ms(n);
Set<String> set = new HashSet<String>();
for(String s : ss){
set.add(s);
}
return new ArrayList<String>(set);
}
}
括号的生成
- 首先,简单的减一而治之是不可行的
class Solution {
public List<String> generateParenthesis(int n) {
if(n == 0)return null;
if(n == 1)return new ArrayList<String>(){{
add("()");
}};
Set<String> ans = new HashSet<String>();
List<String> left = generateParenthesis(n-1);
for(String s : left){
ans.add("("+s+")");
ans.add(s + "()");
ans.add("()" + s);
}
return new ArrayList(ans);
}
}
List<String> left = generateParenthesis(n-1);
2 + 2
(())(()) - > (
())(())
- 太麻烦了
ms(n) = ms(i) + ms(n-i) for i in [1,n-1]?
非递归解法
动态规划
想到动态规划就应该想到
ms (dfs+)
ArrayList<T>[] cache = new ArrrayList[100];
但是这样会导致重复
()()()()() = 1+4? = 2+3?
重复的根源所在——结构相似
- 如果
ms(i)+ms(n-i)与ms(j)+ms(n-j)重复 - ()()() + ()() / () + ()()()()
一定代表出现了子结构
好像也不一定是这样……
如何避免重复
ms(n) = (ms(i)) + ms(n-1-i);
⭐回溯法
class Solution {
char[] ch;
List<String> ans;
void gen(int cur, int leftp, int n){
// cur = 当前位置 leftp = 左侧未关闭括号
// 自由生长,剩余位置不足以关闭括号,自动剪枝
if(leftp < 0 || n - cur < leftp){
return;
}
// 添加答案
if(cur == n && leftp == 0){
ans.add(String.valueOf(ch));
return;
}
// 关闭一个括号
ch[cur] = ')';
gen(cur + 1,leftp - 1,n);
// 或者再开放一个括号
ch[cur] = '(';
gen(cur + 1,leftp + 1,n);
}
public List<String> generateParenthesis(int n) {
ch = new char[n*2];
ans = new ArrayList<String>();
// 最左侧一定是开放的括号
ch[0] = '(';
gen(1,1,n*2);
return ans;
}
}
竟然!
100 %✌
中间隔了两天,打算给20%的余量
9/21 补23. 合并K个升序链表
基本方法:优先级队列
AC
class Solution {
class State implements Comparable<State>{
int val;
ListNode ptr;
public State(int _val,ListNode _ptr){
this.val = _val;
this.ptr = _ptr;
}
public int compareTo(State x){
return this.val - x.val;
}
}
PriorityQueue<State> q = new PriorityQueue<State>();
public ListNode mergeKLists(ListNode[] lists) {
ListNode head = new ListNode(-1);
ListNode tail = head;
// init
for(int i = 0;i<lists.length;i++){
if(lists[i]!=null){
q.offer(new State(lists[i].val,lists[i]));
}
}
while(!q.isEmpty()){
State min = q.poll();
ListNode cur = min.ptr;
tail.next = cur;
tail = tail.next;
cur = cur.next;
if(cur!=null){
q.offer(new State(cur.val,cur));
}
}
return head.next;
}
}
分治:🔍 关注可见域 [l,r]
类似于归并排序,
- mergeSort
- merge
class Solution {
public ListNode merge2(ListNode l1,ListNode l2){
ListNode head = new ListNode(-1);
ListNode tail = head;
while(l1 != null && l2 != null){
if(l1.val < l2.val){
tail.next = l1;
l1 = l1.next;
tail = tail.next;
}else{
tail.next = l2;
l2 = l2.next;
tail = tail.next;
}
}
tail.next = l1 == null ? l2 : l1;
return head.next;
}
public ListNode merge(ListNode[] lists,int b, int e){
if(b > e)return null;
// if(b == e)return lists[0];
if(b == e)return lists[b];
int mid = (b+e)/2;
return merge2(merge(lists,b,mid),merge(lists,mid + 1,e));
}
public ListNode mergeKLists(ListNode[] lists) {
return merge(lists,0,lists.length - 1);
}
}
❗在归并类的方法当中,所有的操作都应该在参数数组的可见域 [l,r] / [b,e]之中进行
// if(b == e)return lists[0]; if(b == e)return lists[b];
100% 💃
9/21 补 26. 删除排序数组中的重复项
SKIPPING
class Solution {
public int removeDuplicates(int[] nums) {
int count = 0;
int cur = 0;
while(cur< nums.length){
count ++;
// skip the duplicates to the first differetnt element
while(cur + 1<nums.length && nums[cur + 1] == nums[cur]){cur++;}
cur ++;
}
// move
cur = 0;
for(int i = 0;i<count;i++){
nums[i] = nums[cur];
while(cur + 1<nums.length && nums[cur + 1] == nums[cur]){cur++;}
cur ++;
}
return count;
}
}
😅多排了一趟
class Solution {
public int removeDuplicates(int[] nums) {
int count = 0;
int cur = 0;
while(cur< nums.length){
// skip the duplicates to the first differetnt element
while(cur + 1<nums.length && nums[cur + 1] == nums[cur]){cur++;}
nums[count ++] = nums[cur ++];
}
return count;
}
}
官方的代码思路非常好,巧妙地利用了快慢指针的概念
快指针始终以慢指针作为参照
public int removeDuplicates(int[] nums) {
if (nums.length == 0) return 0;
int i = 0;
for (int j = 1; j < nums.length; j++) {
if (nums[j] != nums[i]) {
i++;
nums[i] = nums[j];
}
}
return i + 1;
}
做一做简单题可以看到简洁优雅的代码
简洁的思路就应该用简洁的代码实现💃
9/22 28. 实现 strStr() 字符串匹配
KMP 模板
class Solution {
int[] next;
void getNext(String s){
int len = s.length();
next = new int[len + 10];
next[0] = -1;
int j = 0,k = -1;
while(j<len){
if(k == -1 || s.charAt(j) == s.charAt(k))next[++j] = ++k;
else k = next[k];
}
}
public int strStr(String s, String p) {
getNext(p);
int i = 0,j = 0;
int lens = s.length(),lenp = p.length();
while(i < lens && j < lenp){
if(j == -1 || s.charAt(i) == p.charAt(j)){i++;j++;}
else j = next[j];
}
if(j == lenp) return i-lenp;
else return -1;
}
}
9/22 29. 两数相除
class Solution {
public int divide(int dividend, int divisor) {
if(dividend == Integer.MIN_VALUE && divisor == -1){
return Integer.MAX_VALUE;
}
boolean pos = true;
if((dividend > 0) ^ (divisor > 0) == true)pos = false;
int count = 0;
// 转化为正数
dividend = Math.abs(dividend);
divisor = Math.abs(divisor);
while(dividend >= divisor){
count ++;
dividend -= divisor;
}
return pos?count:-count;
}
}
这一个用例没有通过
输入:
-2147483648 1
输出:
0
预期结果:
-2147483648
❗绝对值溢出问题
// 转化为正数
// 这里可能出现问题
dividend = Math.abs(dividend);
divisor = Math.abs(divisor);
转化为负数即可
dividend = -Math.abs(dividend);
divisor = -Math.abs(divisor);
Math.abs(Integer.MIN_VALUE) = Integer.MIN_VALUE
INT_MAX + 1 = INT_MIN
INT_MIN = -INT_MIN
int min = -Integer.MIN_VALUE;
System.out.println(Integer.MIN_VALUE);
System.out.println(min);
// -2147483648
// -2147483648
❗
0xFFFFFFFF = 2147483647
0x1 + 0xFFFFFFFF = 2147483648
[1]000 0000 0000 0000] 最高位因为是符号位,变成了1
系统认定为整数,对应的绝对值为取反加一,即 []111 1111 1111 1111 + 1 = [1]000 0000 0000 0000
绝对值是 INT_MAX,符号位为负
#include<stdio.h>
int main(){
int min = -2147483648;
int max = 2147483647;
int negmax = -max;
int negmin = -min;
printf("%d\n%d\n%d\n%d\n",min,max,negmax,negmin);
int over = 2147483648;
printf("overflow = %d\n",over);
printf("-overflow = %d\n",-over);
printf("overflow + 1 = %d\n",over + 1);
printf("overflow - 1 = %d\n",over - 1);
}
// -2147483648
// 2147483647
// -2147483647
// -2147483648
// overflow = -2147483648
// -overflow = -2147483648
// overflow + 1 = -2147483647
// overflow - 1 = 2147483647
二分解法
❗全部使用负数运算
class Solution {
public int divide(int dividend, int divisor) {
if(dividend == Integer.MIN_VALUE && divisor == -1){
return Integer.MAX_VALUE;
}
boolean pos = true;
int ans = 0;
if((dividend > 0) ^ (divisor > 0) == true)pos = false;
// 转化为正数
dividend = -Math.abs(dividend);
divisor = -Math.abs(divisor);
while(dividend <= divisor){
int count = -1;
int pow = divisor;
while(dividend <= pow << 1){
// 采用移位代替乘法运算
// 无需太过贪婪,避免溢出
// -2147483648 >> 1 = -1073741824
if(pow <= (Integer.MIN_VALUE >> 1)) break;
pow = pow << 1;
count = count << 1;
}
dividend -= pow;
ans += count;
}
return pos?-ans:ans;
}
}
9/23 33. 搜索旋转排序数组20 min
class Solution {
public int getPivot(int[] nums,int l,int r){
if(r == l + 1 && nums[l] > nums[r])return l;
int mid = (l + r) / 2;
if(nums[mid] > nums[r]) return getPivot(nums,mid + 1,r);
else return getPivot(nums,l,mid);
}
public int bs(int[] nums,int tar,int _l,int _r){
int l = _l,r = _r;
while(l<r){
int mid = (l + r) / 2;
if(nums[mid] == tar){
return mid;
}else if(nums[mid] < tar){
l = mid + 1;
}else{
r = mid;
}
}
return -1;
}
public int search(int[] nums, int target) {
int p = getPivot(nums,0,nums.length - 1);
int i1 = bs(nums,target,0,p);
int i2 = bs(nums,target,p+1,nums.length - 1);
if(i1 == -1 && i2 == -1){
return -1;
}else{
return i1 == -1? i2 : i1;
}
}
}
[1]
0
AC
class Solution {
public int getPivot(int[] nums,int l,int r){
if(nums.length == 1)return -1;
if(r == l + 1){
return nums[l] > nums[r] ? l : -1;
}
int mid = (l + r) / 2;
if(nums[mid] > nums[r]) return getPivot(nums,mid,r);
// else return getPivot(nums,l,mid - 1);
else return getPivot(nums,l,mid);
}
public int bs(int[] nums,int tar,int _l,int _r){
int l = _l,r = _r;
while(l<r){
int mid = (l + r) / 2;
if(nums[mid] == tar){
return mid;
}else if(nums[mid] < tar){
l = mid + 1;
}else{
r = mid;
}
}
return nums[l] == tar ? l : -1;
}
public int search(int[] nums, int target) {
int p = getPivot(nums,0,nums.length - 1);
System.out.println(p);
if(p == -1){
return bs(nums,target,0,nums.length - 1);
}
int i1 = bs(nums,target,0,p);
int i2 = bs(nums,target,p+1,nums.length - 1);
if(i1 == -1 && i2 == -1){
return -1;
}else{
return i1 == -1? i2 : i1;
}
}
}
二分法的返回
二分查找的重点总是一个平凡情况 l = r
- 提前找到目标值,可以提前退出(也可以不提前退出,统一在外侧判断,但是这样会影响最好情况下的复杂度)
while退出之后,可能退回到平凡点,需要return a[l] == tar ? l : -1;
162. 寻找峰值
34. 在排序数组中查找元素的第一个和最后一个位置
二分查找的关键行为如何定义?
class Solution {
int bs1(int[] nums,int target){
int l = 0,r = nums.length - 1;
if(r == 0)return nums[0] == target ? 0 : -1;
while(l<r){
int mid = (l + r)/ 2;
if(nums[mid] < target){
l = mid + 1;
}else{
// 向左侧收缩,定义右边界行为
// 其实是在定义等于时的行为
// when geq, right shrinks
r = mid;
}
}
return nums[l] == target ? l : -1;
}
int bs2(int[] nums,int target){
int l = 0,r = nums.length - 1;
if(r == 0)return nums[0] == target ? 0 : -1;
while(l<r){
int mid = (l + r + 1)/ 2;
if(nums[mid] > target){
r = mid - 1;
}else{
// when leq, left shrinks
l = mid;
}
}
return nums[l] == target ? l : -1;
}
public int[] searchRange(int[] nums, int target) {
return nums.length == 0 ? new int[]{-1,-1} : new int[]{bs1(nums,target),bs2(nums,target)};
}
}
取到等号时,可以选择左侧收缩或者右侧收缩,这样可以实现不同的搜索方向
在不相等时,总可以写
mid = (l+r)/2;l = mid + 1; r = mid; // or mid = (l+r+1)/2;l = mid; r = mid - 1;
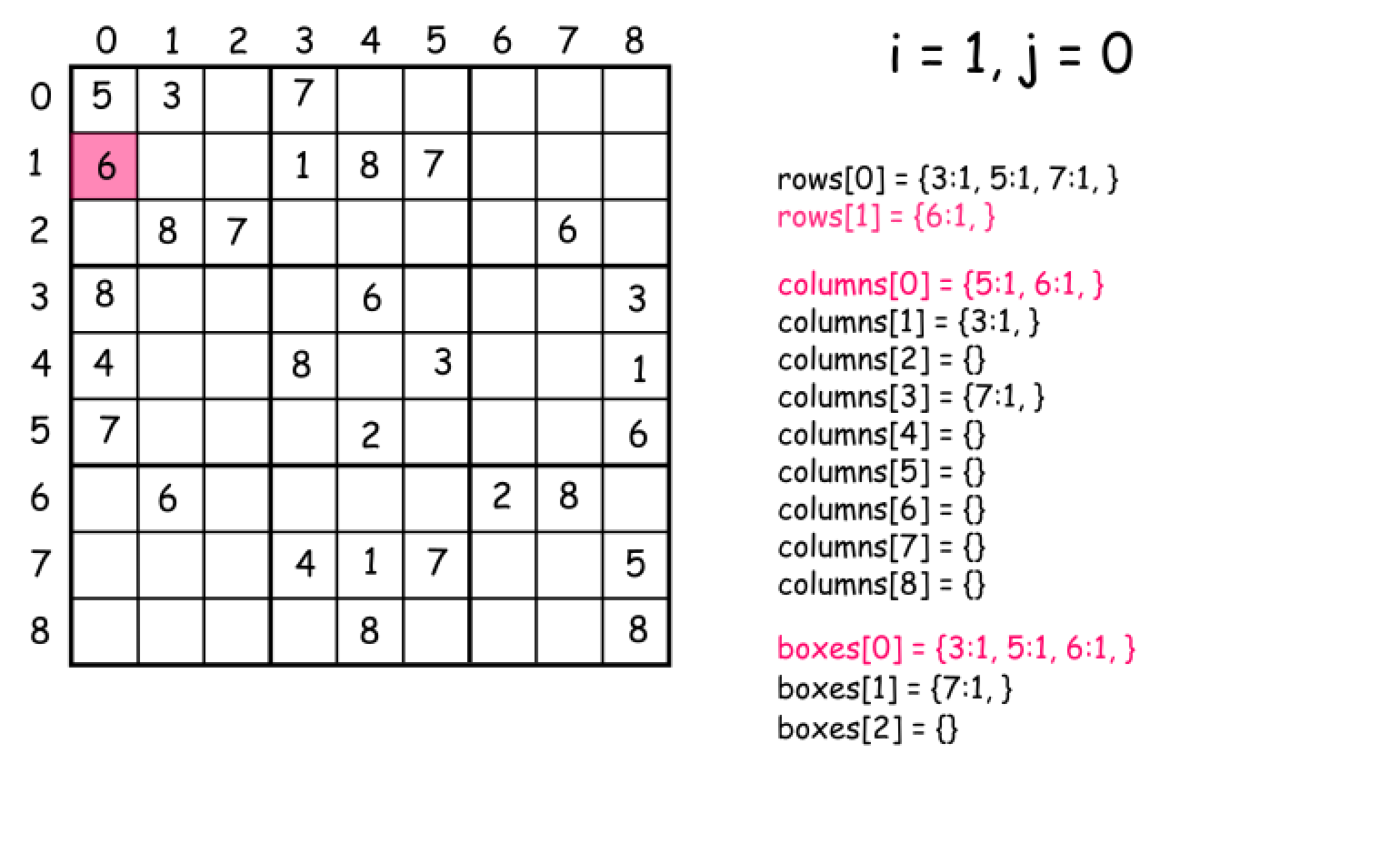
36. 有效的数独
class Solution {
boolean checkRow(char[][] board){
for(int i = 0;i<9;i++){
int[] vis = new int[9];
for(int j = 0;j<9;j++){
if(board[i][j] == '.')continue;
else{
int idx = board[i][j] - '1';
if(vis[idx] == 1){
return false;
}
vis[idx] = 1;
}
}
}
return true;
}
boolean checkCol(char[][] board){
for(int j = 0;j<9;j++){
int[] vis = new int[9];
for(int i = 0;i<9;i++){
if(board[i][j] == '.')continue;
else{
int idx = board[i][j] - '1';
if(vis[idx] == 1){
return false;
}
vis[idx] = 1;
}
}
}
return true;
}
boolean checkBox(char[][] board){
for(int k = 0;k<3;k++){
for(int m = 0;m<3;m++){
int[] vis = new int[9];
for(int i = k*3;i<k*3+3;i++){
for(int j = m*3;j<m*3+3;j++){
if(board[i][j] == '.')continue;
else{
int idx = board[i][j] - '1';
if(vis[idx] == 1){
return false;
}
vis[idx] = 1;
}
}
}
}
}
return true;
}
public boolean isValidSudoku(char[][] board) {
return checkRow(board) & checkCol(board) & checkBox(board);
}
如何映射二维区域 / k 进制映射
i->i / 3j->j / 3
如何组合?
-
idx = (i/3)*3 + j/3; -
这其实是一个三进制
00 01 02 10 11 12 20 21 22
38. Count and Say
class Solution {
int[][] buf;
public String countAndSay(int n) {
buf = new int[2][10000];
int j = 0,count = 0,curi = 1;
buf[1][0] = 1;
for(int i = 2;i<=n;i++){
int[] pre = buf[(i-1) % 2];
int[] cur = buf[(i) % 2];
j = 0;count = 1;curi = 0;
while(pre[j]!=0){
while(pre[j] == pre[j+1]){
j++;
count++;
}
cur[curi++] = count;
cur[curi++] = pre[j];
count = 1;
// 一定不要忘了跳出连续区间
j++;
}
}
StringBuilder s = new StringBuilder();
for(int i = 0;i<curi;i++){
s.append(buf[n%2][i]);
}
return s.toString();
}
}
⭐696. 计数二进制子串
字符串连续字符的统计方法
动态规划的思想
🤔如果是三进制呢?
🤔如果是重复子串不重复记录呢?
🌹Bonus
Rank of Tetris
并查集缩点
并查集的优化
注意:路径压缩 return par[x] = find(par[x]);以及 秩合并,是两种互不关联的优化方法
思路
拓扑排序可能根本因为自环而无法进行下去

环/ 自环的判断
count++;
return count == n;
啊啊!离群点就是初始化时加入队列的点啊,所以,q.size()>0就可以一并包括非联通子图的情况了!!!!😂

// Union + Topo
#include<stdio.h>
#include<string.h>
#include<vector>
#include<queue>
using namespace std;
const int N = 10010;
const int ddd = 0;
//const int ddd = 1;
int in[N];
vector<int> e[N];
int par[N];
int r[N];
int n,m;
int a[N],c[N];
char b[N];
int ns[N];
// union set
int find(int x){
return par[x] == x ? x : par[x] = find(par[x]);
}
void u(int a,int b){
int f1 = find(a);
int f2 = find(b);
if(f1 != f2){
if(r[f1] >=r[f2]){
par[f2] = f1;
ns[f1] += ns[f2];
if(r[f1] == r[f2]) r[f1] ++;
}else if(r[f1] < r[f2]){
par[f1] = f2;
ns[f2] += ns[f1];
}
}
}
void iset(){
for(int i = 0;i<N;i++){
ns[i] = 1;
r[i] = 1;
par[i] = i;
}
}
void show(){
for(int i = 0;i<n;i++){
printf("%d par[%d] = %d ns[%d] = %d in[%d] = %d\n",i,i,par[i],i,ns[i],i,in[i]);
}
}
int main(){
while(scanf("%d %d",&n,&m)!=EOF){
// init
for(int i = 0;i<n;i++){
vector<int>().swap(e[i]);
}
memset(in,0,sizeof(in));
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
iset();
bool conf = false,unc = false;
// read
for(int i = 0;i<m;i++){
int l,r;char op;
scanf("%d %c %d",&l,&op,&r);
if(op == '='){
u(l,r);
b[i] = '=';
}else{
a[i] = l;
b[i] = op;
c[i] = r;
}
}
// post pre-process
for(int i = 0;i<m;i++){
// find the representative
int from = find(a[i]);
int to = find(c[i]);
if(b[i] == '=')continue;
else{
if(from == to){
conf = true;
break;
}
if(b[i] == '>')e[from].push_back(to),in[to]++;
else e[to].push_back(from),in[from]++;
}
if(ddd)printf("from = %d to = %d\n",from,to);
}
queue<int > q;
// init
int count = 0;
for(int i = 0;i<n;i++)
// ignore the points that's shrunk under certain parent point
if(find(i) == i && in[find(i)] == 0){
q.push(i);
count+=ns[i];
}
if(ddd)show();
//self loop(no entry)
if(q.empty() || conf){
printf("CONFLICT\n");
continue;
}
if(ddd)printf("#q = %d\n",q.size());
// Topo Sort
while(!q.empty()){
// uncertain relation
if(q.size() > 1){
unc = true;
// However, because is prior, we cannot break until being sure that there is no conflict
// break;
}
int f = q.front();q.pop();
if(ddd)printf("\t->%d\n",f);
for(int i = 0;i<e[f].size();i++){
// for every outedge
int to = e[f][i];
if(--in[to] == 0) q.push(to),count += ns[to];
}
if(ddd)printf("\tcount = %d\n",count);
}
// topo done
// conf : loop
if(count < n)printf("CONFLICT\n");
// uncertain : multiple same layer / uncoverd vertex
else if(unc)printf("UNCERTAIN\n");
else printf("OK\n");
}
return 0;
}
😅
带权并查集
本文来自博客园,作者:ZXYFrank,转载请注明原文链接:https://www.cnblogs.com/zxyfrank/p/13938843.html