Tarjan 总结及各类题型拓展(缩点篇)
【Tarjan算法的作用】:
- 求强连通分量;
- 缩点(将一个环缩成一个点);
- 割点(这里不谈)……
【Tarjan算法的过程】:
- 初始化数组:dfn[u](时间戳:该节点是第几个被首次访问到的),low[u](low[u]表示u或u的子树所能回溯到的栈中的最早的节点的dfn值)
- 堆栈:将u压入栈顶
- 更新low[u]
- 对于边(u,v),如果v不在栈中,即v是第一次被访问,满足dfn[v]==0;则继续向下找,然后low[u]=min(low[u],low[v]);如果v在栈中,即v已被访问,满足dfn[v]!=0;如果v未被染色,代表v在栈中(dfn[v]!=0表示v进过栈,在栈中的点染色后被弹出,未被染色即未被弹出还在栈中),则low[u]=min(low[u],dfn[v])
5.如果完成上述操作后 low[u]==dfn[u],则将u和在u之后入栈的所有节点弹出,被弹出的所有结点构成一个强连通分量
6.继续搜索(有向图不一定连通),直到所有点都被遍历
【图解】:
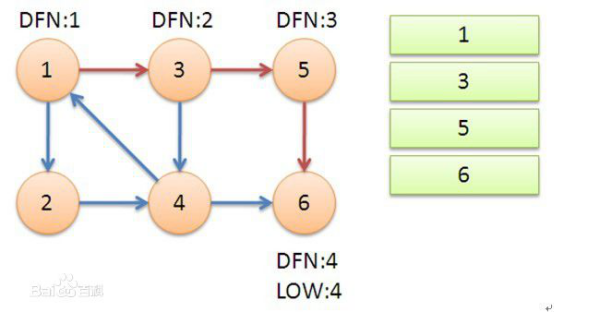
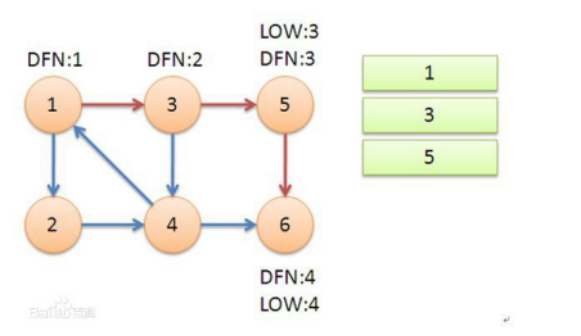
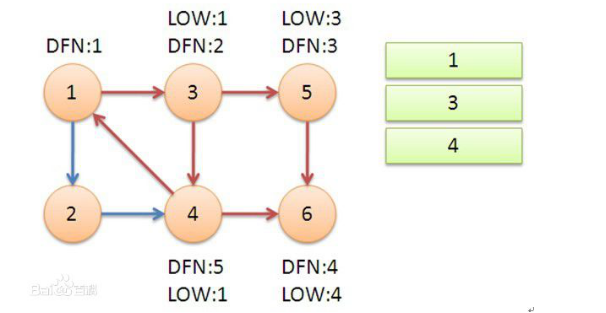
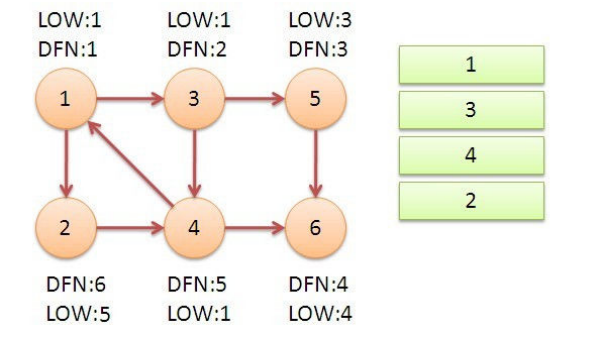
【代码实现】(部分):
struct node{
int ver,next;
}r[]; //邻接表
inline void tarjan(int u){
dfn[u]=++num; //num计数
low[u]=num;
sta[++top]=u; //手写栈,入栈
for(int i=h[u];i;i=r[i].next){
int v=r[i].ver;
if(!dfn[v]){
tarjan(v); //向下找,dfs的思想
low[u]=min(low[u],low[v]);
}
else
if(!c[v]) //如果结点v还在栈中,则v不属于任何强连通分量
low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]){
c[u]=++col; //染色
while(sta[top]!=u){
c[sta[top]]=col;
--top;
}
--top; //将u弹出(退栈)
}
}
【时间复杂度】:O(n+m)
【基础题型】:
1.https://www.luogu.com.cn/problem/P2863
【题目大意】:
有一个 n 个点,m 条边的有向图,请求出这个图点数大于 1 的强联通分量个数。
【题目分析】:
裸题,跳过,直接上代码
注意:求点数大于 1 的强联通分量个数
【代码】:
#include<bits/stdc++.h>
using namespace std;
int n,m,cnt,tot,num,top,ans;
int dfn[10005],low[10005],sta[10005],take[10005],head[10005],color[10005];
struct node{
int ver,next;
}r[200005];
inline void add(int x,int y){
r[++cnt].ver=y;
r[cnt].next=head[x];
head[x]=cnt;
}
inline void tarjan(int x){
dfn[x]=++tot;
low[x]=tot;
sta[++top]=x;
for(int i=head[x];i;i=r[i].next){
int y=r[i].ver;
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
}
else if(!color[y]) low[x]=min(low[x],dfn[y]);
}
if(low[x]==dfn[x]){
color[x]=++num;
while(sta[top]!=x){
color[sta[top]]=num;
--top;
}
--top;
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i);
for(int i=1;i<=n;i++)
take[color[i]]++;
for(int i=1;i<=num;i++)
if(take[i]>1)
ans++;
printf("%d",ans);
return 0;
}
2.https://www.luogu.com.cn/problem/P2002
消息扩散
【题目大意】:
有n个城市,中间有单向道路连接,消息会沿着道路扩散,现在给出n个城市及其之间的道路,问至少需要在几个城市发布消息才能让这所有n个城市都得到消息。
【题目分析】:
当1->2,2->3,3->1时,三点构成一个环,这时无论在哪个城市发布消息,1,2,3三个城市都能得到消息,此时该环等效于一个点,用Tarjan算法缩点,得到有向无环图(可能不止一个)
然后进行拓扑排序(更像一种思想,不会去看一下),在所有入度为0的点(每一个有向无环图的起点)发布消息,然后所有点都可以得到消息
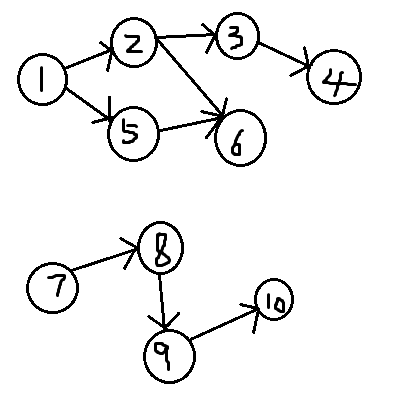
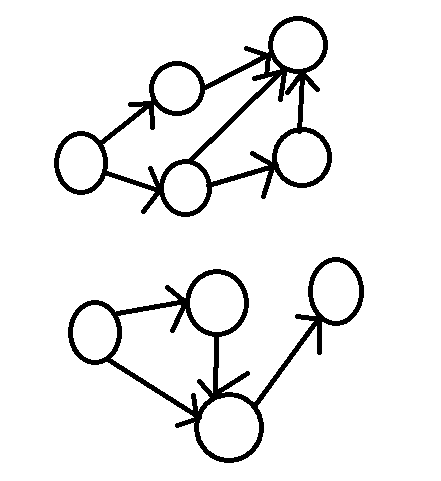
【图解】:
显而易见,只要在所有入度为0的点(有向无环图的起点)(1,7两点)发布消息,所有点就都可以收到消息
【代码】:
#include<bits/stdc++.h>
using namespace std;
int n,m,cr,dsc,col,top,ans;
int c[100005],h[100005],dfn[100005],low[100005],sta[100005],rd[100005]; //rd[i]记录i点的入度
struct node{
int ver,next;
}r[500005];
inline void add(int x,int y){
r[++cr].ver=y;
r[cr].next=h[x];
h[x]=cr;
}
inline void tarjan(int u){
dfn[u]=++dsc;
low[u]=dsc;
sta[++top]=u;
for(int i=h[u];i;i=r[i].next){
int v=r[i].ver;
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else
if(!c[v])
low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]){
c[u]=++col;
while(sta[top]!=u){
c[sta[top]]=col;
top--;
}
top--;
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i);
for(int i=1;i<=n;i++)
for(int j=h[i];j;j=r[j].next){
int l=r[j].ver;
if(c[i]!=c[l]) rd[c[l]]++;
}
for(int i=1;i<=col;i++)
if(rd[i]==0)
ans++;
printf("%d",ans);
return 0;
}
3.https://www.luogu.com.cn/problem/P3387
【模板】缩点
【题目大意】:
给定一个 n 个点 m 条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。允许多次经过一条边或者一个点,但是,重复经过的点,权值只计算一次。求权值和。
【题目分析+图解】:
用一个数组w记录每个点的点权,缩点,再用另一个数组W记录缩点后的每个点的点权(为构成该缩点的所有点的点权之和),得到有向无环图
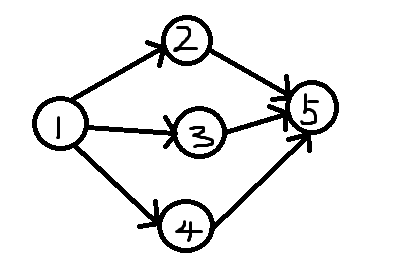
可知:有三条路径:1. 1->2->5
2. 1->3->5
3. 1->4->5
易得:三条路径只需比较后半部分,若要使所选路径的点权值和最大,则2,3,4三点中应选择点权值最大的点
用sum[i]数组进行DP操作,表示从入度为0的点(起点)到i点的路径的最大权值和
注意:需要初始化sum[i]=W[i](只需要初始化入度为0的点,但所有点都初始化也没关系),表示从i点走到i点经过的点的最大权值和(点权)
状态转移方程:sum[l]=max(sum[l],sum[i]+W[l])
【代码】
#include<bits/stdc++.h>
using namespace std;
queue<int> q;
int n,m,cr,cR,col,top,arr,ans;
int w[10005],W[10005],c[10005],h[10005],H[10005],sta[10005],dfn[10005],low[10005],rd[10005],sum[10005]; //小写表示缩点前,大写表示缩点后,c表示染色
struct node{
int ver,next;
}r[100005],R[100005];
inline void add(int x,int y){
r[++cr].ver=y;
r[cr].next=h[x];
h[x]=cr;
}
inline void Add(int x,int y){
R[++cR].ver=y;
R[cR].next=H[x];
H[x]=cR;
}
inline void tarjan(int u){
dfn[u]=++arr;
low[u]=arr;
sta[++top]=u;
for(int i=h[u];i;i=r[i].next){
int v=r[i].ver;
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else
if(!c[v])
low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]){
c[u]=++col;
W[col]+=w[u]; //计算缩点后的点的权值
while(sta[top]!=u){
W[col]+=w[sta[top]];
c[sta[top]]=col;
--top;
}
--top;
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&w[i]);
for(int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i);
for(int i=1;i<=n;i++)
for(int j=h[i];j;j=r[j].next){
int l=r[j].ver;
if(c[i]!=c[l]){
Add(c[i],c[l]);
rd[c[l]]++; //统计入度
}
}
for(int i=1;i<=col;i++) //初始化
sum[i]=W[i];
for(int i=1;i<=col;i++)
if(rd[i]==0)
q.push(i); //入队,进行拓扑排序(bfs),队列里存放入度为0的点
while(q.size()){
int i=q.front();
q.pop();
if(rd[i]==0)
for(int j=H[i];j;j=R[j].next){
int l=R[j].ver;
rd[l]--;
if(rd[l]==0)
q.push(l); //如果入度为0,入队,入队后不会再次入队,无需判断
sum[l]=max(sum[l],sum[i]+W[l]);
}
}
for(int i=1;i<=col;i++)
ans=max(ans,sum[i]); //拓扑排序(搜索)完后再更新ans,否则答案可能会出错
printf("%d",ans);
return 0;
}
【拓展题型】:
4.https://www.luogu.com.cn/problem/P2341
[USACO03FALL][HAOI2006]受欢迎的牛 G
【题目分析】:
易得:存在于同一个强联通分量里的所有牛一定互相受欢迎
那么,找出入度为0的缩点后的点(反向建边),这样可以保证所有的奶牛都喜欢它,但是它不喜欢任何人,所以说不存在其他奶牛明星
特殊情况:如果有两个入度为0的缩点,则不存在奶牛明星,因为这样无法满足所有的牛喜欢他
【代码】:
#include<bits/stdc++.h>
using namespace std;
int n,m,cnt,tot,dsc,col,top,ans;
int c[10005],h[10005],dfn[10005],low[10005],rd[10005],sta[10005],num[10005];
struct node{
int ver,next;
}r[200005];
inline void add(int x,int y){
r[++tot].ver=y;
r[tot].next=h[x];
h[x]=tot;
}
inline void tarjan(int u){
dfn[u]=++dsc;
low[u]=dsc;
sta[++top]=u;
for(int i=h[u];i;i=r[i].next){
int v=r[i].ver;
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else
if(!c[v])
low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]){
c[u]=++col;
num[col]++;
while(sta[top]!=u){
num[col]++;
c[sta[top]]=col;
top--;
}
top--;
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
add(y,x); //反向建边
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i);
for(int i=1;i<=n;i++)
for(int j=h[i];j;j=r[j].next){
int l=r[j].ver;
if(c[i]!=c[l])
rd[c[l]]++;
}
dsc=0;
for(int i=1;i<=col;i++)
if(rd[i]==0){
ans=num[i];
dsc++; //统计入度为0的点的个数
}
if(dsc>1) ans=0; //如果存在两个及两个以上的入度为0的点,则不存在明星奶牛
printf("%d",ans);
return 0;
}
5.https://www.luogu.com.cn/problem/P2746
[USACO5.3]校园网Network of Schools
【题目分析+图解】:
先给你一条链,如何使点上任意一点都可以到达其他所有点
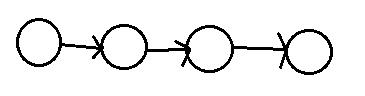
分析一下就很容易想到,只需要加一条边,使该链构成一个环

接下来类比,将树转化为几条链,链数为出度为0的结点(在下面的情况下可理解为树的叶子节点)的个数
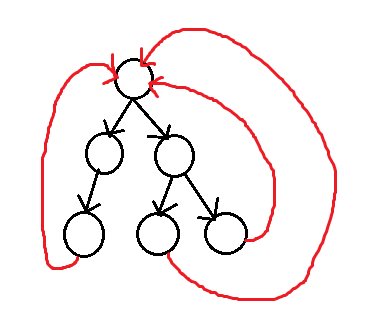
但存在另一种情况
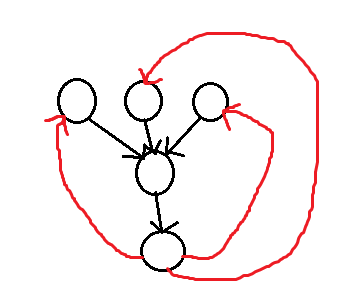
此时链数为入度为0的点的数量
所以需要添加的边的数量为 max(入度为0的点的数量,出度为0的点的数量)
特殊情况见代码
【代码】:
#include<bits/stdc++.h>
using namespace std;
int n,cr,cR,dsc,col,top,lck,ans;
bool V[1000];
int c[1000],h[1000],H[1000],dfn[1000],low[1000],sta[1000],rd[1000],cd[1000]; //cd[]表示出度
struct node{
int ver,next;
}r[100000],R[100000];
inline void add(int x,int y){
r[++cr].ver=y;
r[cr].next=h[x];
h[x]=cr;
}
inline void Add(int x,int y){
R[++cR].ver=y;
R[cR].next=H[x];
H[x]=cR;
}
inline void tarjan(int u){
dfn[u]=++dsc;
low[u]=dsc;
sta[++top]=u;
for(int i=h[u];i;i=r[i].next){
int v=r[i].ver;
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else
if(!c[v])
low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]){
c[u]=++col;
while(sta[top]!=u){
c[sta[top]]=col;
top--;
}
top--;
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int x;
scanf("%d",&x);
while(x!=0){
add(i,x);
scanf("%d",&x);
}
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i);
for(int i=1;i<=n;i++){
memset(V,0,sizeof(V));
for(int j=h[i];j;j=r[j].next){
int l=r[j].ver;
if(V[c[l]]) continue;
if(c[i]!=c[l]){
Add(c[i],c[l]);
V[c[l]]=1;
rd[c[l]]++;
cd[c[i]]++; //同时记录出度和入度
}
}
}
for(int i=1;i<=col;i++){
if(rd[i]==0)
lck++;
if(cd[i]==0)
ans++;
}
if(col==1) //特殊情况:如果整个图缩为一个点,则不需要加边
printf("%d\n0",lck);
else printf("%d\n%d",lck,max(lck,ans));
return 0;
}
6.https://www.luogu.com.cn/problem/P3627
[APIO2009]抢掠计划
【题目分析】:
本题跟【基础题型】3 类似,但如果采用同样的解题方法会超时,那么我们需要一些特殊操作
首先我们需要将点权转化为边权
一条边的权值为该边通向的缩点后的点的点权
然后取负,用SPFA算法搜最短路,然后求出的最小值取负,得到最长路的结果,即为答案
【代码】:
#include<bits/stdc++.h>
using namespace std;
int n,m,s,p,cr,cR,col,dsc,top,ans;
bool V[500005],jb[500005],JB[500005]; //jb[i]表示缩点前i点是否为酒吧,JB[i]表示缩点后i点是否为酒吧
int c[500005],w[500005],W[500005],h[500005],H[500005],dfn[500005],low[500005],sta[500005],dis[500005];
struct node{
int ver,edge,next;
}r[500005],R[500005];
queue<int> q;
inline void add(int x,int y){
r[++cr].ver=y;
r[cr].next=h[x];
h[x]=cr;
}
inline void Add(int x,int y,int z){
R[++cR].ver=y;
R[cR].edge=z;
R[cR].next=H[x];
H[x]=cR;
}
inline void tarjan(int u){
dfn[u]=++dsc;
low[u]=dsc;
sta[++top]=u;
for(int i=h[u];i;i=r[i].next){
int v=r[i].ver;
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else
if(!c[v])
low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]){
c[u]=++col;
W[col]+=w[u];
if(jb[u]) JB[col]=1; //如果该强连通分量中有一点为酒吧,则缩点后可以在该点(结束)统计答案
while(sta[top]!=u){
W[col]+=w[sta[top]];
c[sta[top]]=col;
if(jb[sta[top]]) JB[col]=1;
--top;
}
--top;
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;i++)
scanf("%d",&w[i]);
scanf("%d%d",&s,&p);
for(int i=1;i<=p;i++){
int x;
scanf("%d",&x);
jb[x]=1;
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i);
memset(dis,0x7fffffff,sizeof(dis)); //初始化
dis[c[s]]=-W[c[s]]; //初始化,缩点c[s]没有入度,所以dis[c[s]]权值为点c[s]的点权的相反数
for(int i=1;i<=n;i++){
for(int j=h[i];j;j=r[j].next){
int l=r[j].ver;
if(c[i]!=c[l])
Add(c[i],c[l],-W[c[l]]); //取负
}
}
q.push(c[s]);
while(q.size()){
int x=q.front();
q.pop();
V[x]=0;
for(int i=H[x];i;i=R[i].next){
int j=R[i].ver;
int l=R[i].edge;
if(dis[j]>dis[x]+l){
dis[j]=dis[x]+l;
if(!V[j]) q.push(j);
V[j]=1;
}
}
}
for(int i=1;i<=col;i++)
if(JB[i]) //判断是否可以在该点结束(更新答案)
ans=max(ans,-dis[i]);
printf("%d",ans);
return 0;
}
2020-07-25
2020-10-08


