《数字信号处理》课程实验2 – FIR数字滤波器设计

一、FIR数字滤波器设计原理

 本实验采用窗函数法设计FIR数字低通滤波器。我们希望设计的滤波器系统函数如下：
\(H_{d}\left( e^{jw} \right) = \left\{ \begin{array}{l} {e^{- jw\alpha},~~~\left| w \right| \leq w_{c}} \\ {0,~~~{\rm otherwise}} \\ \end{array} \right.\)
 它对应的单位冲激响应是：
\(h_{d}\left( n \right) = {\sin{\frac{ {w_{c} ( {n - \alpha} ) } }{\pi\left( n - \alpha \right)},~~~n \neq \alpha}}\)
\(w_c\)是截止频率。
 对它进行加窗操作后，单位冲激响应变为：
\(h\left( n \right) = h_{d}\left( n \right)w\left( n \right)\)
其中\(w(n)\)是窗函数的单位冲激响应。
 为了满足FIR滤波器的线性相位特性，我们取系统群时延：
\(\alpha = \frac {N-1}{2}\)
其中\(N\)是FIR滤波器的长度。这样，\(h(n)\)可以关于\(n=α\)偶对称。

二、基于FFT的滤波操作原理

 记待滤波信号为\(x(n)\)，其长度也为\(N\)，则滤波结果信号：
\(y(n)=x(n)*h(n)\)
 左右同作\(2N\)点FFT，有：
\({\rm FFT}_{2N} [y(n)]={\rm FFT}_{2N} [x(n)]∙{\rm FFT}_{2N} [h(n)]\)
 作\(2N\)点FFT的原因是，\(y(n)\)的结果长度为\(2N-1\)，故至少应作\(2N-1\)点FFT才能获得完整结果。又我们在实验1实现的基2-FFT要求点数为2的幂次方，故应作\(2N\)点FFT，且实际上\(2N\)应是2的幂次。
 再做反变换后有：
\(y(n)={\rm IFFT}[{\rm FFT}[y(n)]]\)
这样就获得了滤波结果信号的时域表示。

三、FIR数字滤波器的具体实现

 程序首部可以调节\(w_c\)和\(N\)的取值。本报告中固定\(w_c=0.2π\)，\(N=32\)，后续不再说明。
 首先设计滤波器的无限长冲激响应。我们利用\(N\)的三倍来模拟所谓的无限长。

def h_d(w_c):
  alpha = (N - 1) / 2.  # 系统群时延
  vals = []
  for i in range(N * 3):
    vals.append(math.sin(w_c * (i - alpha)) / float(math.pi * (i - alpha)))
  return vals

 接下来，我们用一个窗函数来截断\(h_d (n)\)。窗函数的选取对滤波器的效果有很大影响。本实验主要关注如下三种窗函数：

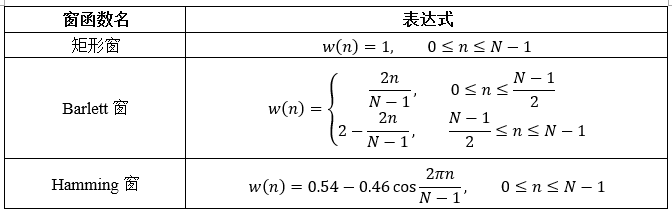
 加窗相关代码如下，以\(N\)为输出长度作对应位相乘即可：

def get_windowed(h_d, w_n):
  cutted = []
  for i in range(N):
    cutted.append(h_d[i] * w_n[i])
  return cutted

以下是相关的时域图像：

 利用实验1写的相关代码，并利用课本193页（《数字信号处理教程》第四版，程佩青）从\(X(k)\)求取\(X(e^{jw})\)的插值公式，可以方便地绘制\(H(e^{jw})\)的幅度函数曲线，举例代码如下：

fft_h_n_rect = fft_dit2(convert_to_complex(add_zero_to_length(h_n_rect, 2 * N)))  # 注意是2N点FFT
plt.title('|H(e^jw)|（矩形窗截断）')
xs, dtft_h_n_rect = interp(fft_h_n_rect, 500)
plt.plot(xs, convert_to_amplitude(dtft_h_n_rect), '-')

插值公式如下：
\(X(e^{{\rm j}w})=\sum_{k=0}^{N-1}{X(k)\Phi(\omega-2\pi k/N)}\)
\(\Phi(\omega)=\frac{1}{N} \frac{\sin(N\omega /2)}{\sin(\omega/2)}e^{-{\rm j}(N-1)\omega/2}\)
绘制结果如下：

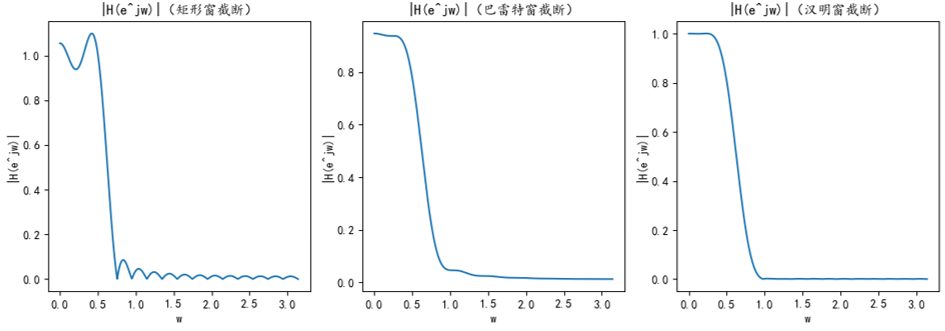
 从这三张幅度频谱图中已经可以清楚地看到不同的窗函数对滤波器的影响：

• 矩形窗的旁瓣抑制性能差，旁瓣峰值大，在阻带仍有一定幅度值；巴特雷特窗旁瓣抑制性能稍好；汉明窗旁瓣抑制能力最强，在阻带基本没有幅度值。
• 矩形窗的主瓣窄；巴特雷特窗的主瓣宽度与汉明窗基本一致。
• 主瓣的宽度影响频率的分辨率，旁瓣的强度影响干扰程度。在实际工程中，应在两者之间进行权衡，选择合适的窗函数。

四、使用FIR数字滤波器进行低通滤波

 本节，我们利用上一节得到的汉明窗截断的FIR滤波器进行低通滤波，使用被噪声污染的正弦函数作为待滤波信号：
\(x\left( n \right) = {\sin n} + {\rm uniform\_ random}\left( - 0.3,~0.3 \right)\)

def get_sin(dot_len):
  xs = np.linspace(-math.pi, math.pi, dot_len)
  ys = [math.sin(x) + random.uniform(-0.3, 0.3) for x in xs]
  return ys

 在\([-π,π]\)上采样的\(N\)点\(x(n)\)的时域图像和\(2N\)点幅度频谱图如下：

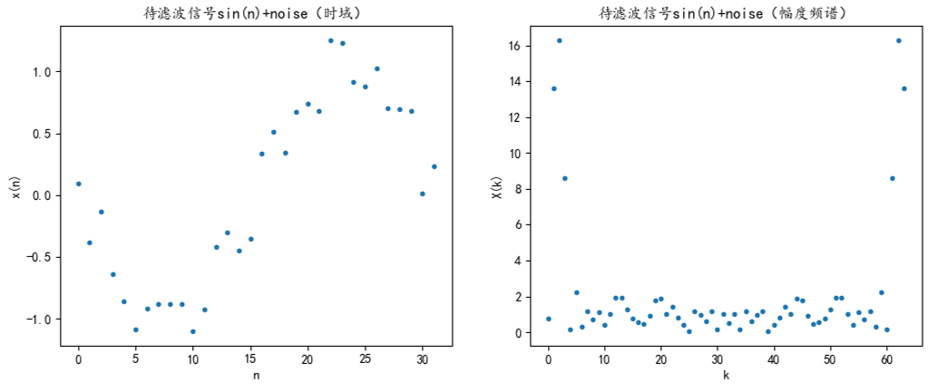
可以看到高频分量具有较大的强度。
 按照第二节提到的公式，在频率域进行滤波，即对应位相乘：

fft_y_n_Hamming = []
for i in range(2 * N):
  fft_y_n_Hamming.append(fft_h_n_Hamming[i] * fft_sin_to_filter[i])  # 计算频域输出

然后把结果作反变换，获得\(2N\)点时域序列，截去最后一个值，即为卷积的时域结果。

y_n_Hamming = convert_to_real(ifft(fft_y_n_Hamming))  # IFFT变回时域
y_n_Hamming = y_n_Hamming[0:-1]  # 去掉最后一个，因为卷积结果长度应为2N-1

 绘制相关图像如下：

 可以看到，高频部分被有效抑制了，噪声被有效消除了，正弦信号被较好地还原了。该FIR滤波器设计和应用成功。

附录：完整代码

fft.py请见实验1
https://www.cnblogs.com/zxuuu/p/12425321.html

---

fir.py

# coding: utf-8
# 《数字信号处理》课程实验
# FIR数字滤波器设计
# 09017227 卓旭

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['KaiTi']  # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False
import math
import random

from fft import *

W_C = 0.2 * math.pi
N = 32

'''
  未加窗的无限长h_d(n)
'''


def h_d(w_c):
  alpha = (N - 1) / 2.  # 系统群时延
  vals = []
  for i in range(N * 3):
    vals.append(math.sin(w_c * (i - alpha)) / float(math.pi * (i - alpha)))
  return vals


'''
  矩形窗
'''


def rect_window(one_len):
  res = []
  for i in range(one_len):
    res.append(1.)
  return res


'''
  Hamming窗
'''


def Hamming_window(length):
  res = []
  for i in range(length):
    res.append(0.54 - 0.46 * math.cos(2 * math.pi * i / (length - 1)))
  return res


'''
  Barlett窗
'''


def Barlett_window(length):
  res = []
  for i in range(0, (length - 1) // 2, 1):  # [0, (N-1)/2)
    res.append(2. * i / (length - 1))
  for i in range((length - 1) // 2, N, 1):  # [(N-1)/2, N-1]
    res.append(2. - 2. * i / (length - 1))
  return res


'''
  待滤波的sin(x)
'''


def get_sin(dot_len):
  xs = np.linspace(-math.pi, math.pi, dot_len)
  ys = [math.sin(x) + random.uniform(-0.3, 0.3) for x in xs]
  return ys


'''
  获取加窗结果
'''


def get_windowed(h_d, w_n):
  cutted = []
  for i in range(N):
    cutted.append(h_d[i] * w_n[i])
  return cutted


'''
  把DFT结果X(k)插值到X(e^jw)
'''


def interp(xk, dot_len=500):
  N = len(xk)
  res = []
  eps = 0.000001

  def phi(w):
    w += eps
    exp_part = Complex(math.cos((1 - N) * w / 2.), math.sin((1 - N) * w / 2.))
    factor = Complex(1 / N * math.sin(N * w / 2.) / math.sin(w / 2.), 0)
    return factor * exp_part

  xs = np.linspace(0, math.pi, dot_len)
  for x in xs:
    sum = Complex(0, 0)
    for i in range(N):
      sum = sum + xk[i] * phi(x - 2. * math.pi * i / N)
    res.append(sum)
  return (xs, res)


if __name__ == '__main__':
  # 生成滤波器无限长冲激响应并绘图
  h_d_n = h_d(W_C)
  plt.title('滤波器的无限长冲激响应')
  plt.xlabel('n')
  plt.ylabel('h_d(n)')
  xs = range(0, N * 3, 1)
  plt.plot(xs, h_d_n, '.')
  plt.show()
  # 生成三种窗
  R_N = rect_window(N)
  Barlett_N = Barlett_window(N)
  Hamming_N = Hamming_window(N)
  # 绘制三种加窗结果（时域）
  h_n_rect = get_windowed(h_d_n, R_N)
  h_n_Barlett = get_windowed(h_d_n, Barlett_N)
  h_n_Hamming = get_windowed(h_d_n, Hamming_N)
  plt.subplot(131)
  plt.xlabel('n')
  plt.ylabel('h(n)')
  plt.title('h(n) （矩形窗截断）')
  xs = range(0, N)
  plt.plot(xs, h_n_rect, '.')
  plt.subplot(132)
  plt.xlabel('n')
  plt.ylabel('h(n)')
  plt.title('h(n) （巴雷特窗截断）')
  plt.plot(xs, h_n_Barlett, '.')
  plt.subplot(133)
  plt.xlabel('n')
  plt.ylabel('h(n)')
  plt.title('h(n) （汉明窗截断）')
  plt.plot(xs, h_n_Hamming, '.')
  plt.show()
  # 将三种加窗转到频域，并绘制其幅度频谱
  fft_h_n_rect = fft_dit2(convert_to_complex(add_zero_to_length(h_n_rect, 2 * N)))  # 注意是2N点FFT
  fft_h_n_Barlett = fft_dit2(convert_to_complex(add_zero_to_length(h_n_Barlett, 2 * N)))
  fft_h_n_Hamming = fft_dit2(convert_to_complex(add_zero_to_length(h_n_Hamming, 2 * N)))
  plt.subplot(131)
  plt.xlabel('w')
  plt.ylabel('|H(e^jw)|')
  plt.title('|H(e^jw)|（矩形窗截断）')
  xs, dtft_h_n_rect = interp(fft_h_n_rect, 500)
  plt.plot(xs, convert_to_amplitude(dtft_h_n_rect), '-')
  plt.subplot(132)
  plt.xlabel('w')
  plt.ylabel('|H(e^jw)|')
  plt.title('|H(e^jw)|（巴雷特窗截断）')
  xs, dtft_h_n_Barlett = interp(fft_h_n_Barlett, 500)
  plt.plot(xs, convert_to_amplitude(dtft_h_n_Barlett), '-')
  plt.subplot(133)
  plt.xlabel('w')
  plt.ylabel('|H(e^jw)|')
  plt.title('|H(e^jw)|（汉明窗截断）')
  xs, dtft_h_n_Hamming = interp(fft_h_n_Hamming, 500)
  plt.plot(xs, convert_to_amplitude(dtft_h_n_Hamming), '-')
  plt.show()
  # 生成噪声干扰后的sin信号待滤波
  sin_to_filter = get_sin(N)  # 获取N点待滤波信号
  plt.subplot(121)
  plt.xlabel('n')
  plt.ylabel('x(n)')
  plt.title('待滤波信号sin(n)+noise（时域）')
  plt.plot(range(0, N), sin_to_filter, '.')
  # 待滤波信号也做2N点FFT
  fft_sin_to_filter = fft_dit2(convert_to_complex(add_zero_to_length(sin_to_filter, 2 * N)))
  plt.subplot(122)
  plt.xlabel('k')
  plt.ylabel('X(k)')
  plt.title('待滤波信号sin(n)+noise（幅度频谱）')
  plt.plot(range(0, 2 * N), convert_to_amplitude(fft_sin_to_filter), '.')
  plt.show()
  # 使用汉明窗截断的滤波器进行低通滤波
  fft_y_n_Hamming = []
  for i in range(2 * N):
    fft_y_n_Hamming.append(fft_h_n_Hamming[i] * fft_sin_to_filter[i])  # 计算频域输出
  plt.subplot(122)
  plt.xlabel('k')
  plt.ylabel('Y(k)')
  plt.title('滤波结果（幅度频谱）')
  plt.plot(range(0, 2 * N), convert_to_amplitude(fft_y_n_Hamming), '.')
  y_n_Hamming = convert_to_real(ifft(fft_y_n_Hamming))  # IFFT变回时域
  y_n_Hamming = y_n_Hamming[0:-1]  # 去掉最后一个，因为卷积结果长度应为2N-1
  plt.subplot(121)
  plt.xlabel('n')
  plt.ylabel('y(n)')
  plt.title('滤波结果（时域）')
  plt.plot(range(0, 2 * N - 1, 1), y_n_Hamming, '.')
  plt.show()