傅里叶变换在图像处理中的应用
任何周期函数都可以表示为不同频率的正弦和/或余弦之和的形式，每个正弦项和/或余弦项乘以不同的系数（现在称该和为傅里叶级数）。无论函数多么复杂，只要它是周期的，并且满足某些适度的数学条
件，都可以用这样的和来表示。即一个复杂的函数可以表示为简单的正弦和余弦之和。甚至非周期函数（单该曲线下的面积是有限的）也可以用正弦和/或许·余弦乘以加权函数的积分来表示。在这种情况下的公式
就是傅里叶变换。傅里叶变换是一种分析信号的方法，它可分析信号的成分，也可用这些成分合成信号。许多波形可作为信号的成分，比如正弦波、方波、锯齿波等，傅里叶变换用正弦波作为信号的成分。
傅里叶变换在很多方面均有应用，这里主要介绍一下傅里叶变换和在图像增强中的应用。
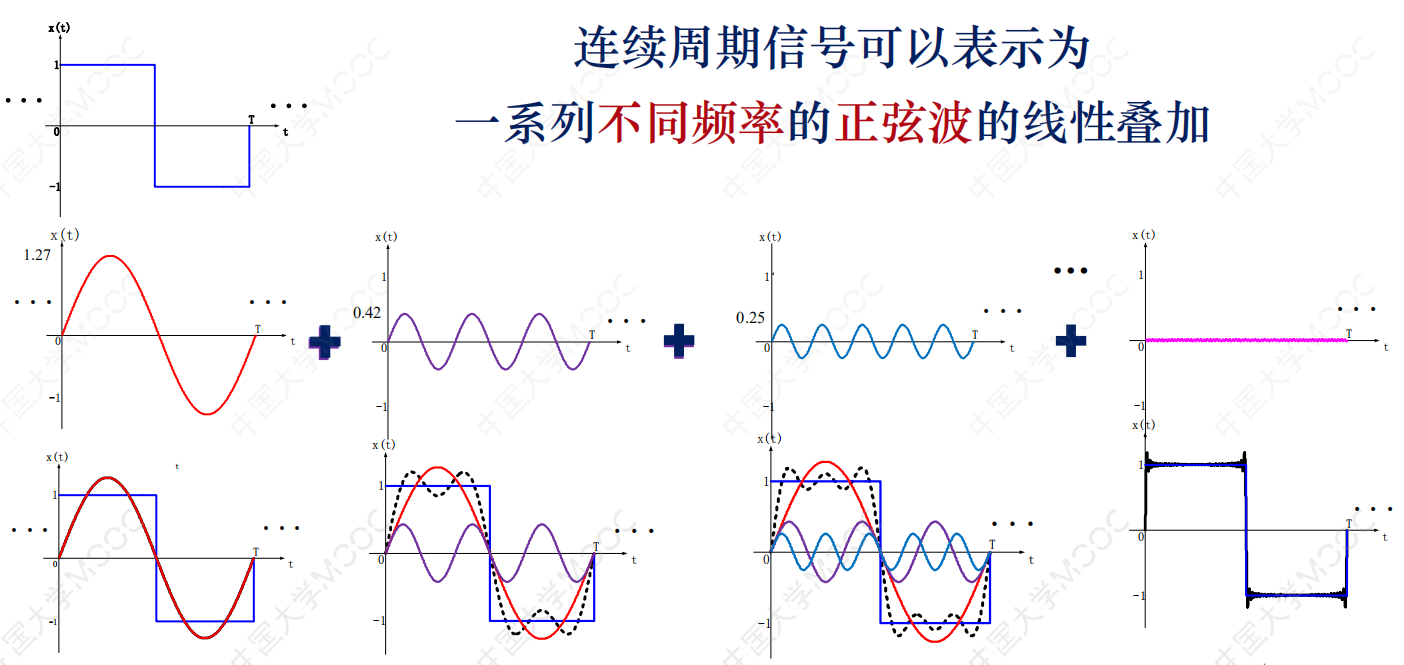
时域与频域
（1）频域（frequency domain）是指在对函数或信号进行分析时，分析其和频率有关部份，而不是和时间有关的部分，和时域一词相对。
（2）时域是描述数学函数或物理信号对时间的关系。例如一个信号的时域波形可以表达信号随着时间的变化。若考虑离散时间，时域中的函数或信号，在各个离散时间点的数值均为已知。
若考虑连续时间，则函数或信号在任意时间的数值均为已知。在研究时域的信号时，常会用示波器将信号转换为其时域的波形。
（3）两者相互间的变换
时域（信号对时间的函数）和频域（信号对频率的函数）的变换在数学上是通过积分变换实现。对周期信号可以直接使用傅立叶变换，对非周期信号则要进行周期扩展，使用拉普拉斯变换。
周期信号的傅里叶级数表示
连续时间非周期信号的傅里叶变换
一维离散信号傅里叶变换及傅里叶反变换
将一维离散信号傅里叶变换推广到二维傅里叶变换
将傅里叶变换表示成复数形式
我们将一幅图像进行傅里叶变换后，结果如下：
快速傅里叶变换（FFT）
计算离散傅里叶变换的一种快速算法，简称FFT。函数或信号可以透过一对数学的运算子在时域及频域之间转换。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散
傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。
人们想让计算机能处理信号，但由于信号都是连续的、无限的，计算机不能处理，于是就有了傅里叶级数、傅里叶变换，将信号由时域变到频域，把一个信号变为有很多个不同频率不同幅度的正弦信号组
成，这样计算机就能处理了，但又由于傅里叶变换中要用到卷积计算，计算量很大，计算机也算不过来，于是就有了快速傅里叶变换，大大降低了运算量，使得让计算机处理信号成为可能。快速傅里叶变换是傅
里叶变换的快速算法而已，主要是能减少运算量和存储开销，对于硬件实现特别有利。
图像中傅里叶变换的意义
图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。如：大面积的沙漠在图像中是一片灰度变化缓慢的区域，对应的频率值很低；而对于地表属性变换剧烈的边缘区域在图像是
一片灰度变化剧烈的区域，对应的频率值较高。傅立叶变换在实际中有非常明显的物理意义，设 ff 是一个能量有限的模拟信号，则其傅立叶变换就表示 ff 的谱。当图像使用空间域等手段并不能取得良好的图像增
强效果的时候，这时候可以考虑使用傅里叶变换的方法，即将图像先进行傅里叶变换转换为频域系统，然后经过处理（一般是设计一个低通或者高通滤波器，这里就涉及到频域滤波的种类了，这里先不赘述），
再转换为空间域图像。会取得良好的效果。从纯粹的数学意义上看，傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看，傅立叶变换是将图像从空间域转换到频率域，其逆变换是将图像从
频率域转换到空间域。换句话说，傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数，傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。
实际上对图像进行二维傅立叶变换得到频谱图，就是图像梯度的分布图，当然频谱图上的各点与图像上各点并不存在一一对应的关系，即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一
的亮点，实际上图像上某一点与邻域点差异的强弱，即梯度的大小，也即该点的频率的大小（可以这么理解，图像中的低频部分指低梯度的点，高频部分相反）。一般来讲，梯度大则该点的亮度强，否则该点亮
度弱。我们首先就可以看出，图像的能量分布，如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小），反之，如果频谱图中亮的点数多，那么实际图像一定是
尖锐的，边界分明且边界两边像素差异较大的。对频谱移频到原点以后，可以看出图像的频率分布是以原点为圆心，对称分布的。
关于图像梯度，可以看这篇博客【图像梯度的基本原理】
