P5659 [CSP-S2019] 树上的数 题解
P5659 [CSP-S2019] 树上的数 题解
前言
好不容易今天晚上有时间，自己再造一遍，加深一下印象，再总结一下这类问题的思路
思路：
先来分析一下题目类型，既有节点编号，节点编号上有权值编号，可以实现权值更换，但规定次数，最终按照权值大小输出编号 （其实就是题目大意） 这种操作类就很烦，我看到不是数据结构就是DP，可它出在树上，这就没有任何办法，只能靠自己寻找题目中的性质。这也非常考察一个OI的做题能力，在没有任何算法的情况下去面对联赛的T3，可还行？
题目最终的要求是让数字从小到大排列得到的序列，因此我们整个题目应该尽可能多注意如何处理数字，而不是关注序号怎么排最小。
10pts
数据很小，不会就全部枚举，把所有的交换次数都模拟一遍，最后挨个比较，这样够暴力了，然而这里有考察了全排列，正常人很快就会写出来，只有我这愚人半天写不出来
这里我们用 pair 记录路径，暴力的去交换路径，得到全排列，处理时这里还学到了权值排序的一种算是思想吧，整个题都会贯穿
for (int i=1;i<=n;i++) mir[a[i]]=i;
我们将每一个权值都用 \(mir\) 存储数字实际对应的编号，我们的目的是让数字从小到大排序，所以每得到一个序列，完成 \(mir\) 的赋值，只需要和当前的答案按数字从小到大比较就好了，其实是个人都会
/*
单纯练码，
10pts 大约15min
*/
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;
const int A = 1e7+10;
const int B = 1e6+10;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
inline int read() {
char c = getchar();
int x = 0, f = 1;
for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
return x * f;
}
pair<int,int>pp[B];
int a[B],T,n;
int mir[B],ans[B],vis[B];
void dfs(int dep)
{
if (dep==n)
{
for (int i=1;i<=n;i++) mir[a[i]]=i;//里面存的是数字
for (int i=1;i<=n;i++)
{
if (mir[i]<ans[i])
{
for (int j=1;j<=n;j++)
{
ans[j]=mir[j];
// printf("%d ",ans[j]);
}
// puts("");
break;
}
else if (mir[i]>ans[i]) break;
}
return;
}
for (int i=1;i<n;i++)
{
if (!vis[i])
{
int x=pp[i].first,y=pp[i].second;
swap(a[x],a[y]); vis[i]=1;
dfs(dep+1);
swap(a[x],a[y]); vis[i]=0;
}
}
}
void work1()
{
for (int i=1;i<=n;i++) printf("%d ",ans[i]);
puts("");
}
int main()
{
T=read();
while (T--)
{
n=read();
memset(vis,0,sizeof(vis));
for (int i=1;i<=n;i++) a[read()]=i,ans[i]=n-i+1;
for (int i=1;i<n;i++) {int u=read(),v=read(); pp[i]=make_pair(u,v);}
if (n<=10) {dfs(1);work1();}
}
}
菊花图
这里先说明一个贪心，这是使全排列\(O(n!)\) 变成 \(O(n^2)\) 的方法
我们期望的，必然是想要小的数字尽量在小的标号前面，看这个例子
数字 \(1\) 现在可以和 \(1\) 和 \(5\) 换，你选谁，肯定是 \(1\) 为什么这样选，仅仅是当前状态下更优吗？
我们在考虑后效性，数字 \(1\) 位置上如果是 \(5\) 即使后是最完美的 \(1,2, 3, 4,\) 的字典序，都不会比数字 \(1\) 位置上是\(1\) 的最劣\(5,4,3,2\) 优，、
因此能和小数换，决不和大数换，换句话讲，小的数字尽量跟小的编号匹配，剩下的无论好不好，都强制匹配上（只会强制一个，因为小数字前面的匹配到的决不是所拥有状态中最劣的）
有了这贪心，我们再来看部分分，
我们的目的是关注数字而不是编号，因为编号我们可以贪心求得，但前提是如何操作数字，我们随便模拟题目交换顺序，
\(1\to 4\) 则 \(Y_7\to Y_1\) 这里指的是，\(Y_7\) 来到了 \(Y_1\) 的位置上，至于 \(Y_1\) 则来到的花心处
\(1\to 5\) 则 \(Y_1\to Y_4\) ，\(Y_4\) 来到花心，
我们来观察 \(Y1\) 从开始到完成第二次操作他做了什么？
从 \(4\to 5\) ，直观的讲 \(Y_1\to\) 原来 \(Y_4\) 的位置，即位置 \(5\) ，并且我们发现 \(Y1\) 不会在移动了，我们不妨记作 \(Y_1\to Y_4\)
那么其他非花心的点是否也是这样的操作呢？
不难发现，是的，并且我们会得到许多类似 \(Y_{...}\to Y_{...}\) 的样子，自己找个小图手摸一下，这个太大了，我不好写出了，总之（比较敷衍，最终构成结束点会在花心结束，并且将所有的 \(\to\) 连接起来，他构成了一个环
我们从花心处将环断开就得到了一个链，我这样做有什么用呢？
但凡是个合理的交换顺序，他从花心处断开一定一条链，绝不会产生环（显而易见
那么答案必定也是一条链，
所以找最小链就好了，怎么做还是全排列枚举吗，不用我们上面的贪心，这样就轻而易举的完成了
所以我们来盘点一下需要处理的东西
-
不能有环，并查集查询搞一搞
-
\(O(n^2)\) 贪心搞一搞
-
如何答案记录？
ans[mir[i]]=j;//编号变成了j代码里呈现了这样的语句，自认为不太好理解，所以来说一下
解释为：数字大小为 \(i\) 对应的编号在操作中被更为了 \(j\)
for (int i=1;i<=n-1;i++) printf("%d ",ans[mir[i]]); for (int i=1;i<=n;i++) if (!vis[i]) printf("%d",i);答案查询时，只要从小到大数字就好了，注意，我们保证了不能有环，那么必然有一个数字是没有转移的，因为我们贪心，必然是数字大小为最大一个没有匹配，这时强制匹配就好了，前面都是最优的，并且又是最后一个，形成的序列不就是最优的吗？真优美！
/*
单纯练码，
10pts 大约15min
35pts 9:00 大约18min 居然这么快，
*/
pair<int,int>pp[B];
int a[B],T,n;
int mir[B],ans[B],vis[B];
int du[B],fa[B];
int find(int x){return (fa[x]==x) ? x : fa[x]=find(fa[x]);}
void work2()
{
for (int i=1;i<=n;i++) fa[i]=i;//重置
for (int i=1;i<=n;i++) mir[a[i]]=i;
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
{
int fx=find(mir[i]), fy=find(j);
if (vis[j] || fx==fy) continue;
ans[mir[i]]=j;//编号变成了j
fa[fy]=fx;
vis[j]=1;
break;
}
int flag=0;
for (int i=1;i<=n-1;i++) printf("%d ",ans[mir[i]]);
for (int i=1;i<=n;i++) if (!vis[i]) printf("%d",i);
puts("");
}
int main()
{
// freopen("tree.in","r",stdin);
// freopen("tree.out","w",stdout);
T=read();
while (T--)
{
int maxx=0;
n=read();
memset(vis,0,sizeof(vis));
memset(du,0,sizeof(du));
for (int i=1;i<=n;i++) a[read()]=i,ans[i]=n-i+1;
for (int i=1;i<n;i++)
{
int u=read(),v=read();
du[u]++,du[v]++;
pp[i]=make_pair(u,v);
maxx=max(du[u],max(du[v],maxx));
}
if (n<=10) {dfs(1);work1();}
else if (maxx==n-1)//菊花图
{
work2();
}
}
}
链壮
首先要想处理链上的东西，就必须知道他们之间的边关系，所以需要建边，得到每个点之间的位置关系
即：
void get_path(int u,int pre)
{
tot[pt[u]=++num]=u;
for (int i=head[u];i;i=e[i].nxt)
{
int v=e[i].v;
if (v==pre) continue;
get_path(v,u);
}
}
再考虑怎么贪心
贪心的思路没变，就是让小的尽量找小的，那么看下面的情景
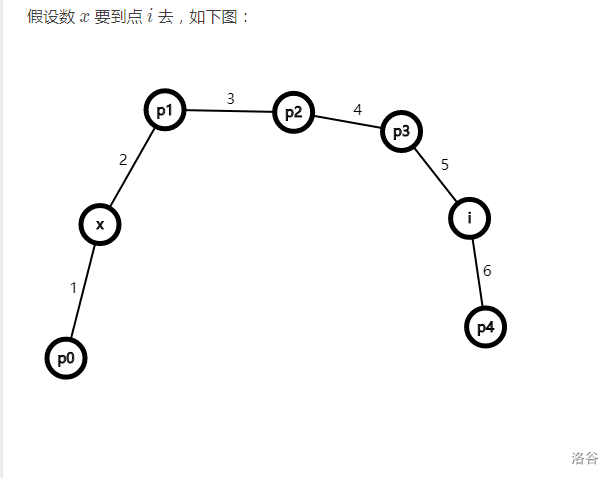
假设此时的 \(x\) 就是最小数字 \(1\) 而 \(i\) 就是我们贪心贪的 \(1\) ，因此我们应该尽可能的让 \(x\) 来到 \(i\) 点，我们观察每个点连接的两条边删除的先后顺序，发现 \(x\to i\) 只有 \(x,i\) 的是先删右边再删左边，路径上的其他点都是先删左边再删右边，这个奇妙的思路我们不妨试一下
用 \(mark\) 标记该点边删除的顺序
-
未标记-0
-
先右后左-2
-
先左后右-1
-
有了这种限制，我们不妨想让数字\(x\) 转移到 \(j\) 点是否可用性，就只需要判断路径上的每一个点的标记是否满足条件，若是右移则为：\(211..(1)2\)，反之：\(122..(2)1\)
只要被标记的在以后的贪心里就不会被更改了，换句话说，为了使当前最小，路径上的都强制跟周围两侧的交换了，
所以我们就做出来了
写几个我出错的地方
void ch_l(int x,int y)
{
if (pt[x]!=1 && pt[x]!=n) mark[pt[x]]=1;
for (int i=pt[x]+1;i<=pt[y]-1;i++) mark[i]=2;
if (pt[y]!=1 && pt[y]!=n) mark[pt[y]]=1;
}
中间循环的时候是 x+1..y-1 这并不是得到的位置
if (pt[x]<=pt[y])//需要右移
{
if (checkl(x,y))//可以右移 也可以认为再次没有被操作过
{
ch_r(x,y);
flag=1;
}
}
if 没有登号，导致已经被强制修改的点没有更新
for (int i=pt[x]+1;i<=pt[y]-1;i++) if (mark[i]==2) return 0;
后面的mark[i] 写成 mark[pt[i]] 大意了！
/*
单纯练码，
10pts 大约15min
35pts 9:00 大约18min 居然这么快，
*/
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;
const int A = 1e7+10;
const int B = 1e6+10;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
inline int read() {
char c = getchar();
int x = 0, f = 1;
for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
return x * f;
}
pair<int,int>pp[B];
int a[B],T,n;
int mir[B],ans[B],vis[B];
void dfs(int dep)
{
if (dep==n)
{
for (int i=1;i<=n;i++) mir[a[i]]=i;//里面存的是数字
for (int i=1;i<=n;i++)
{
if (mir[i]<ans[i])
{
for (int j=1;j<=n;j++)
{
ans[j]=mir[j];
// printf("%d ",ans[j]);
}
// puts("");
break;
}
else if (mir[i]>ans[i]) break;
}
return;
}
for (int i=1;i<n;i++)
{
if (!vis[i])
{
int x=pp[i].first,y=pp[i].second;
swap(a[x],a[y]); vis[i]=1;
dfs(dep+1);
swap(a[x],a[y]); vis[i]=0;
}
}
}
void work1()
{
for (int i=1;i<=n;i++) printf("%d ",ans[i]);
puts("");
}
int du[B],fa[B];
int find(int x){return (fa[x]==x) ? x : fa[x]=find(fa[x]);}
void work2()
{
for (int i=1;i<=n;i++) fa[i]=i;//重置
for (int i=1;i<=n;i++) mir[a[i]]=i;
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
{
int fx=find(mir[i]), fy=find(j);
if (vis[j] || fx==fy) continue;
ans[mir[i]]=j;//编号变成了j
fa[fy]=fx;
vis[j]=1;
break;
}
int flag=0;
for (int i=1;i<=n-1;i++) printf("%d ",ans[mir[i]]);
for (int i=1;i<=n;i++) if (!vis[i]) printf("%d",i);
puts("");
}
struct node{int v,nxt;}e[B];
int head[B],cnt;
void modify(int u,int v)
{
e[++cnt].nxt=head[u];
e[cnt].v=v;
head[u]=cnt;
}
int pt[B],num,mark[B],tot[B];// 0 无标记 1 先左后又， 2先右后左
void get_path(int u,int pre)
{
tot[pt[u]=++num]=u;
for (int i=head[u];i;i=e[i].nxt)
{
int v=e[i].v;
if (v==pre) continue;
get_path(v,u);
}
}
bool checkl(int x,int y)//检查右移满足的条件
{
if (mark[pt[x]]==1) return 0;
for (int i=pt[x]+1;i<=pt[y]-1;i++) if (mark[i]==2) return 0;
if (mark[pt[y]]==1) return 0;
return true;
}
void ch_r(int x,int y)
{
if (pt[x]!=1 && pt[x]!=n) mark[pt[x]]=2;
for (int i=pt[x]+1;i<=pt[y]-1;i++) mark[i]=1;
if (pt[y]!=1 && pt[y]!=n) mark[pt[y]]=2;
}
bool checkr(int x,int y)//检查左移满足的条件
{
if (mark[pt[x]]==2) return 0;
for (int i=pt[x]+1;i<=pt[y]-1;i++) if (mark[i]==1) return 0;
if (mark[pt[y]]==2) return 0;
return true;
}
void ch_l(int x,int y)
{
if (pt[x]!=1 && pt[x]!=n) mark[pt[x]]=1;
for (int i=pt[x]+1;i<=pt[y]-1;i++) mark[i]=2;
if (pt[y]!=1 && pt[y]!=n) mark[pt[y]]=1;
}
void work3()
{
num=0;
for (int i=1;i<=n;i++) if (du[i]==1) {get_path(i,0); break;}//得到具体位置
for (int i=1;i<=n;i++) mir[a[i]]=i,vis[i]=0,mark[i]=0;
for (int i=1;i<=n;i++)
{
for (int j=1;j<=n;j++) if (!vis[j] && pt[mir[i]]!=pt[j])//二者位置不能重合
{
int flag=0;
int x=mir[i],y=j;
if (pt[x]<=pt[y])//需要右移
{
if (checkl(x,y))//可以右移 也可以认为再次没有被操作过
{
ch_r(x,y);
flag=1;
}
}
else
{
if (checkr(y,x))//可以左移
{
ch_l(y,x);
flag=1;
}
}
if (flag)//可以替换
{
ans[i]=j; vis[j]=1;
break;
}
}
}
for (int i=1;i<=n;i++) printf("%d ",ans[i]);
// for (int i=1;i<=n;i++) if (!vis[i]) {printf("%d",i);break;}
puts("");
}
int main()
{
// freopen("tree.in","r",stdin);
// freopen("tree.out","w",stdout);
T=read();
while (T--)
{
int maxx=0;
n=read();
cnt=0;
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
memset(du,0,sizeof(du));
for (int i=1;i<=n;i++) a[read()]=i,ans[i]=n-i+1;
for (int i=1;i<n;i++)
{
int u=read(),v=read();
du[u]++,du[v]++;
pp[i]=make_pair(u,v);
maxx=max(du[u],max(du[v],maxx));
modify(u,v), modify(v,u);
}
if (n<=10) {dfs(1);work1();}
else if (maxx==n-1)//菊花图
{
work2();
}
else if (maxx==2)
{
work3();
}
}
}
