DP斜率优化
斜率优化
hdu3507
要输出N个正数字 ,输出的时候可以连续的输出,每连续输出一串,它的费用是 :这串数字和的平方加上一个常数 。 求费用最小。
网课手推式子
上述式子正确
时间复杂度为 , 直接起飞~
前方高能
我们对上述式子进行定义:
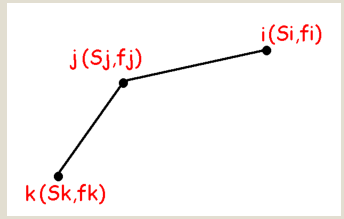
我们定义两个决策点, 并且 , 那么我们要想使 值从 转移的解比从 的更优的条件应该符合什么?
代入式子得:
移项得
最终得
令 ,代换得
故当条件满足上述不等关系时, 比 转移更优,(这里指的是位置更靠后)
我们将 看做一个点的话,那么上述式子则表示的就是斜率公式(纵差比横差),故我们可以画出两点之间的斜率
那么对于我们所求的当前 ,中上述三个决策点的劣优就可以得到了 为:,前提是我们必须知道不等关系右边的大小
现在推到广义上, 变量之间不知道存在的位置大小关系,
那么就存在三种情况
第一种:
优劣程度:
第二种
优劣程度:
第三种
优劣程度:
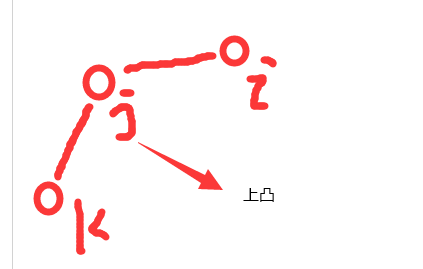
故我们在这三种情况下得出不可能是最优的,那么它就可以不做决策点,即上凸图像不可做决策点
因此我们只需要维护下凸点即可,具体就是用队列进行维护
对于不同的斜率不等式,需要维护的凸点是不同的,小于就是维护下凸,大于维护上凸
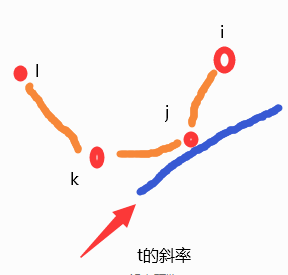
问题是凸包中谁是更优呢?
自然就是斜率不大于当前斜率
边界是
优劣程度:
若大于,则前者优
若小于,则后者优,故 比 更优
二分(在右侧不存在单调性)
实现方式:
找到不大于 的最大位置,如果判断出 比 优,那么往后的 都不会在用到 ,因此可以将 剔除,为什么?因为 存在单调性,往后的值只会用到当前有用的决策点,并且优先选择更优的决策点,那么留着 干什么,所以提出
这个过程可以利用单调队列来维护,保证队列中一直是当前有用决策点的集合
对于当前不合法的就直接出队, 合法但不是已经有比他更优的也弹出队
int getup(int j, int k)
{
return dp[j] + sum[j] * sum[j] - dp[k] - sum[k] *sum[k]
}//推导式中上部分
int getdown(int j, int k)
{
return 2 * (sum[j] - sum[k])
}
int getdp(int i, int j)
{
return dp[j] + (sum[i] - sum[j]) * (sum[i] - sum[j]) + m
}
head = tail = 1;
q[1] = 0;
for (int i = 1; i<= n; i++)
{
while (head < tail && getup(q[head+1], q[head])) <= sum[i] * getdown(q[head+1], q[head]) head++;
//(合法与不合比较)
dp[i] = getdp(i, q[head]);
while (head < tail && getup(i, q[tail]) * getdown(q[tail], q[tail-1])<=getup(q[tail], q[tail] - 1) * getdown(i, q[tail])) tail--;
//队首的下一个比队首更优,那么就将它弹出
//合法中更优解比较,若斜率之比更小1,那么前者小于后者,即 i 优于 tail, 那么tail 在以后的比较将不会被用到,那么弹出
q[++tail] = i;
//将可能是以后的更优解加入队列,为什么是可能?因为它可能也会被下一个所代替,不过还是需要让他入队,
//我们不知道他的作用,即使无用在下一次的决策点判断中也会弹出
}
引进概念
类型 : 优化状态转移
模式:
假定决策点之间的位置关系,
代入推公式
得到斜率公式,跑单调队列
"" 维护下凸 "" 维护上凸
BZOJ3156
推到的话我就省略了,为了简单好推,用
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;
const int A = 1e7+10;
const int B = 1e6+10;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
inline ll read() {
char c = getchar();
ll x = 0, f = 1;
for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
return x * f;
}
ll n,a[B],f[B],head,tail,q[B],ans,t;
double xie(ll k,ll j)
{
return ((2.0*(f[k]-f[j])+k*(k+1)-j*(j+1))/(2*k-2*j));
}
int main()
{
n=read();
for (ll i=1;i<=n;i++) a[i]=read();
for (ll i=1;i<=n/2;i++) t=a[i],a[i]=a[n-i+1],a[n-i+1]=t;
head=tail=1ll;
q[1]=1ll;
f[1]=a[1];
ans=a[1]+1ll*n*(n-1)/2ll;
for (ll i=2;i<=n;i++)
{
while (head<tail && xie(q[head+1],q[head])<i) head++;
f[i]=f[q[head]]+1ll*(i-q[head])*(i-q[head]-1)/2+a[i];
ans=min(ans,f[i]+1ll*(n-i+1)*(n-i)/2);
while (head<tail && xie(q[tail],q[tail-1])>xie(i,q[tail])) tail--;
q[++tail]=i;
}
printf("%lld",ans);
}
总结
斜率优化就是通式
抽象的点 需要单调, 不需要
不等式右边的需要保证单调性,不单调就二分查找维护
本文作者:zxsoul
本文链接:https://www.cnblogs.com/zxsoul/p/14383808.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步