剪枝例题大全+题解
「一本通 1.3 例 1」数的划分
题目描述
将整数 分成 份,且每份不能为空,问有多少种不同的分法。
思路
-
写题解的原因就是本题并不是一个简单的搜索,而是一个可行性剪枝,即“上下界剪枝”
-
将题用数学语言就是 解方程
-
因为答案没要求次序,我们定义为递增(避免重复),那么不难发现 ,这就是下界
-
当求第 数字时,还需要拼购 个数字,注意是个数!那么如果这个数过于大的话,后面一定拼不起来,所以我们可以发现当前数 最多不能超过 即 往后的平均数,就是上界
-
所以每次枚举就可一下缩小范围了,快着不只一点呐

Code
#include <iostream>//可行性剪枝
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
const int manx=1e6+10;
const int mamx = 1e6 + 11;
const ll mod = 2123400401301379571;
const int inf = 0x3f3f3f3f;
inline int read() {
char c = getchar(); int x = 0, f = 1;
for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
return x * f;
}
int n,m,a[manx],ans;
void dfs(int k){
if(n == 0) return;//下一步的操作让n不可能为零,所以n为零就是证明取数过大,需要返回
if(k == m){
if(n >= a[k - 1]) ans++;//第m次填数时如果剩下的数满足下界条件,即a[i-1]<= a[i],那就直接记录答案中
return;
}
for(int i = a[k-1];i <= n/(m - k + 1); i++)// k 的 下界 和 上界
{
a[k] = i;
n -= i;
dfs(k+1);
n += i;
}
}
int main(){
n = read();
m = read();
a[0] = 1;//边界
dfs(1);
cout<<ans<<endl;
return 0;
}
「一本通 1.3 例 5」weight
题面
给定原数列 ,给定每个数的前缀和以及后缀和,并且打乱顺序。
给出一个集合 要求从集合 中找到合适的数,满足给定的所有数例前缀和和后缀和,答案保证最小的
思路
很多人上来没有思路,不知从何搜起
-
简单讲就是找到正确的搜索顺序,往里面放数就好了
他不是有前缀和也有后缀和嘛~,而且还是混着的,
那么你就直接排序,然后安排两个指针 和 的表示左边和右边,
记录每个 的前缀和 和 的后缀和,然后用当前的你所枚举的(题中给出的混杂数列) 相减,即 ,
只要相减的差在给定集合 里,直接搜索下一层,两个指针肯定会跑到一起,最后再判断答案合不合限定范围就可以了
-----------------------------------------------------------------------分割线----------------------------
-
详细的说 就是通过给定的条件,找到约束条件,进而说明我为什么要选择上面的搜索顺序和思路
- 令 满足要求的 (原数列 ,右同),表示位置 的前缀和 ,
- 令 满足要求的 表示位置 的后缀和,
- 令 为答案数列
不难发现
可以将打乱的先排序,最后的数显然就是 和 , 最小的数 要不是最左边,要不是最右边。(剪枝1)
我们从已知条件的数据当中任意取出两个数的时候,只会出现以下两种情况:
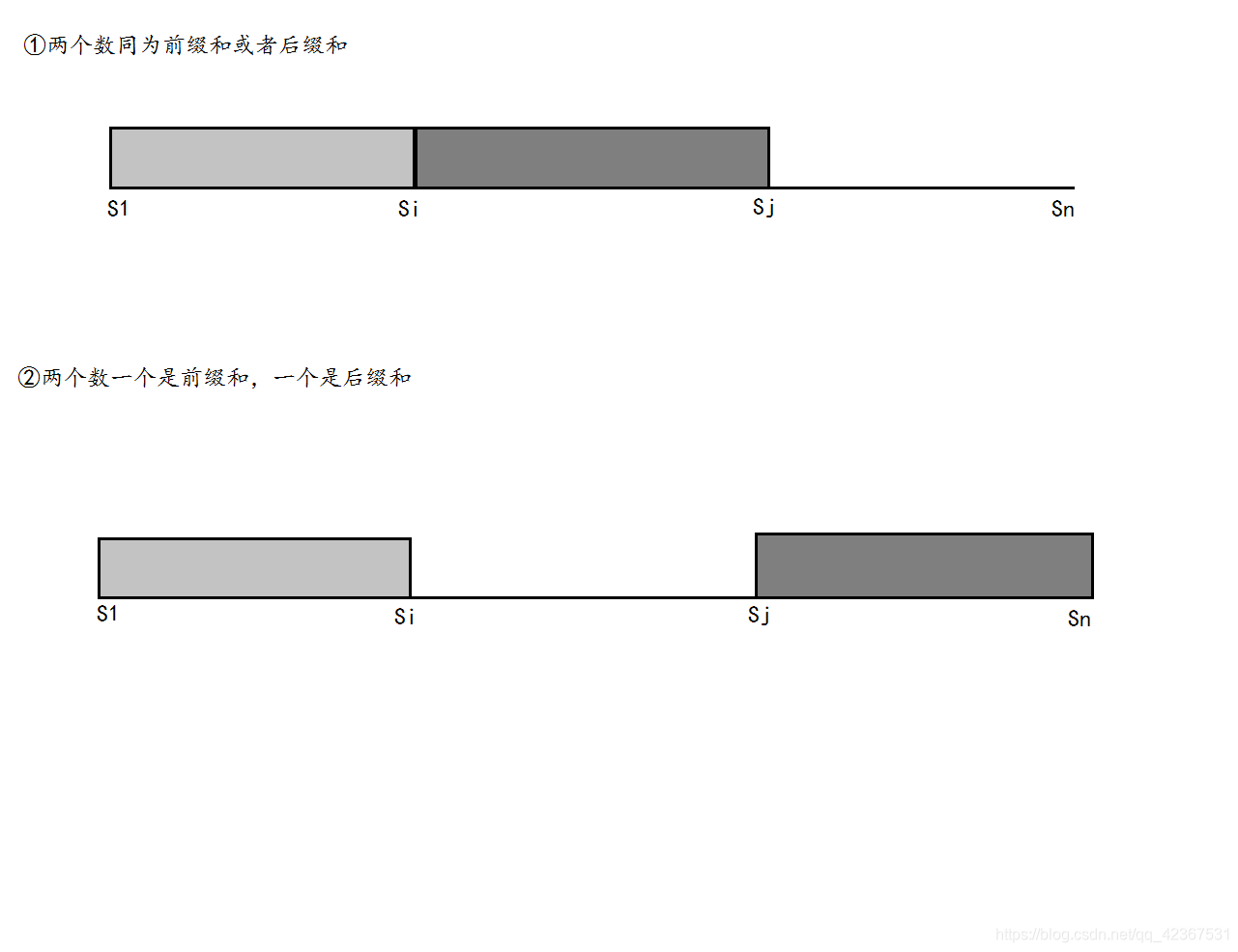
- 当为一种情况时,即都为前缀和或后缀和(后面的前缀和和后缀和统一用 表示,以为我说的是第一种情况),
- 那么 就是位置 的 ,所以我们找到了达成要求的条件,即知道满足 两个 的差值在集合 中,那么就找到了当前正确的
- 凭着是上面的条件,我们可以将枚举 ,并放入相应的位置中,那么他放的可能无非就两种,一是放在左边,二是放在右边,那么枚举时记录一下左右当前位置 和 (即在 范围内都是还没填上数的),一直搜到 ,输出就行,(因为开始我先进行了排序,所以找到的答案一定为最小序列的)
终于说完了~累死了
Code
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <queue>
using namespace std;
//#define int long long
const int manx = 1e7;
const int maxm = 1e8;
const int inf = 0x3f3f3f3f;
int read(){
char c = getchar();int x = 0,f = 1;
for( ;!isdigit(c);c = getchar()) if(c == '-') f = -1;
for( ;isdigit(c);c = getchar()) x = x * 10 + (c ^ 48);
return x * f;
}
int a[manx],ans[manx];
bool vis[manx],flag;
int n, m, i;
void dfs(int k ,int l ,int r ,int sum_l ,int sum_r){
/*
k 表示枚举的数据给出的已经排完序的A[k]
l,r 表示搜到的左右边界(l,r是我们要填数的其中一个,所以记录的都是他们前一个或后一个的和),
sum_l,sum_r 分别记录的是l-1的前缀和,r+1的后缀和,
*/
if(flag == true) return;//完成深搜
if(l == r){
if(vis[a[k] - sum_l] == false && vis[a[k] - sum_r] == false) return;
if( a[2 * n] - sum_l - sum_r < 1 || a[2 * n] - sum_l - sum_r > 500) return; //这里被卡,防止在加数的先选的大的,剩下个小的,之后一相减就成负数了
ans[l] = a[2 * n] - sum_l - sum_r;
for(i = 1;i <= n; i++) printf("%d ",ans[i]);
cout<<'\n';
flag = true;
}
if(vis[a[k] - sum_l] == true ){
ans[l] = a[k] - sum_l;
dfs(k + 1 ,l + 1 ,r ,a[k] ,sum_r);
}
if(vis[a[k] - sum_r] == true ){
ans[r] = a[k] - sum_r;
dfs(k + 1 ,l , r - 1,sum_l , a[k]);
}
}
int main(){
//freopen("dd.in","r",stdin);
//freopen("dd.out","w",stdout);
n = read();
for(i = 1;i <= n * 2;i ++) a[i] = read();
sort(a + 1 ,a + 1 + n * 2);
m = read();
for(i = 1;i <= m; i++) {
int x = read();
vis[x] = true;//表示x这数在不在集合S当中
}
dfs(1,1,n,0,0);
return 0;
}
最累的题解了~
小木棍
题目描述
原题来自:
乔治有一些同样长的小木棍,他把这些木棍随意砍成几段,直到每段的长都不超过 。现在,他想把小木棍拼接成原来的样子,但是却忘记了自己开始时有多少根木棍和它们的长度。给出每段小木棍的长度,编程帮他找出原始木棍的最小可能长度。
思路
首先这是一个非常适合刚学剪枝的同学练习,真的有点小全
题目给的信息里有多个自变量,因此我们就可以想到用深搜进行暴力枚举,不过会
基本暴力思路就是先枚举答案,保证是在当前答案下可以刚好凑成,在此情况下进行深搜就可以了,找的第一个答案就是最小的。
-
对于答案的枚举
找到现在木棍中最长的
表示所有木棍的总长度
这样我们答案一定就在 对不对
for( len = maxx;len <= sum; len++){ if(sum % len != 0) continue; /* 整除才可以作为答案的一种,因为原木棍是整数 */ cnt = sum / len;//cnt 原木棍的数量 memset(vis,0,sizeof(vis)); if(dfs(1,0,1)){ cout << len <<endl; break; } } -
深搜
即正在拼第 根木棒(确保前面的都拼好了)
第 根木棒的当前长度为
拼第 根木棒的上一根小木棒为(有些小朋友可能会有疑问,为什么第一次搜索是 而不是 首先,如果 也能过并且更正确一些,而即使 在 中的第三个
if中,因为v[i]==1也不会进入) -
剪枝
- 对于每根木棒, 记录的是最近一次尝试拼接的木棍长度。这样再回溯时就不会再尝试相同长度的木棍。
- 限制先后加入一根原始木棍的长度是递减的。因为先拼上一个长为 的木棍再拼上一个长为 的木棍,等效于先拼上一个长为 的木棍再拼上一个长为 的木棍。所以只需要搜索其中一种即可。
- 如果在一根原始木棒中尝试拼接的第一根木棍的递归分支就以失败返回,直接判断当前分支无解。
- 如果两个木棍的长度和与一个木棍的一样,只尝试一个的就行了(因为前两个可能会有更大的效用
- 优化搜索顺序,优先尝试较长的木棍。(这就是排序的原因)
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <string.h>
using namespace std;
typedef long long ll;
const int manx=1e6+10;
const int mamx = 1e6 + 11;
const ll mod = 2123400401301379571;
const int inf = 0x3f3f3f3f;
inline int read() {
char c = getchar(); int x = 0, f = 1;
for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
return x * f;
}
int n,a[manx],maxx,sum,cnt,len;
int cmp(int a,int b){
return a > b;
}
int vis[manx];
int dfs(int s,int js,int last){
if(s > cnt) return true;
if(js == len) return dfs(s+1,0,1);
int fail = 0;
for(int i = last;i <= n; i++){//第二剪枝
if(vis[i] == 0 && a[i] + js <= len && fail != a[i]){//第一剪枝
vis[i] = 1;
if(dfs(s,js+a[i],i)) return true;
vis[i] = 0;//还原搜索前的状态。
fail = a[i];//回溯状态,防止i之后的数例在会出现相同的数,剪枝~
if(js == 0 || js + a[i] == len) return false;//第三第四剪枝
}
}
return false;
}
int main(){
n = read();
for(int i = 1;i <= n ; i++){
a[i] = read();
sum += a[i];
maxx = max(maxx,a[i]);
}
sort(a+1,a+1+n,cmp);
for( len = maxx;len <= sum; len++){
if(sum % len != 0) continue;//第五剪枝
cnt = sum / len;
memset(vis,0,sizeof(vis));
if(dfs(1,0,1)){
cout << len <<endl;
break;
}
}
return 0;
}
生日蛋糕
题目描述
要制作一个体积为 的 层生日蛋糕,每层都是一个圆柱体。
设从下往上数第 蛋糕是半径为 ,高度为 的圆柱。当 时,要求 且 。由于要在蛋糕上抹奶油,为尽可能节约经费,我们希望蛋糕外表面(最下一层的下底面除外)的面积 最小。
令 ,请编程对给出的 和 ,找出蛋糕的制作方案(适当的 和 的值),使 最小。(除 外,以上所有数据皆为正整数)
思路
简单的深搜,只需要记录每次的 $H$ 和 $R$ ,依次深搜下去,在进行答案的比较,不过显然这会 $TLE$
因此这也是一个练习剪枝很好的题,
-
当前的奶油面积+之后的最小奶油面积>现在已求出的的最小奶油面积——果断``return`;
-
当前的体积>n,
return; -
当前的体积+之后的最大体积<体积总数,果断
return; -
发现每次枚举半径和高时,是从上一个的半径和高,到还剩下的层数。为什么呢,是因为每一层的半径和高都要比下一层的小1,所以你得每一层都留一个1,,是从上一个的半径和高,到还剩下的层数;
Code
#include <bits/stdc++.h>
using namespace std;
int n, m;
const int manx = 1e6;
int ans = 987654321;
int mins[manx],minv[manx];
inline void dfs(int c,int v, int s,int h,int r) {//层数,半径,高度,体积,抹奶油的外表面积
if(c == 0){
if(v == n) ans = min(ans ,s);
return;
}
if(v + minv[c] > n) return;
if(s + mins[c] > ans) return;
if(s + 2 *(n-v) / r > ans ) return;
for (int i = r - 1; i >= c; --i)
{
if(c == m) s = i * i;
int Maxh = min(h - 1,(n - v - minv[c - 1])/(i * i));
for (int j = Maxh; j >= c; --j)
dfs(c - 1, v + i * i * j, s + 2 * i * j,j,i);
}}
int main() {
scanf("%d%d", &n, &m);
int MaxR = sqrt(n);
for(int i = 1;i <= n; i++){
minv[i] = minv[i-1] + i * i * i;
mins[i] = mins[i-1] + 2 * i * i;
}
// for (int i = m; i <= nn; ++i)//因为有m层,所以第一层至少为m,至多推公式
// for (int j = m; j <= n / (m * m); ++j)//范围也是由体积公式推理而得
// dfs(1, i, j, n, i * i );
dfs(m,0,0,n,MaxR);
if(ans == 987654321)
cout<<0<<endl;
else cout<<ans<<endl;
return 0;
}
本文作者:zxsoul
本文链接:https://www.cnblogs.com/zxsoul/p/14194679.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步