P1064 [NOIP2006 提高组] 金明的预算方案

P1064 [NOIP2006 提高组] 金明的预算方案

在 P1064 [NOIP2006 提高组] 金明的预算方案 这题中，引入了 主件和附件 的关系

比如说

要求你加入集训队试训之前，一定要刷完专题

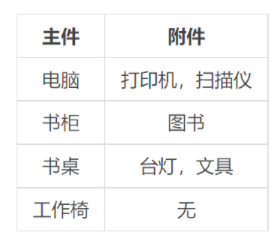
一个主件和它的附件集合是几乎对于分组背包中的一个物品组。

每个选择了主件又选择了若干附件的策略，对应这个物品组的中的一个物品。

题意:

给出每个物品的价格和重要度和是否是主件或者说是谁的附件，求最后选出的每件物品的价格与重要度乘积和的最大值，每个附件不再有附件。

思路:

我们可以将每个附件看成一个01背包问题，这样当我们知道给一个主件分配多少价钱的时候，就可以知道此时这个主件及其附件在对应的价钱可以获得的最大价值。

题目明确了价格以及拥有的钱都是 \(10\) 的倍数，所以这里可以一开始的时候就除以 \(10\) 来降低时间复杂度。

实现:

#include <stdio.h>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 4e3 + 5, M = 65;
vector<int> ve[M];
int wei[M], imp[M];
int n, m;
int f[M][N];
int main()
{
    scanf("%d%d", &m, &n);
    m /= 10;
    for (int i = 1; i <= n; i++)
    {
        int c;
        scanf("%d%d%d", &wei[i], &imp[i], &c);
        wei[i] /= 10;
        ve[c].push_back(i);
    }

    // 先处理给出每个主件分配不同空间时对应获得的最大价值
    //  遍历各主件
    for (int u = 1; u <= n; u++)
    {
        // 01背包问题----(这里滚动了变成了一个维数组)
        // f[u][j] 表示第 u 个背包，分配 j 体积 可以获得的最大价值
        //  遍历附件（物品数量)
        for (int j = 0; j < ve[u].size(); j++)
        {
            int to = ve[u][j];
            for (int k = m; k >= wei[to]; k--)
            {
                f[u][k] = max(f[u][k], f[u][k - wei[to]] + imp[to] * wei[to] * 10);
            }
        }
    }

    // 整合
    // 遍历主件
    for (int i = 0; i < ve[0].size(); i++)
    {
        int to = ve[0][i];
        for (int j = m; j >= wei[to]; j--)
        {
            // 遍历给当前主件的附件分配的空间
            for (int k = j - wei[to]; k >= 0; k--)
            {
                f[0][j] = max(f[0][j], f[to][k] + imp[to] * wei[to] * 10 + f[0][j - k - wei[to]]);
            }
        }
    }
    printf("%d\n", f[0][m]);

    return 0;
}

较一般的题目:

更一般的问题是:

依赖关系以图论中的 "森林" 形式给出，也就是说主件的附件依旧可以有自己的附件集合。

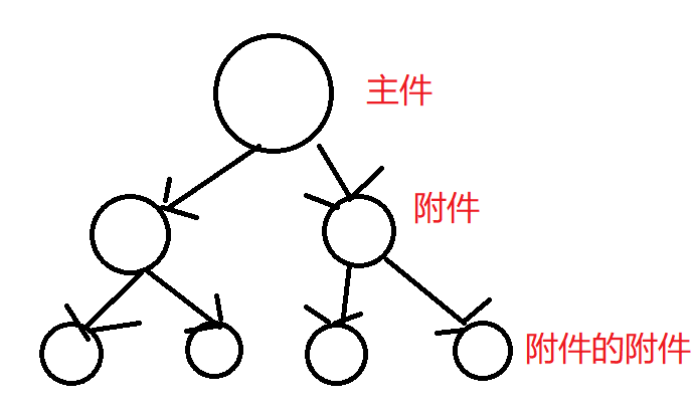
刚刚那道题可以直接那么做，主要是因为附件没有附件，如果还有附件的话，就需要继续先计算出附件在面对各价格时可获得的最大值才可以。

这种背包就是 树形背包 （树形dp的一种），它的特点是每个父节点都需要对它的各个耳机的属性进行一次 dp 来求得自己相关的属性。

比如刚刚那道题还可以写成如下形式:

#include <stdio.h>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 4e3 + 5, M = 65;
vector<int> ve[M];
int wei[M], imp[M];
int n, m;
int f[M][N];
void dfs(int u)
{
    //枚举物品
    for (int i = 0; i < ve[u].size(); i++)
    {
        int to = ve[u][i];
        dfs(to);
        for (int j = m; j >= 0; j--)
        {
            //枚举分给当前物品的体积(不包括当前物品的体积)
            for (int k = j; k >= 0; k--)
            {
                if (k - wei[to] >= 0)
                    f[u][j] = max(f[u][j], f[u][j - k] + f[to][k - wei[to]] + imp[to] * wei[to] * 10);
                else
                    break;
            }
        }
    }
}

int main()
{
    scanf("%d%d", &m, &n);
    m /= 10;
    for (int i = 1; i <= n; i++)
    {
        int c;
        scanf("%d%d%d", &wei[i], &imp[i], &c);
        wei[i] /= 10;
        ve[c].push_back(i);
    }
    dfs(0);
    int res = 0;
    res = f[0][m];
    printf("%d\n", res);
    return 0;
}