P1757 通天之分组背包
P1757 通天之分组背包
有 \(N\) 件物品和一个容量为 \(V\) 的背包。第 \(i\) 件物品的费用是 \(C_i\) ,价值是 \(W_i\) 。这些物品被划分为 \(K\) 组,每组中的物品互相冲突,最多选一件。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
思路:
将同一组的物品整合起来,称为一个大物品,那么问题就变成了若干个大物品中,每个可以选择其中的一个物品,求总费用不超过限制的价值最大值是多少?
其实可以发现,这个非常的类似多重背包。
定义 \(f[i][j]\) 为遍历到第 \(i\) 个大物品,当前体积不超过 \(j\) 的价值最大值是多少?
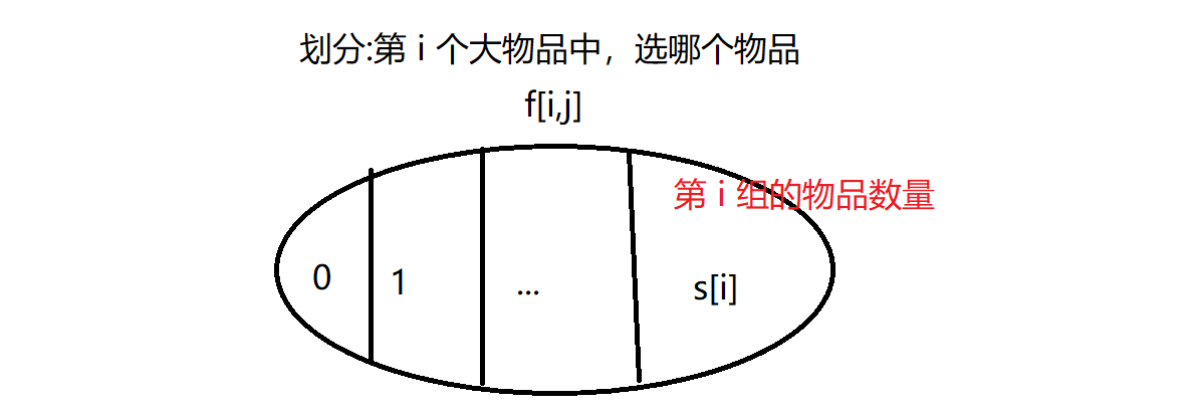
实现:
#include <stdio.h>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 1005;
int f[N][N], q[N];
struct node
{
int wei, val;
node(int a, int b)
{
wei = a, val = b;
}
};
vector<node> ve[N];
int main()
{
int n, m;
scanf("%d%d", &m, &n);
int we = 0;
for (int i = 1; i <= n; i++)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
ve[c].push_back(node(a, b));
we = max(we, c);
}
for (int i = 0; i <= we; i++)
for (int j = 0; j <= m; j++)
f[i][j] = -1e9;
f[0][0] = 0;
// 遍历物品
for (int i = 1; i <= we; i++)
{
// 遍历体积
for (int j = 0; j <= m; j++)
{
// 遍历决策
f[i][j] = f[i - 1][j];
for (int k = 0; k < ve[i].size(); k++)
{
if (ve[i][k].wei <= j)
f[i][j] = max(f[i][j], f[i - 1][j - ve[i][k].wei] + ve[i][k].val);
}
}
}
int res = 0;
for (int i = 0; i <= m; i++)
res = max(res, f[we][i]);
printf("%d\n", res);
return 0;
}

