cf 189A Cut Ribbon
cf 189A Cut Ribbon
题意:
给一长度为 \(n\) 的钢条,要求将其剪成若干长度为 \(p, q, r\) 的短条,且短条数量尽可能多。
裁出的长度只能是 \(p,q,r\)不能有其他长度。要求恰好裁完,保证答案存在。
思路:
\(f[i]\) 表示的是当空间为 \(i\) 的时候有多少种方法放满。
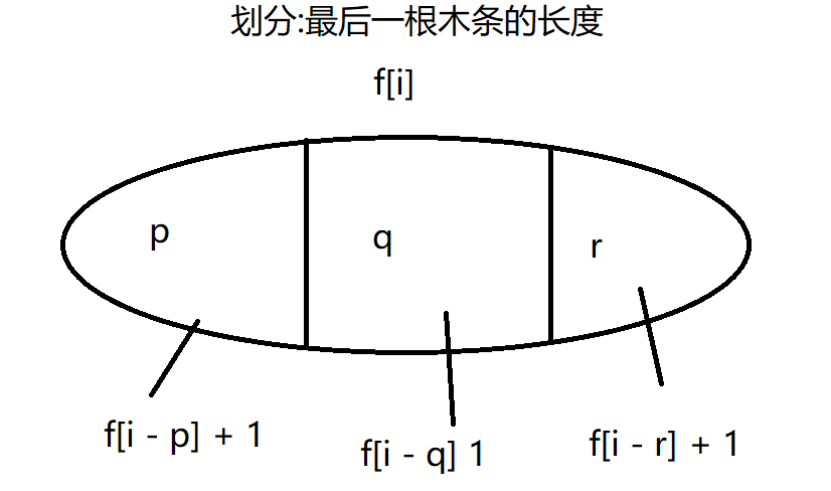
状态转移方程:
\(f[i] = max(f[i - p] + 1,f[i - q] + 1,f[i - r] + 1)\) (如果对应 \(f[i - ?]\) 存在)
实现:
#include <bits/stdc++.h>
using namespace std;
const int N = 4e3 + 5;
int a[4], f[N];
int main()
{
int n;
scanf("%d", &n);
for (int i = 1; i <= 3; i++)
scanf("%d", &a[i]);
f[0] = 1;//方便标记哪些长度是已经凑出来的
for (int i = 1; i <= n; i++)
for (int j = 1; j <= 3; j++)
{
if (i >= a[j] && f[i - a[j]])
f[i] = max(f[i], f[i - a[j]] + 1);
}
printf("%d\n", f[n] - 1);
return 0;
}

