P1616 疯狂的采药

P1616 疯狂的采药

给出可以采药的时间 \(t\) ,和草药的数目 \(m\) ，每种草药需要的时间以及价值，每种草药采的数量不限。求再时间范围内能求到的草药的最大价值是多少?

思路:

状态定义和上一题一样

\(f[i][j]\) :遍历到第 \(i\) 个物品，且体积不超过 \(j\) 时可以获得的最大价值

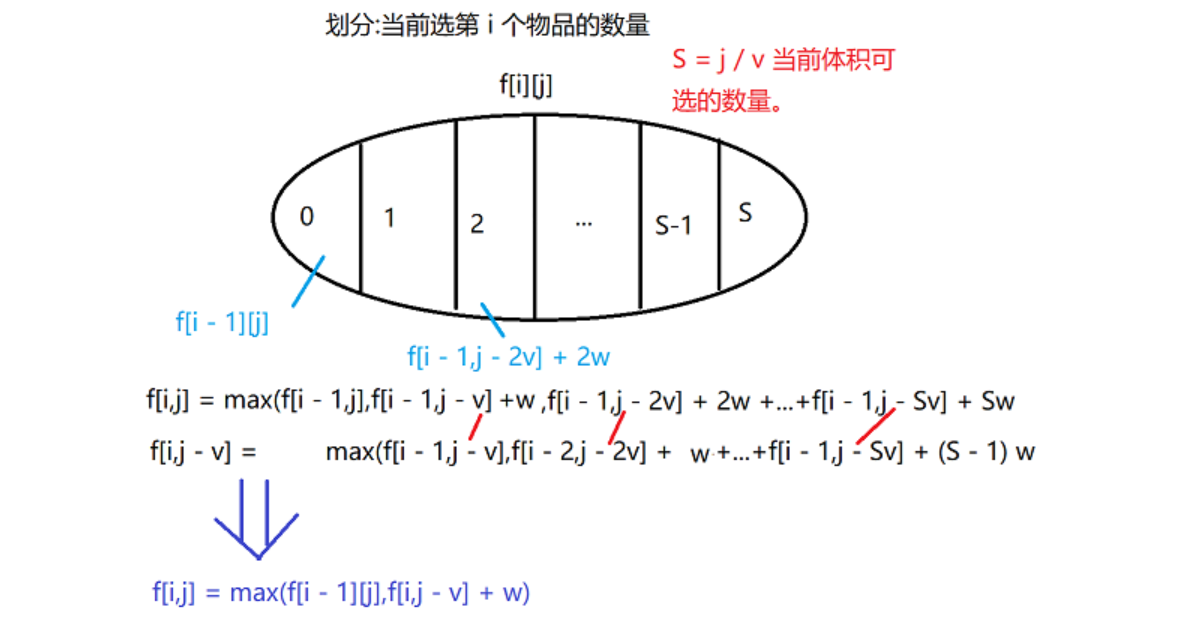
用第一种方法的话，就是

for 物品
    for 体积
        for 决策

时间复杂度是 \(O(N * M * M)\)

第二种方法的话

\(f[i,j] = max(f[i - 1][j],f[i][j - v] + w)\)

上面的方法用到了 \(f[i][j - v]\) 所以决定了第二层必须正序遍历。

然后可以发现这里涉及到 \(f[i - 1]\) 的，只涉及到 \(f[i - 1][j]\) ，所以也可以滚动掉一个维度

实现:

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 5;
typedef long long ll;
int w[N], v[N];
int main()
{
    int t, m;
    scanf("%d%d", &t, &m);
    vector<ll> f(t + 1,0);
    for (int i = 1; i <= m; i++)
        scanf("%d%d", &w[i], &v[i]);
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= t; j++)
        {
            if (j >= w[i])
                f[j] = max(f[j], f[j - w[i]] + v[i]);
        }
    printf("%lld\n",f[t]);
    return 0;
}