P2758 编辑距离

1|0P2758 编辑距离

题意:

设 $A$ 和 $B$ 是两个字符串。我们要用最少的字符串操作次数，讲字符串 $A$ 转换为字符串 $B$ ，这里所说的字符操作共有三种:

• 删除一个字符
• 插入一个字符
• 将一个字符定义成另一个字符

$A,B$ 均只包含小写字母。

思路:

状态定义?

涉及到两个字符是否相等，所以我们需要现在匹配到的确切位置，所以定义 $f[i][j]$ 为将字符串 $A,1-i$ 匹配到字符串 $B,1-j$ 需要的最少操作次数。

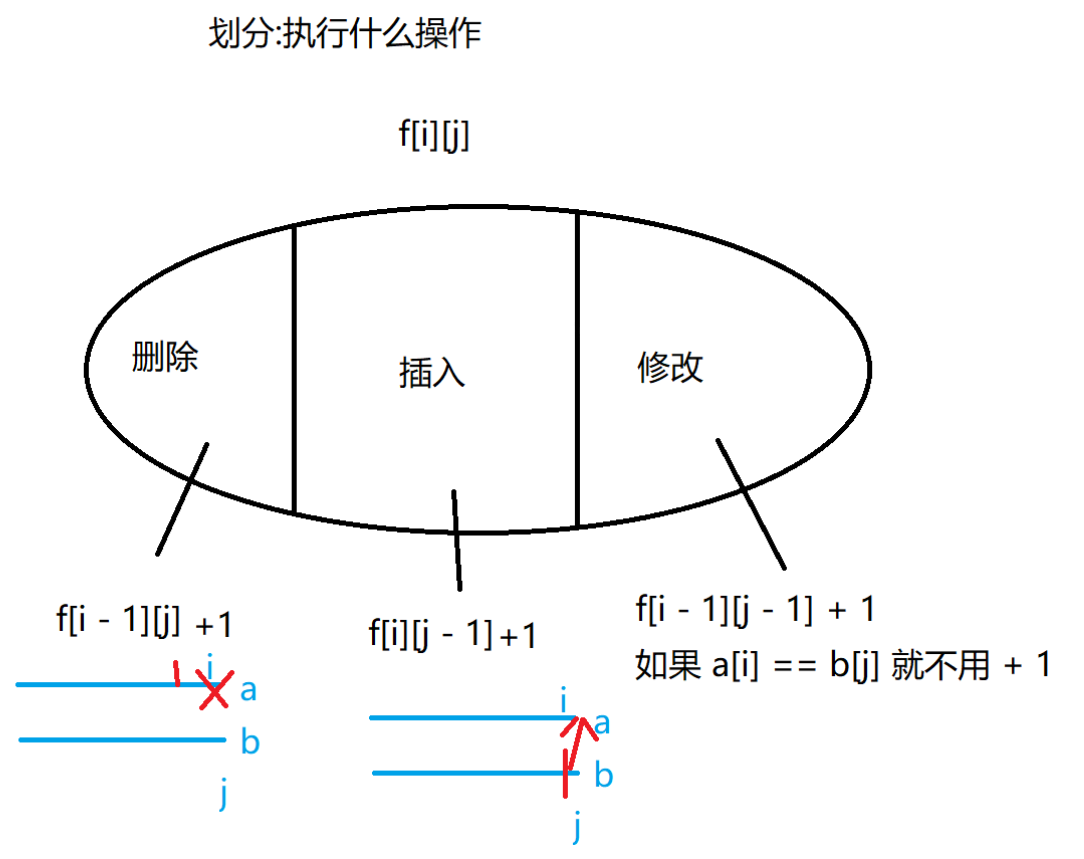
转移方程:

$f[i][j]=min(f[i-1][j]+1,f[i][j-1]+1)$

$f[i][j]=min(f[i][j],f[i-1][j-1]+a[i]!=a[j])$

实现:

#include <bits/stdc++.h>
using namespace std;
const int N = 2e3 + 5;
int f[N][N];
char a[N], b[N];
int main()
{
    scanf("%s", a + 1);
    scanf("%s", b + 1);
    int n = strlen(a + 1), m = strlen(b + 1);
    for (int i = 1; i <= n; i++)
        f[i][0] = i;
    for (int i = 1; i <= m; i++)
        f[0][i] = i;

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
        {
            f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;
            if (a[i] == b[j])
                f[i][j] = min(f[i][j], f[i - 1][j - 1]);
            else
                f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
        }
    printf("%d\n", f[n][m]);

    return 0;
}

__EOF__

本文作者：zxr
本文链接：https://www.cnblogs.com/zxr000/p/16997804.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！