POJ-2533 Longest Ordered Subsequence
POJ-2533 Longest Ordered Subsequence
题意:
给出一个序列,求出这个序列的最长上升子序列
序列 \(A\) 的上升子序列 \(B\) 定义如下:
- \(B\) 为 \(A\) 的子序列
- \(B\) 为严格递增序列
思路:
状态定义?
定义 \(f[i]\) 为遍历到 \(i\) 的最长上升子序列?我们要知道当前 \(a[i]\) 是否能放入一个子序列中,需要知道那个子序列的最后一个数字是多少,所以显然不能这么定义。
那怎么定义可以知道之前的子序列的最后一个数字是多少呢?
定义 \(f[i]\) 为以第 \(i\) 个为最后一个元素的子序列的最大值。
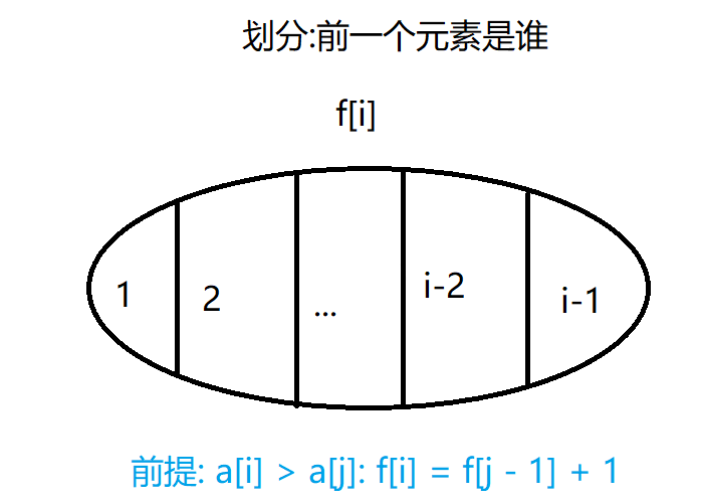
转移方程:
\(if(a[i] > a[j])\)
\(f[i] = f[j - 1] + 1\)
实现:
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e3 + 5;
int a[N], f[N];
int main()
{
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
int res = 0;
for (int i = 1; i <= n; i++)
{
f[i] = 1; // 自己可以作为一个子序列
for (int j = 1; j < i; j++)
{
if (a[i] > a[j])
f[i] = max(f[i], f[j] + 1);
}
res = max(res, f[i]);
}
printf("%d\n", res);
return 0;
}

