POJ-1458 Common Subsequence
POJ-1458 Common Subsequence
题意:
首先对最长子序列有个定义:如果一个字符串a可以由另一个字符串b删去某些元素得到,那么说明a就是b的子序列字符串
现在有两个字符串,请问最长公共子序列是多长?
思路:
状态定义?
需要知道当前两个字符串比较到哪里了 \(\Rightarrow\) 定义 \(f[i][j]\) 字符串 \(a\) 遍历到第 \(i\) 个点,字符串 \(b\) 遍历到第 \(j\) 个点时,该状态的最长公共子序列是多长。
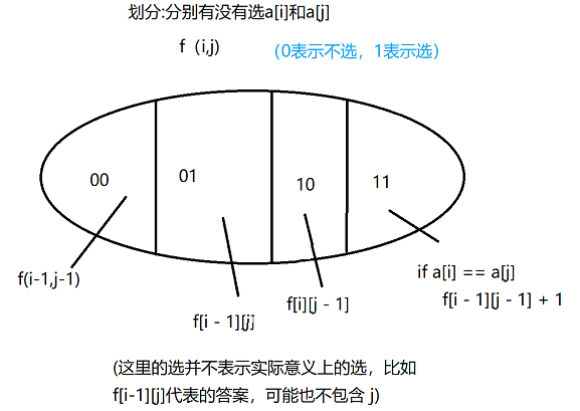
实现:
#include <cstdio>
#include <algorithm>
#include <string>
#include <iostream>
using namespace std;
const int N = 1e3 + 5;
int f[N][N];
int main()
{
string a, b;
while (cin >> a >> b)
{
a = '0' + a, b = '0' + b;
for (int i = 1; i < a.size(); i++)
for (int j = 1; j < b.size(); j++)
f[i][j] = 0;
for (int i = 1; i < a.size(); i++)
for (int j = 1; j < b.size(); j++)
{
if (a[i] == b[j])
f[i][j] = f[i - 1][j - 1] + 1;
else
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
}
printf("%d\n", f[a.size() - 1][b.size() - 1]);
}
return 0;
}

