北京清北 综合强化班 Day1
a
【问题描述】
你是能看到第一题的 friends呢。
—— hja
何大爷对字符串十分有研究,于是天出题虐杀 zhx。何大爷今天为 何大爷今天为 字符串定义了新的权值计算方法。一个由小写母组成,被定义为其中出现次数最多的字符减去少。(注 被定义为其中出现次数最多的字符减去少。(注 意,在讨论出现最少的字符时候该必须至一次)何大爷给你一个字符串,何大爷想知道这的所有子中权值最是多少?
【输入格式】
第一行一个整数n,代表字符串的长度。
接下来一行n个小写字母,代表该字符串。
【输出格式】
一行个整数代表答案。
【样例输入】
10
aabbaaabab
【样例输出】
3
【数据范围与规定】
对于 30%的数据, 1≤n≤100。
对于 60%的数据, 1≤n≤1000。
对于 100%的数据, 1≤n≤106.
题目大意:
求一个字符串子串的最多出现次数 减去 最少出现次数的 最大值
思路:
1.爆搜
2.正解:前缀和进行求解
枚举右端点,使用前缀和优化。
加入我们选定一段区间l~r,并且假设出现次数最多的为x,最少的为z,用一个数组sum[]统计一个字母到当前位置出现的次数,那么出现次数最多的字母与最少字母的差值显然为:
sum[x][r]-sum[x][l-1]-(sum[z][r]-sum[z][l-1])
==> sum[x][r]-sum[z][r]-sum[x][l-1]+sum[z][l-1]
==> (sum[x][r]-sum[z][r])-(sum[x][l-1]-sum[z][l-1])
然后你可以发现:前面括号中的跟后面括号中的本质上是一个东西的,长的一毛一样,只是后面的区间端点不同而已。
但是又因为l-1一定是比r要小的,所以l-1一定会在枚举r之前就已经被处理出来;
所以现在我们需要知道的就只有x和z到底是谁就ok:
我们枚举每一个点,然后再枚举另一个字母,处理出最大的sum[x][r]-sum[z][r](r是我们要枚举的位置,x是这个位置上的字母,y是枚举的另一字母)。
用来更新最大值,这样的话我们枚举出来的字母就会出现两种情况,要么x比z多,要么z比x多。
所以我们取一个最大值来更新答案,又因为这里的sum[x][l-1]-sum[y][l-1]是前面预处理出来的,所以每次在枚举到的位置取一最小值储存一下,并且记录是在什么时候更新的这个最小值。
并且还要注意的是:
当last[j]==(pos[j][now] || pos[now][j])时,如果减去的话就会直接把j这个字母消去,所以在后半段我们需要把这个多减去的1加上。
后面一部分是加没错了,可是对于前面来说就是减去1,因为(sum[x][r]-sum[z][r])-(sum[x][l-1]-sum[z][l-1])嘛!
上代码:

#include <iostream> #include <cstring> #include <cstdio> #define INF 0x7fffffff using namespace std; const int Ms = 1011; const int Ys = 26; int n,ans,p,maxx,minn=INF; char sr[Ms]; int s[Ys]; int max(int a,int b) { return a > b ? a : b; } int dfs(int op,int ed,int now) { if(ed==n) return ans; s[now]++; maxx=0,minn=INF; for(int i=0; i<Ys; ++i) { if(s[i]==0) continue; if(s[i]>maxx) maxx=s[i]; if(s[i]<minn) minn=s[i]; } if(maxx-minn>ans) ans=maxx-minn; ed++; dfs(op,ed,sr[ed]-97); } int main() { freopen("a.in","r",stdin); freopen("a.out","w",stdout); scanf("%d",&n); for(int i=0; i<n; ++i) cin>>sr[i]; for(int i=0; i<n; ++i) { p=max(p,dfs(i,i,sr[i]-97)); memset(s,0,sizeof(s)); maxx=0,minn=INF,ans=0; } printf("%d",p); return 0; }

#include <iostream> #include <cstdio> #include <cmath> using namespace std; const int N = 26; const int M = 1000001; char ch[M]; int n,now,ans; int sum[N],last[N],pos[N][N],minn[N][N]; int main() { scanf("%d",&n); cin>>ch+1; //从1开始输入 for(int i=1; i<=n; ++i) { now=ch[i]-'a'; last[now]=i; //枚举的这段距离中now最后一次出现的位置 sum[now]++; //记录出现次数 for(int j=0; j<N; ++j) if(now!=j && sum[j]) { int tmp=ans; ans=max(sum[now]-sum[j]-minn[now][j]-(last[j]==pos[now][j]), sum[j]-sum[now]-minn[j][now]-(last[j]==pos[j][now])); ans=max(ans,tmp); } for(int j=0; j<N; ++j) { if(sum[now]-sum[j]<minn[now][j]) minn[now][j]=sum[now]-sum[j],pos[now][j]=i; if(sum[j]-sum[now]<minn[j][now]) minn[j][now]=sum[j]-sum[now],pos[j][now]=i; } } printf("%d\n",ans); return 0; }
b
【问题描述】
你是能看到第二题的 friends呢。
—— laekov
Hja和 Yjq在玩捉迷藏。 在玩捉迷藏。 Yjq躲了起来, Hja要找他。
在们玩游戏的房间 里,只有一堵不透明的墙和个双面镜子。 Hja和 Yjq可以看作平面上坐标分 别为 (xv,yv)和(xp,yp)的点。
墙是一条连接 (xw1,yw1)和(xw2,yw2)的线段,镜子是一条连接 (xm1,ym1)和(xm2,ym2)的线段。
如果 视线和障碍物有公共点,那么我们认为会被阻挡,无法看见。
如果视线和镜子有公共点,那么我们认为发生了反射。
反射的过程遵循物理规律 —— 入射角等于反射角,且反射光线与入射光线在镜子同侧。
也就是说想要看见对方, Hja和 Yjq必须在镜子的同一侧,包括所直线上(参见样例1)。
如果 视线与镜子重合,那么不会发生反射,并且被当作障碍物(参见样例4)。
Hja很想知道他站在原地能否看见 Yjq,,帮助他解决这个问题。
【输入格式】
第一行两个数 xv,yv,表示 Hja的坐标。
第二行两个数 xp,yp,表示 Yjq的坐标。
第三行四个数 xw1,yw1,xw2,yw2,分别表示墙的两个端点坐标。
第四行四个数 xm1,ym1,xm2,ym2,分别表示镜子的两个端点坐标。
【输出格式】
如果 Hja站在原地能看到 Yjq,则输出 "YES",否则输出 "NO"。
【样例输入1】
-1 3
1 3
0 2 0 4
0 0 0 1
【样例输出1】
NO
【样例输入2】
0 0
1 1
0 1 1 0
-100 -100 -101 -101
【样例输出2】
NO
【样例输入3】
0 0
1 1
0 1 1 0
-1 1 1 3
【样例输出3】
YES
【数据规模与约定】
对于100%的数据,所有坐标均为绝对值不超过10 4 的整数。输入的线段不会退化成点,且两条线段没有交点。Hja 和 Yjq 的位置不同,且不在任何一条线段上。
思路:
据说是最简单的计算几何呢(OvO)
我悄悄的告诉你:
其实输出YES有46分233,输出NO就更多了!有54分!
这题我选择弃疗qwq
上代码:

#include<cstdio> #include<cstdlib> #include<cstring> #include<cmath> #include<algorithm> using namespace std; const double eps=1e-8; int sgn(double a) { if (fabs(a)<eps) return 0; else { if (a>0.0) return 1; else return -1; } } struct point { double x,y; point() {} point(double a,double b) { x=a; y=b; } void init() { scanf("%lf%lf",&x,&y); } point operator+(const point &a)const { point ans; ans.x=x+a.x; ans.y=y+a.y; return ans; } point operator-(const point &a)const { point ans; ans.x=x-a.x; ans.y=y-a.y; return ans; } point operator*(const double &a)const { point ans; ans.x=x*a; ans.y=y*a; return ans; } void print() { printf("%lf %lf\n",x,y); } } v,p,w1,w2,m1,m2; double cross(point a,point b) { return a.x*b.y-a.y*b.x; } double dot(point a,point b) { return a.x*b.x+a.y*b.y; } bool cross(point p1,point p2,point p3,point p4) { if (sgn(cross(p2-p1,p3-p1))*sgn(cross(p2-p1,p4-p1))==1) return false; if (sgn(cross(p4-p3,p1-p3))*sgn(cross(p4-p3,p2-p3))==1) return false; if (sgn(max(p1.x,p2.x)-min(p3.x,p4.x))==-1) return false; if (sgn(max(p1.y,p2.y)-min(p3.y,p4.y))==-1) return false; if (sgn(max(p3.x,p4.x)-min(p1.x,p2.x))==-1) return false; if (sgn(max(p3.y,p4.y)-min(p1.y,p2.y))==-1) return false; return true; } point getcross(point p1,point p2,point p3,point p4) { double a=p2.y-p1.y; double b=p1.x-p2.x; double c=-p1.x*p2.y+p1.y*p2.x; double d=p4.y-p3.y; double e=p3.x-p4.x; double f=-p3.x*p4.y+p3.y*p4.x; double x=(b*f-c*e)/(a*e-b*d); double y=(a*f-c*d)/(b*d-a*e); return point(x,y); } point calcfoot(point p1,point p2,point p3) { double ratio=dot(p1-p2,p3-p2)/dot(p3-p2,p3-p2); return p2+(p3-p2)*ratio; } bool check() { if (!cross(v,p,w1,w2)) { if (!cross(v,p,m1,m2)) return true; if (sgn(cross(m1-v,m2-v))==0 && sgn(cross(m1-p,m2-p)==0)) return true; } if (sgn(cross(m2-m1,v-m1))*sgn(cross(m2-m1,p-m1))==1) { point foot=calcfoot(p,m1,m2); foot=foot*2.0-p; if (cross(v,foot,m1,m2)) { foot=getcross(v,foot,m1,m2); if (!cross(v,foot,w1,w2) && !cross(foot,p,w1,w2)) return true; } } return false; } int main() { freopen("b.in","r",stdin); freopen("b.out","w",stdout); v.init(); p.init(); w1.init(); w2.init(); m1.init(); m2.init(); if (check()) printf("YES\n"); else printf("NO\n"); return 0; }
c
【问题描述】
你是能看到第三题的 friends呢。
—— aoao
众所周知,八数码问题是一个非常难的问题,但是Yjq非常有面子,他把这道题简化了一番。现在给了你一个3×3的方格图,你的目标是通过不断移动使得相邻颜色的块形成联通块。你每次的移动方式是选择一列或者一行进行置换滑动(这个解释起来比较麻烦,看下面的图就懂了)。所谓置换滑动,就是所有格子沿着给定的方向顺次移动,最后一个格子会被置换到最前面的过程。现在给定整个方格图,以及每个格子是否能够移动,求使得相同颜色联通的最小步数。
【输入格式】
输入为3×3的方格图,每个位置由五个字符组成,前四个字符分别表示上下左右四个部分的颜色,第五个字符表示该格子是否能够移动,其中0是能移动1是不能移动。
【输出格式】
一行个整数代表答案。

思路:
bfs+并查集
(可以把3*3的矩阵转换为6*6的点阵来进行做,查看是否连通)
还需要注意的是储存颜色!
题目意思:
红线==>蓝线+紫线+橙线
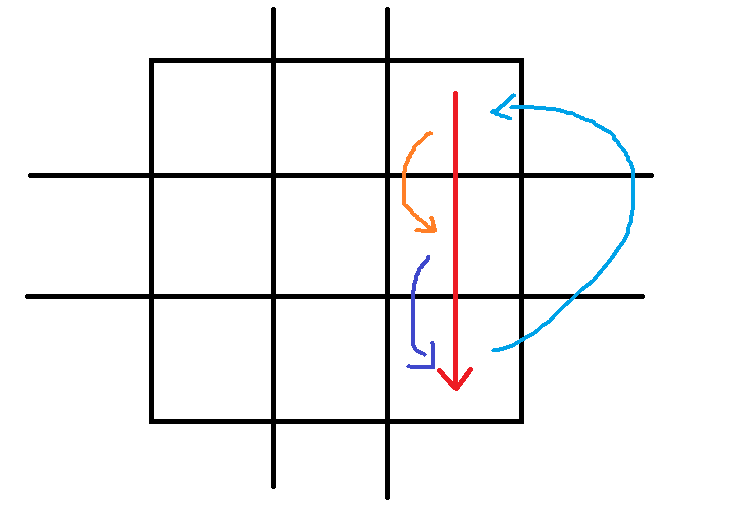
注意:
存有精度的数的时候,
一定要使用double,
别使用float!!!
float太坑了、、、
上代码:

#include<cstdio> #include<cstdlib> #include<cstring> #include<queue> #define get(a,b,c) ((a-1)*12+(b-1)*4+c) using namespace std; int en,tmp[4][4],color[37],map[9][5],q[37],nowmap[4][4],newmap[4][4]; bool num[9],use[90000000],right[37],row[4],col[4],col_find[5]; char s[10]; struct rec { int sta,step; rec() {} rec(int a,int b) { sta=a; step=b; } }; queue<rec> que; struct edge { int e; edge *next; }*v[37],ed[100]; void add_edge(int s,int e) { en++; ed[en].next=v[s]; v[s]=ed+en; v[s]->e=e; en++; ed[en].next=v[e]; v[e]=ed+en; v[e]->e=s; } bool check(int nows) { memset(num,false,sizeof(num)); for(int a=3; a>=1; a--) for(int b=3; b>=1; b--) if(a!=3 || b!=3) { tmp[a][b]=nows%10; num[nows%10]=true; nows/=10; } for(int a=0; a<9; a++) if(!num[a]) { tmp[3][3]=a; break; } int cnt=0; for(int a=1; a<=3; a++) for(int b=1; b<=3; b++) for(int c=1; c<=4; c++) { cnt++; color[cnt]=map[tmp[a][b]][c]; } memset(right,false,sizeof(right)); memset(col_find,false,sizeof(col_find)); for(int a=1; a<=36; a++) if(!right[a]) { if(col_find[color[a]]) return false; col_find[color[a]]=true; int front=1,tail=1; q[1]=a; right[a]=true; for( ; front<=tail; ) { int now=q[front++]; for(edge *e=v[now]; e; e=e->next) if(color[e->e]==color[now] && !right[e->e]) { right[e->e]=true; q[++tail]=e->e; } } } return true; } int main() { freopen("c.in","r",stdin); freopen("c.out","w",stdout); for(int a=1; a<=3; a++) for(int b=1; b<=3; b++) { add_edge(get(a,b,1),get(a,b,3)); add_edge(get(a,b,1),get(a,b,4)); add_edge(get(a,b,2),get(a,b,3)); add_edge(get(a,b,2),get(a,b,4)); if (a!=3) add_edge(get(a,b,2),get(a+1,b,1)); if (b!=3) add_edge(get(a,b,4),get(a,b+1,3)); } int cnt=0; for(int a=1; a<=3; a++) for(int b=1; b<=3; b++) { scanf("%s",s+1); for(int c=1; c<=4; c++) if(s[c]=='R') map[cnt][c]=0; else { if(s[c]=='G') map[cnt][c]=1; else { if(s[c]=='B') map[cnt][c]=2; else map[cnt][c]=3; } } if(s[5]=='1') row[a]=col[b]=true; cnt++; } int nows=1234567; if (check(nows)) { printf("0\n"); return 0; } que.push(rec(nows,0)); use[nows]=true; rec now; while (que.size()) { now=que.front(); que.pop(); int step=now.step; int nows=now.sta; memset(num,false,sizeof(num)); for(int a=3; a>=1; a--) for(int b=3; b>=1; b--) if(a!=3 || b!=3) { nowmap[a][b]=nows%10; num[nows%10]=true; nows/=10; } for(int a=0; a<9; a++) if(!num[a]) { nowmap[3][3]=a; break; } int news=0; for(int a=1; a<=3; a++) { if(!row[a]) { for(int b=1; b<=3; b++) for(int c=1; c<=3; c++) newmap[b][c]=nowmap[b][c]; int x=newmap[a][1]; newmap[a][1]=newmap[a][2]; newmap[a][2]=newmap[a][3]; newmap[a][3]=x; news=0; for (int b=1; b<=3; b++) for (int c=1; c<=3; c++) if (b!=3 || c!=3) news=news*10+newmap[b][c]; if (!use[news]) { use[news]=true; if (check(news)) { printf("%d\n",step+1); return 0; } que.push(rec(news,step+1)); } x=newmap[a][1]; newmap[a][1]=newmap[a][2]; newmap[a][2]=newmap[a][3]; newmap[a][3]=x; news=0; for (int b=1; b<=3; b++) for (int c=1; c<=3; c++) if (b!=3 || c!=3) news=news*10+newmap[b][c]; if (!use[news]) { use[news]=true; if (check(news)) { printf("%d\n",step+1); return 0; } que.push(rec(news,step+1)); } } if(!col[a]) { for(int b=1; b<=3; b++) for(int c=1; c<=3; c++) newmap[b][c]=nowmap[b][c]; int x=newmap[1][a]; newmap[1][a]=newmap[2][a]; newmap[2][a]=newmap[3][a]; newmap[3][a]=x; news=0; for(int b=1; b<=3; b++) for(int c=1; c<=3; c++) if(b!=3 || c!=3) news=news*10+newmap[b][c]; if(!use[news]) { use[news]=true; if(check(news)) { printf("%d\n",step+1); return 0; } que.push(rec(news,step+1)); } x=newmap[1][a]; newmap[1][a]=newmap[2][a]; newmap[2][a]=newmap[3][a]; newmap[3][a]=x; news=0; for(int b=1; b<=3; b++) for(int c=1; c<=3; c++) if(b!=3 || c!=3) news=news*10+newmap[b][c]; if(!use[news]) { use[news]=true; if(check(news)) { printf("%d\n",step+1); return 0; } que.push(rec(news,step+1)); } } } } return 0; }

#include <iostream> #include <cstdio> #include <cstring> #include <queue> #define get(i,j,k) ((i-1)*12+(j-1)*4+k) using namespace std; const int D = 37; const int T = 4; const int Fx = 5; const int Nine = 9; int tmpmap[T][T],color[D],q[D]; int map[Nine][Fx],nowmap[T][T],nxtmap[T][T]; bool num[Nine],vis[Nine*10000000],ok[D]; bool row[T],col[T],Findcol[Fx]; char s[10]; struct rec { int op,step; //起点,步数 rec() {} rec(int a,int b) { op=a; step=b; } }; queue <rec> que; struct edge { int to,next; } e[100]; int top,head[D]; void Add(int u,int v) { top++; e[top].to=v,e[top].next=head[u],head[u]=top; top++; e[top].to=u,e[top].next=head[v],head[v]=top; } bool check(int nows) { memset(num,false,sizeof(num)); for(int i=3; i>=1; --i) for(int j=3; j>=1; --j) if(i!=3 || j!=3) { tmpmap[i][j]=nows%10; num[nows%10]=true; nows/=10; } for(int i=0; i<Nine; ++i) //(压维)处理最后一位数字 if(!num[i]) { tmpmap[3][3]=i; break; } int cnt=0; for(int i=1; i<T; ++i) for(int j=1; j<T; ++j) for(int k=1; k<Fx; ++k) { cnt++; color[cnt]=map[tmpmap[i][j]][k]; //按顺序记录颜色 } memset(ok,false,sizeof(ok)); memset(Findcol,false,sizeof(Findcol)); for(int i=1; i<D; ++i) if(!ok[i]) { if(Findcol[color[i]]) return false; Findcol[color[i]]=true; int h=1,t=1; q[t]=i; ok[i]=true; while(h<=t) { int u=q[h++]; for(int j=head[u]; j; j=e[j].next) { int v=e[j].to; if(color[v]==color[u] && !ok[v]) { ok[v]=true; q[++t]=v; } } } } return true; } int main() { for(int i=1; i<T; ++i) for(int j=1; j<T; ++j) { Add(get(i,j,1),get(i,j,3)); Add(get(i,j,1),get(i,j,4)); Add(get(i,j,2),get(i,j,3)); Add(get(i,j,2),get(i,j,4)); if(i!=3) Add(get(i,j,2),get(i+1,j,1)); if(j!=3) Add(get(i,j,4),get(i,j+1,3)); } int cnt=0; for(int i=1; i<T; ++i) for(int j=1; j<T; ++j) { scanf("%s",s+1); for(int k=1; k<Fx; ++k) if(s[k]=='R') map[cnt][k]=0; else { if(s[k]=='G') map[cnt][k]=1; else { if(s[k]=='B') map[cnt][k]=2; else map[cnt][k]=3; } } if(s[5]=='1') row[i]=col[j]=true; //固定 cnt++; } int nows=1234567; if(check(nows)) { printf("0\n"); return 0; } que.push(rec(nows,0)); vis[nows]=true; rec now; while(!que.empty()) { now=que.front(); que.pop(); int step=now.step,nows=now.op; memset(num,false,sizeof(num)); for(int i=3; i>=1; --i) for(int j=3; j>=1; --j) if(i!=3 || j!=3) { nowmap[i][j]=nows%10; num[nows%10]=true; nows/=10; } for(int i=0; i<Nine; ++i) //(压维)处理最后一位数字 if(!num[i]) { nowmap[3][3]=i; break; } int nxt=0; for(int i=1; i<T; ++i) { if(!row[i]) { for(int j=1; j<T; ++j) for(int k=1; k<T; ++k) nxtmap[j][k]=nowmap[j][k]; int tmp=nxtmap[i][1]; nxtmap[i][1]=nxtmap[i][2]; nxtmap[i][2]=nxtmap[i][3]; nxtmap[i][3]=tmp; nxt=0; for(int j=1; j<T; ++j) for(int k=1; k<T; ++k) if(j!=3 || k!=3) nxt=nxt*10+nxtmap[j][k]; if(!vis[nxt]) { vis[nxt]=true; if(check(nxt)) { printf("%d\n",step+1); return 0; } que.push(rec(nxt,step+1)); } tmp=nxtmap[i][1]; nxtmap[i][1]=nxtmap[i][2]; nxtmap[i][2]=nxtmap[i][3]; nxtmap[i][3]=tmp; nxt=0; for(int j=1; j<T; ++j) for(int k=1; k<T; ++k) if(j!=3 || k!=3) nxt=nxt*10+nxtmap[j][k]; if(!vis[nxt]) { vis[nxt]=true; if(check(nxt)) { printf("%d\n",step+1); return 0; } que.push(rec(nxt,step+1)); } } if(!col[i]) { for(int j=1; j<T; ++j) for(int k=1; k<T; ++k) nxtmap[j][k]=nowmap[j][k]; int tmp=nxtmap[1][i]; nxtmap[1][i]=nxtmap[2][i]; nxtmap[2][i]=nxtmap[3][i]; nxtmap[3][i]=tmp; nxt=0; for(int j=1; j<T; ++j) for(int k=1; k<T; ++k) if(j!=3 || k!=3) nxt=nxt*10+nxtmap[j][k]; if(!vis[nxt]) { vis[nxt]=true; if(check(nxt)) { printf("%d\n",step+1); return 0; } que.push(rec(nxt,step+1)); } tmp=nxtmap[1][i]; nxtmap[1][i]=nxtmap[2][i]; nxtmap[2][i]=nxtmap[3][i]; nxtmap[3][i]=tmp; nxt=0; for(int j=1; j<T; ++j) for(int k=1; k<T; ++k) if(j!=3 || k!=3) nxt=nxt*10+nxtmap[j][k]; if(!vis[nxt]) { vis[nxt]=true; if(check(nxt)) { printf("%d\n",step+1); return 0; } que.push(rec(nxt,step+1)); } } } } return 0; } /* GGGG0 GGGG0 GGGG0 OGOO0 GGGG0 OGOO0 OOOO0 OGGG1 OOOO0 */



