图论乱整理的题
1.P1967 货车运输
题目描述
A 国有 n 座城市,编号从 1 到 n,城市之间有 m 条双向道路。每一条道路对车辆都有重量限制,简称限重。现在有 q 辆货车在运输货物, 司机们想知道每辆车在不超过车辆限重的情况下,最多能运多重的货物。
输入输出格式
输入格式:
输入文件名为 truck.in。
输入文件第一行有两个用一个空格隔开的整数 n,m,表示 A 国有 n 座城市和 m 条道
路。 接下来 m 行每行 3 个整数 x、 y、 z,每两个整数之间用一个空格隔开,表示从 x 号城市到 y 号城市有一条限重为 z 的道路。注意: x 不等于 y,两座城市之间可能有多条道路 。
接下来一行有一个整数 q,表示有 q 辆货车需要运货。
接下来 q 行,每行两个整数 x、y,之间用一个空格隔开,表示一辆货车需要从 x 城市运输货物到 y 城市,注意: x 不等于 y 。
输出格式:
输出文件名为 truck.out。
输出共有 q 行,每行一个整数,表示对于每一辆货车,它的最大载重是多少。如果货
车不能到达目的地,输出-1。
输入输出样例
4 3 1 2 4 2 3 3 3 1 1 3 1 3 1 4 1 3
3 -1 3
说明
对于 30%的数据,0 < n < 1,000,0 < m < 10,000,0 < q< 1,000;
对于 60%的数据,0 < n < 1,000,0 < m < 50,000,0 < q< 1,000;
对于 100%的数据,0 < n < 10,000,0 < m < 50,000,0 < q< 30,000,0 ≤ z ≤ 100,000。
思路:
这个问题叫做『最大瓶颈路径』
最大瓶颈路径一定存在于最大生成树中
反证法:如果最大瓶颈路径不存在与最大生成树中。这些不在最大生成树中的边会和最大生成树形成环。若我们删掉环上最小的边,保留这一条边,会得到一棵新的更大的生成树。这与原来那棵树是最大生成树矛盾了。所以...
注意,最短路不一定在最小生成树上(如一个环的情况)
所以这个题目首先要求最大生成树。
而对于每一个询问,实际上是求树上的两点,路径包括的所有边的权值最小值。
故正解为倍增+LCA
代码:
#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> #define Min(a,b) ((a)<(b)?a:b) #define INF (int)1e9 using namespace std; const int N = 10010; const int M = 50050; const int re = 20; struct Solve { int u,v,w; bool operator < (const Solve &qwq) const { return w > qwq.w; } } t[M]; struct Better { int next,to,w; } e[N<<1]; int n,m,q; int vis[N],dad[N],dep[N],jumps[N][re+1],j[N][re+1]; void Swap(int &a,int &b) { int tmp=a; a=b,b=tmp; } int top,head[N]; void add(int u,int v,int w) { top++; e[top].next=head[u]; head[u]=top; e[top].to=v; e[top].w=w; } void dfs(int u) { vis[u]=1; for(int i=1; i<=re; ++i) jumps[u][i]=jumps[jumps[u][i-1]][i-1], j[u][i]=Min(j[u][i-1],j[jumps[u][i-1]][i-1]); for(int i=head[u]; i; i=e[i].next) { int v=e[i].to; if(!vis[v]) { dep[v]=dep[u]+1; jumps[v][0]=u; j[v][0]=e[i].w; dfs(v); } } } int getdad(int x) { return x == dad[x] ? x : dad[x]=getdad(dad[x]); } int getlca(int a,int b) { if(dep[a]<dep[b]) Swap(a,b); for(int i=re; i>=0; --i) if(dep[jumps[a][i]]>=dep[b]) a=jumps[a][i]; if(a==b) return a; for(int i=re; i>=0; --i) if(jumps[a][i]!=jumps[b][i]) a=jumps[a][i],b=jumps[b][i]; return jumps[a][0]; } int ask(int x,int f) { int ret=INF; int deep=dep[x]-dep[f]; for(int i=0; i<=re; ++i) if(deep & (1<<i))///若能跳 ret=Min(ret,j[x][i]),x=jumps[x][i]; return ret; } int main() { memset(j,0x3f,sizeof(j)); scanf("%d%d",&n,&m); for(int i=1; i<=m; ++i) scanf("%d%d%d",&t[i].u,&t[i].v,&t[i].w); sort(t+1,t+1+m); for(int i=1; i<=n; ++i) dad[i]=i; for(int i=1; i<=m; ++i) { int die1=getdad(t[i].u); int die2=getdad(t[i].v); if(die1!=die2) { dad[die1]=die2; add(t[i].u,t[i].v,t[i].w); add(t[i].v,t[i].u,t[i].w); } } for(int i=1; i<=n; ++i) if(!vis[i]) dfs(i); scanf("%d",&q); for(int i=1,x,y; i<=q; ++i) { scanf("%d%d",&x,&y); if(getdad(x)!=getdad(y)) { printf("-1\n"); continue; } int lca=getlca(x,y); printf("%d\n",Min(ask(x,lca),ask(y,lca))); } return 0; }
2.P1073 最优贸易
题目描述
C 国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市。任意两个
城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路,一部分
为双向通行的道路,双向通行的道路在统计条数时也计为 1 条。
C 国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价
格不一定相同。但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息
之后,便决定在旅游的同时,利用商品在不同城市中的差价赚回一点旅费。设 C 国 n 个城
市的标号从 1~ n,阿龙决定从 1 号城市出发,并最终在 n 号城市结束自己的旅行。在旅游的
过程中,任何城市可以重复经过多次,但不要求经过所有 n 个城市。阿龙通过这样的贸易方
式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品――水晶球,并在之后经过的另
一个城市卖出这个水晶球,用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游,他决定
这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。
假设 C 国有 5 个大城市,城市的编号和道路连接情况如下图,单向箭头表示这条道路
为单向通行,双向箭头表示这条道路为双向通行。
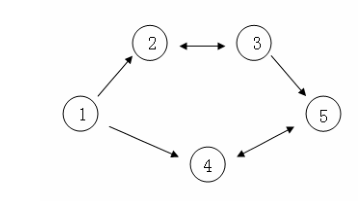
假设 1~n 号城市的水晶球价格分别为 4,3,5,6,1。
阿龙可以选择如下一条线路:1->2->3->5,并在 2 号城市以 3 的价格买入水晶球,在 3
号城市以 5 的价格卖出水晶球,赚取的旅费数为 2。
阿龙也可以选择如下一条线路 1->4->5->4->5,并在第 1 次到达 5 号城市时以 1 的价格
买入水晶球,在第 2 次到达 4 号城市时以 6 的价格卖出水晶球,赚取的旅费数为 5。
现在给出 n 个城市的水晶球价格,m 条道路的信息(每条道路所连接的两个城市的编号
以及该条道路的通行情况)。请你告诉阿龙,他最多能赚取多少旅费。
输入输出格式
输入格式:
第一行包含 2 个正整数 n 和 m,中间用一个空格隔开,分别表示城市的数目和道路的
数目。
第二行 n 个正整数,每两个整数之间用一个空格隔开,按标号顺序分别表示这 n 个城
市的商品价格。
接下来 m 行,每行有 3 个正整数,x,y,z,每两个整数之间用一个空格隔开。如果 z=1,
表示这条道路是城市 x 到城市 y 之间的单向道路;如果 z=2,表示这条道路为城市 x 和城市
y 之间的双向道路。
输出格式:
输出文件 trade.out 共 1 行,包含 1 个整数,表示最多能赚取的旅费。如果没有进行贸易,
则输出 0。
输入输出样例
5 5 4 3 5 6 1 1 2 1 1 4 1 2 3 2 3 5 1 4 5 2
5
说明
【数据范围】
输入数据保证 1 号城市可以到达 n 号城市。
对于 10%的数据,1≤n≤6。
对于 30%的数据,1≤n≤100。
对于 50%的数据,不存在一条旅游路线,可以从一个城市出发,再回到这个城市。
对于 100%的数据,1≤n≤100000,1≤m≤500000,1≤x,y≤n,1≤z≤2,1≤各城市
水晶球价格≤100。
NOIP 2009 提高组 第三题
思路:
大概的思路就是寻找在i点之前的水晶球中价值最小的与i点之后水晶球中价值最大的价值之差
所以我们搞两遍spfa(一遍正序,一遍逆序)
正序找最小,逆序找最大
代码:
#include <iostream> #include <cstring> #include <cstdio> #include <queue> #include <cmath> using namespace std; const int Maxn = 100001; const int Maxm = 500001; struct road1 { int next,to; }e1[Maxm],e2[Maxm]; struct road2 { int head; }h1[Maxn],h2[Maxn]; int top1,top2; int n,m; ///输入数据(水晶球价值) int a[Maxn]; ///(卖出)maxx数组存放正序时该点之后能够到达的点中最大的点的水晶球的价值 ///(买入)minn数组则存放正序时该点之前的水请求的最大价值 int minn[Maxn],maxx[Maxn]; bool vis[Maxn]; void add1(int u,int v) {///正向建边 top1++; e1[top1].to=v; e1[top1].next=h1[u].head; h1[u].head=top1; } void add2(int u,int v) {///逆向建边 top2++; e2[top2].to=v; e2[top2].next=h2[u].head; h2[u].head=top2; } inline int min3(int x,int y,int z) { if(x<y && x<z) return x; if(y<x && y<z) return y; return z; } inline int max3(int x,int y,int z) { if(x>y && x>z) return x; if(y>x && y>z) return y; return z; } void getmin() { memset(minn,0x7f7f,sizeof(minn)); queue<int>q; ///正序时 1 是起点 q.push(1); minn[1]=a[1]; while(!q.empty()) { int u=q.front(); q.pop(); for(int i=h1[u].head; i; i=e1[i].next) { int v=e1[i].to; minn[v]=min3(minn[u],minn[v],a[v]); if(!vis[v]) { q.push(v); vis[v]=true; } } } } void getmax() { memset(vis,false,sizeof(vis)); queue<int>q; ///逆序寻找 q.push(n); maxx[n]=a[n]; while(!q.empty()) { int u=q.front(); q.pop(); for(int i=h2[u].head; i; i=e2[i].next) { int v=e2[i].to; maxx[v]=max3(minn[u],minn[v],a[v]); if(!vis[v]) { q.push(v); vis[v]=true; } } } } int main() { scanf("%d%d",&n,&m); for(int i=1; i<=n; ++i) scanf("%d",&a[i]); for(int i=1,x,y,z; i<=m; ++i) { scanf("%d%d%d",&x,&y,&z); add1(x,y),add2(y,x); if(z!=1) add1(y,x),add2(x,y); } getmin(); getmax(); int ans=0; ///ans只需要在逆向建边中找到的本为 for(int i=1; i<=n; ++i) ans=max(ans,maxx[i]-minn[i]); printf("%d\n",ans); return 0; }
3.[USACO09OCT]热浪Heat Wave
题目描述
The good folks in Texas are having a heatwave this summer. Their Texas Longhorn cows make for good eating but are not so adept at creating creamy delicious dairy products. Farmer John is leading the charge to deliver plenty of ice cold nutritious milk to Texas so the Texans will not suffer the heat too much.
FJ has studied the routes that can be used to move milk from Wisconsin to Texas. These routes have a total of T (1 <= T <= 2,500) towns conveniently numbered 1..T along the way (including the starting and ending towns). Each town (except the source and destination towns) is connected to at least two other towns by bidirectional roads that have some cost of traversal (owing to gasoline consumption, tolls, etc.). Consider this map of seven towns; town 5 is the
source of the milk and town 4 is its destination (bracketed integers represent costs to traverse the route):
[1]----1---[3]-
/ \
[3]---6---[4]---3--[3]--4
/ / /|
5 --[3]-- --[2]- |
\ / / |
[5]---7---[2]--2---[3]---
| /
[1]------Traversing 5-6-3-4 requires spending 3 (5->6) + 4 (6->3) + 3 (3->4) = 10 total expenses.
Given a map of all the C (1 <= C <= 6,200) connections (described as two endpoints R1i and R2i (1 <= R1i <= T; 1 <= R2i <= T) and costs (1 <= Ci <= 1,000), find the smallest total expense to traverse from the starting town Ts (1 <= Ts <= T) to the destination town Te (1 <= Te <= T).
德克萨斯纯朴的民眾们这个夏天正在遭受巨大的热浪!!!他们的德克萨斯长角牛吃起来不错,可是他们并不是很擅长生產富含奶油的乳製品。Farmer John此时以先天下之忧而忧,后天下之乐而乐的精神,身先士卒地承担起向德克萨斯运送大量的营养冰凉的牛奶的重任,以减轻德克萨斯人忍受酷暑的痛苦。
FJ已经研究过可以把牛奶从威斯康星运送到德克萨斯州的路线。这些路线包括起始点和终点先一共经过T (1 <= T <= 2,500)个城镇,方便地标号為1到T。除了起点和终点外地每个城镇由两条双向道路连向至少两个其它地城镇。每条道路有一个通过费用(包括油费,过路费等等)。
给定一个地图,包含C (1 <= C <= 6,200)条直接连接2个城镇的道路。每条道路由道路的起点Rs,终点Re (1 <= Rs <= T; 1 <= Re <= T),和花费(1 <= Ci <= 1,000)组成。求从起始的城镇Ts (1 <= Ts <= T)到终点的城镇Te(1 <= Te <= T)最小的总费用。
输入输出格式
输入格式:
第一行: 4个由空格隔开的整数: T, C, Ts, Te
第2到第C+1行: 第i+1行描述第i条道路。有3个由空格隔开的整数: Rs, Re和Ci
输出格式:
一个单独的整数表示从Ts到Te的最小总费用。数据保证至少存在一条道路。
输入输出样例
7 11 5 4 2 4 2 1 4 3 7 2 2 3 4 3 5 7 5 7 3 3 6 1 1 6 3 4 2 4 3 5 6 3 7 2 1
7
说明
【样例说明】
5->6->1->4 (3 + 1 + 3)
思路:
裸的最短路问题。。
1)floyd->60
2)SPFA->AC
代码:
1)floyd

//60 #include <iostream> #include <cstdio> #include <cstring> using namespace std; const int T = 2501; int n,m,op,ed; int map[T][T]; int main() { scanf("%d%d%d%d",&n,&m,&op,&ed); memset(map,0x3f,sizeof(map)); for(int i=1; i<=n; i++) map[i][i]=0; for(int i=1,u,v,w; i<=m; i++) { scanf("%d%d%d",&u,&v,&w); map[u][v]=map[v][u]=w; } for(int k=1; k<=n; k++) for(int i=1; i<=n; i++) for(int j=1; j<=n; j++) map[i][j]=min(map[i][j],map[i][k]+map[k][j]); printf("%d",map[op][ed]); return 0; }
2)SPFA

#include <iostream> #include <cstdio> #include <cstring> #include <queue> using namespace std; const int N = 2501; const int M = 6201; int n,m,op,ed; queue <int> q; struct node { int next,to,w; }e[M<<1]; int top,head[N]; void add(int u,int v,int w) { top++; e[top].to=v; e[top].w=w; e[top].next=head[u]; head[u]=top; } int dis[N]; bool vis[N]; void spfa() { memset(dis,0x3f,sizeof(dis)); dis[op]=0; vis[op]=true; int u,v; q.push(op); while(!q.empty()) { u=q.front(); q.pop(); for(int i=head[u]; i; i=e[i].next) { v=e[i].to; if(dis[u]+e[i].w<dis[v]) { dis[v]=dis[u]+e[i].w; if(!vis[v]) { vis[v]=true; q.push(v); } } } vis[u]=false; } } int main() { scanf("%d%d%d%d",&n,&m,&op,&ed); for(int i=1,u,v,w; i<=m; i++) { scanf("%d%d%d",&u,&v,&w); add(u,v,w),add(v,u,w); } spfa(); printf("%d",dis[ed]); return 0; }



