日照学习提高班day4测试
A

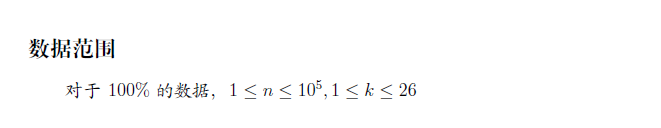
思路:
一看到这个题,他不仅要求输出字典序最小的串,还要满足两两不重复,所以我们可以先输出ababab...什么的,最后缀上要求的k-2种字母
坑点:
当然这样想是不完全的!该题是拥有许多特殊情况的!
例:
①当n==k的时候(直接从字符‘a’往后面一个一个接着输出就好啦~)
②除去①之后若k==1(即只允许一中字符出现,但是又需要输出多个字符的情况)(直接输出-1)
③当k>n的时候(直接输出-1)
④当k==2的时候(能输出多少对ab就输出几对ab,若不成对的话,倒数第二个输出a,即abababababababa什么的)
⑤当k==3的时候(最后输出‘c’,前面能输出几对ab就输出几对ab,若不成对的话,倒数第二个输出a,即abababababababa什么的)
⑥其余为普通情况(见思路)
上代码:
#include <iostream> #include <cstdio> using namespace std; const int Maxn = 10010; int n,k,cnt; int p,p2; //p是ab在不特殊情况下的总个数 //p2是在不特殊情况下除ab以外的总个数 int main() { freopen("str.in","r",stdin); freopen("str.out","w",stdout); scanf("%d%d",&n,&k); if(n==k) { for(int i=0;i<n;++i) printf("%c",(char)i+'a'); return 0; } if(k==1 || k>n) { printf("-1"); return 0; } p=n-k+2,p2=k-2; bool flag=false; if(k<=2) { while(cnt<n) { if(flag) printf("b"),flag=false; else printf("a"),flag=true; ++cnt; } return 0; } if(k==3) { while(cnt<n-1) { if(flag) printf("b"),flag=false; else printf("a"),flag=true; ++cnt; } printf("c"); return 0; } while(cnt<p) { if(flag) printf("b"),flag=false; else printf("a"),flag=true; ++cnt; } for(int i=3;i<3+p2;++i) printf("%c",(char)i+96); return 0; }
B



思路:
①这是一道数论题,只需要根据排列组合推出来数学公式,然后用快速幂搞一搞即可(因为范围很大嘛~)
②在前k个点方案数的寻找中,也可以使用搜索
公式:
ans=ksm(k,k-1)%Mod * ksm(n-k,n-k)%Mod;
坑点:
一、我怎么知道这个公式啊啊啊!!!
所以需要手动推导一下!!!
①ksm(k,k-1)
- k==1的时候
- 只有一种情况:1 —> 1
- k==2的时候
- 只有2种情况:1 —> 2 ,2 —> 1
- k==3的时候
- 情况稍微多一点: 我们这里用一个表格来进行演示!
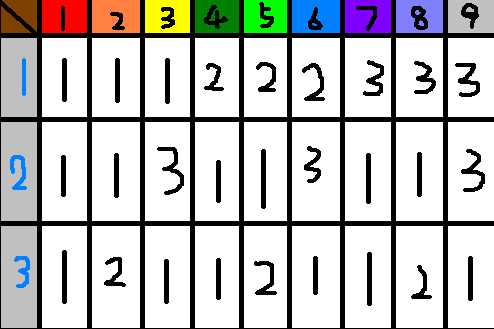
- 若还不懂,请自己手动实现一下吧还是。。。
②ksm(n-k,n-k)
- 因为题目中提到除那k个点之外,其他点不能够连到1,而又因为k个点每个点都必须能够走到1,这即是说明后n-k个点不能够连到k个点,所以他们能够胡乱连,只要不到k个点即可,
- 所以方案数为ksm(n-k,n-k);
- (因为每个点都有n-k种选择)
③至于为什么要%Mod
- 对此我只能说:题目要求。。。。
二、在搜索的时候数组一定不要开到8就算了,会T掉....
所以要开到9!!
看似数据中存在k==9的情况qwq ,因为我开到8后T了3个点,但是多加了一个之后就A了。。。
上代码:
- 数论版:
#include <iostream> #include <cstdio> #define LL long long using namespace std; const int Mod = 1e9 + 7; LL n,k,ans; inline LL read(LL &AC) { char ch=' ';LL x=0,f=1; for(; (ch!='-') && ((ch<'0')||(ch>'9')); ch=getchar()); if(ch=='-') f=-1,ch=getchar(); for(; ch>='0' && ch<='9'; ch=getchar()) x=x*10+ch-48; AC=x*f; return AC; } inline LL ksm(LL a,LL p) { LL ret = 1; a%=Mod; for(; p; p>>=1, a=a*a%Mod) if(p&1) ret=ret*a%Mod; return ret; } int main() { read(n),read(k); ans=ksm(k,k-1)%Mod*ksm(n-k,n-k)%Mod; printf("%lld",ans); return 0; }
- 搜索版:
#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> #define LL long long using namespace std; const int Mod = 1e9 + 7; const int Maxk = 10; LL n,k,ans; int pi[Maxk]; inline LL read(LL &AC) { char ch=' ';LL x=0,f=1; for(; (ch!='-') && ((ch<'0')||(ch>'9')); ch=getchar()); if(ch=='-') f=-1,ch=getchar(); for(; ch>='0' && ch<='9'; ch=getchar()) x=x*10+ch-48; AC=x*f; return AC; } inline LL ksm(LL a,LL p) { LL ret = 1; a%=Mod; for(; p; p>>=1, a=a*a%Mod) if(p&1) ret=ret*a%Mod; return ret; } inline bool check() { bool vis[Maxk]; memset(vis,false,sizeof(vis)); int now=1; while(!vis[now]) { vis[now]=true; now=pi[now]; } ///从 1 出发必须能够回到 1 if(now!=1) return false; for(int i=1; i<=k; ++i) { if(!vis[i]) { bool vis2[Maxk]; memset(vis2,false,sizeof(vis2)); int now2=i; while(!vis2[now2] && !vis[now2]) { vis2[now2]=true; now2=pi[now2]; } if(!vis[now2]) return false; } } return true; } void dfs(int now) { if(now==k+1) { if(check()) ans++; return ; } for(int i=1; i<=k; ++i) { pi[now]=i; dfs(now+1); } } int main() { read(n),read(k); dfs(1); ans=ans*ksm(n-k,n-k)%Mod; printf("%lld",ans); return 0; }
C



思路:
这题需要优化的dp!!!
但是为什么可以优化那?
首先时间上的优化:
因为每一次递推改变的是一个范围内的值,所以能用差值维护。
其次空间上的优化:
每一步仅与他的上一步有关,能用滚动数组。
坑点:
最后ans记录的时候用的是last,不是now,因为最后有一次互换操作!
上代码:
#include <iostream> #include <cstdlib> #include <cstdio> #include <cmath> #define LL long long using namespace std; const int Maxn = 5001; const int Mod = 1e9 + 7; int n,a,b,k; ///滚动数组 ,二维是代表终点在第几层 LL dp[2][Maxn]; ///up代表第i层能走到的最上方的层数为...,down反之 int up[Maxn],down[Maxn]; int main() { freopen("lift.in","r",stdin); freopen("lift.out","w",stdout); scanf("%d%d%d%d",&n,&a,&b,&k); int last=0,now=1; ///初始化:自己从a出发到a的方法只有1种 dp[last][a]=1; for(int i=1; i<=n; ++i) { ///处理每一层到达b的距离 int dis=abs(i-b); /* 1-n是从上到下,所以i-dis+1要比i+dis-1要小,所以i-dis+1在上方 见图示 又因为i可能减不了,但是up又不能够<1,所以在i-dis+1跟1中取max down同理 */ up[i]=max(1,i-dis+1); down[i]=min(n,i+dis-1); } for(int i=1; i<=k; ++i) { ///使用滚动数组要先将将要更新的清零 for(int j=1; j<=n; ++j) dp[now][j]=0; for(int j=1; j<=n; ++j) { (dp[now][up[j]]+=dp[last][j])%Mod; (dp[now][down[j]+1]-=dp[last][j])%Mod; } ///处理前缀和 for(int j=1; j<=n; ++j) (dp[now][j]+=dp[now][j-1])%Mod; ///滚动数组(处理完前缀和之后,上一个就已经没用了,减去) for(int j=1; j<=n; ++j) (dp[now][j]-=dp[last][j])%Mod; ///进行交换 swap(last,now); } int ans=0; /* 为什么用last不用now呢? 因为上一个for循环中最后结束的时候又把last跟now换了 所以本来最后i==k时now代表k,换完之后变为last */ ///因为每一层都有可能是终点,ans都累加一遍即可 for(int i=1; i<=n; ++i) (ans+=dp[last][i])%Mod; ///防止出现负数 ans=(ans+Mod)%Mod; cout<<ans; return 0; }



