7-7 列出连通集

给定一个有N个顶点和E条边的无向图，请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时，假设我们总是从编号最小的顶点出发，

按编号递增的顺序访问邻接点。

输入格式:

输入第1行给出2个整数N(0<N≤10)和E，分别是图的顶点数和边数。随后E行，每行给出一条边的两个端点。每行中的数字之间用1空格分隔。

输出格式:

按照"{ v1​ v2​ ... vk​ }"的格式，每行输出一个连通集。先输出DFS的结果，再输出BFS的结果。

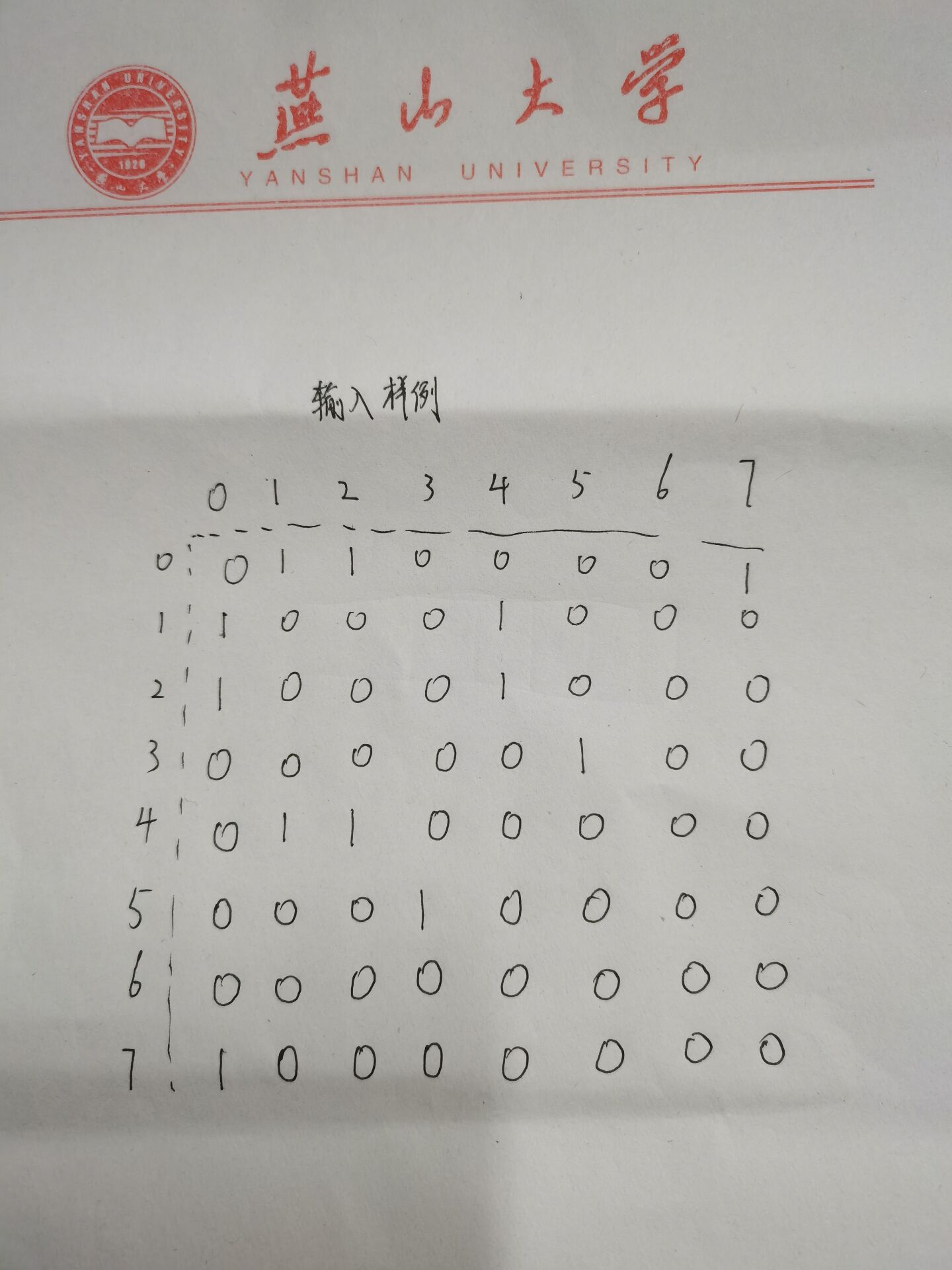
输入样例:

8 6
0 7
0 1
2 0
4 1
2 4
3 5

 

结尾无空行

输出样例:

{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }
思路：
1.首先确认图的存储方式，由于N(0<N≤10)，需要的内存较少，采用邻接矩阵的方式来存储图
2.DFS需要使用递归遍历，而BFS需要使用队列，在这里使用数组模拟队列
3.没有边的顶点单独输出

 

 代码：

void dfs(int i,int Nv)
{
    cout<<i<<" ";
    visited[i]=1;//将访问过的顶点沉默
    for(int j=0;j<Nv;j++)
    {
        if(visited[j]==0&&a[i][j]==1)//如果顶点j没有被访问过且i和j之间有边 
        {
            dfs(j,Nv);//进行递归
        }
    }
}

void dfstraversal(int Nv)
{
    for(int i=0;i<Nv;i++)
    {
        visited[i]=0;//初始化为0
    }
    for(int i=0;i<Nv;i++)
    {
//这里的代码是因为需要分开输出联通块，进行一次for循环，仔细理解一下
//dfs的特性就是每次都可以将一个连通块全部走完
        if(!visited[i])//如果没有被访问过
        {
　　
            cout<<"{ ";
            dfs(i,Nv);
            cout<<"}"<<endl;
        }
    }
}

void bfs(int nv)
{
    int l=0,r=0;
    int queue[1000];//用数组模拟队列，l为队头，r为队尾
    for(int i=0;i<nv;i++)
    {
        visited[i]=0;
    }
    for(int i=0;i<nv;i++)
    {
        if(!visited[i])
        {
            cout<<"{ ";
            queue[r++]=i;
            visited[i]=1;
            while(l!=r)//当队列不为空时
            {
                int tmp=queue[l++];
                cout<<tmp<<" ";
                for(int j=0;j<nv;j++)
                {
                    if(a[tmp][j]&&!visited[j])
                    {
                        visited[j]=1;
                        queue[r++]=j;
                    }
                }
            }
            cout<<"}"<<endl;
        }
    }
}

解释一下：
刚开始l和r都指向下标为0的地方，先将元素0入队，r++，来到下标为1的地方，然后用tmp将0取出，l++，并用一层for循环寻找出所有与0连接的元素，全部入队
for循环结束后，回到while循环，直到将第一个联通块输出完。

 

 

完整代码：
#include<iostream>
using namespace std;
#define max 10
int visited[max];
int a[max][max];
void dfs(int i,int Nv)
{
    cout<<i<<" ";
    visited[i]=1;
    for(int j=0;j<Nv;j++)
    {
        if(visited[j]==0&&a[i][j]==1) 
        {
            dfs(j,Nv);
        }
    }
}
void dfstraversal(int Nv)
{
    for(int i=0;i<Nv;i++)
    {
        visited[i]=0;
    }
    for(int i=0;i<Nv;i++)
    {
        if(!visited[i])
        {
            cout<<"{ ";
            dfs(i,Nv);
            cout<<"}"<<endl;
        }
    }
}
void bfs(int nv)
{
    int l=0,r=0;
    int queue[1000];
    for(int i=0;i<nv;i++)
    {
        visited[i]=0;
    }
    for(int i=0;i<nv;i++)
    {
        if(!visited[i])
        {
            cout<<"{ ";
            queue[r++]=i;
            visited[i]=1;
            while(l!=r)
            {
                int tmp=queue[l++];
                cout<<tmp<<" ";
                for(int j=0;j<nv;j++)
                {
                    if(a[tmp][j]&&!visited[j])
                    {
                        visited[j]=1;
                        queue[r++]=j;
                    }
                }
            }
            cout<<"}"<<endl;
        }
    }
}
int main()
{
    int N,E;
    cin>>N>>E;
    int v1,v2;
    for(int i=0;i<E;i++)
    {
        cin>>v1>>v2;
        a[v1][v2]=a[v2][v1]=1;
    }
    dfstraversal(N);
    bfs(N);
    return 0;
}

 加油，陌生人！