浮点数如何表示，以及为什么会出现精度问题

浮点数在计算机中也是用二进制表示的，只不过有一定规则（公式）

 

 

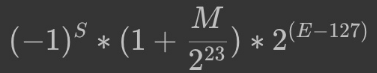
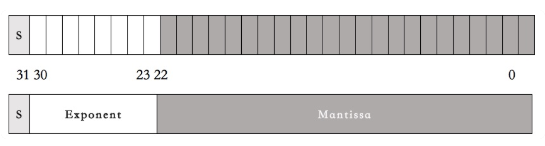
 第一段占 1bit，表示符号位。代称为 S（sign）。

第二段占 8bits，表示指数。代称为 E（Exponent）。

第三段占 23bits，表示尾数。代称为 M（Mantissa）。

 

 

 

对 3.14 这个小数进行表示
是正数。所以，S = 0
2^1 < 3.14 <2^2。所以，n=1， n+127 = 128。所以，E=128。
(3.14 - 2) / (4 - 2) = 0.57， 而 0.57*2^{23} = 4781506.56，四舍五入，得到 M = 4781507。因为有四舍五入，所以，产生了浮点数据的精度问题。
至此，根据小数3.14以及上面的公式算出了S E M

把 S、E、M 转成二进制，放入二进制位的三段得到 3.14 的二进制表示

 

 

 为什么会产生精度问题？

产生精度问题，其实是将二进制的3段变量重新带入公式，算出的结果与原值不同的问题

问题就出在，第一次计算M时就有了精度问题4781506.56四舍五入4781507