实验3

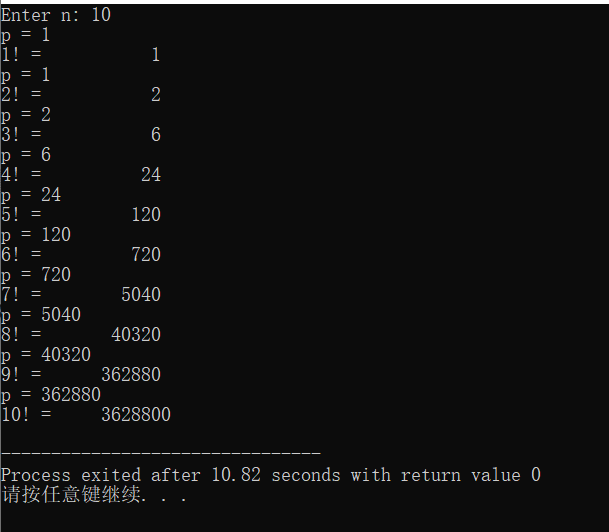
#include <stdio.h>
long long fac(int n);

int main()
{
    int i,n;
    
    printf("Enter n: ");
    scanf("%d", &n);
    
    for(i = 1;i <= n; ++i)
       printf("%d! = %11d\n", i, fac(i));
       
    return 0;
}

long long fac(int n)
{
    static long long p = 1;
    
    
    
    p = p * n;
    
    return p;
}

#include <stdio.h>
int func(int , int);

int main()
{
    int k = 4, m = 1, p1, p2;
    
    
    p1 = func(k, m);
    p2 = func(k, m);
    printf("%d%d\n", p1, p2);
    
    return 0;
}

int func(int a, int b)
{
    static int m = 0, i = 2;
    
    i += m + 1;
    m = i + a + b;
    
    return (m); 
}

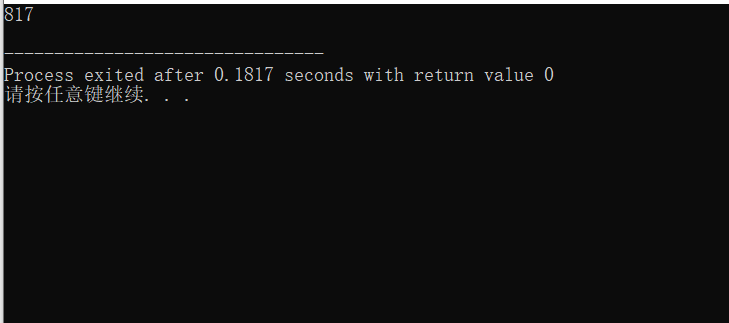
 运行结果与我理论分析一致。 static变量的特性就是在一次调用之后赋给某一变量的值保持不变并可以被继续调用。

迭代

#include <stdio.h>

void printsymbol(int n , char symbol);

int main()
{
    int n;
    char symbol;
    
    while( scanf("%d %c", &n, &symbol) != EOF)
    {
        printsymbol(n, symbol);
        printf("\n");
        
    }
    
    return 0;
}

void printsymbol(int n, char symbol)
{
    int i;
    for(i = 1;i <= n; i++)
    printf("%c", symbol);
}

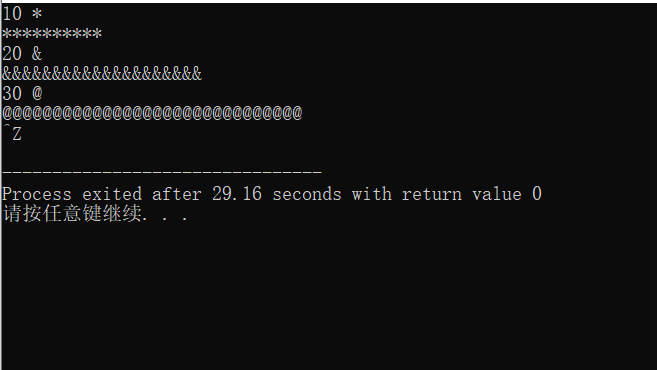
递归

#include <stdio.h>

void printsymbol(int n , char symbol);

int main()
{
    int n;
    char symbol;
    
    while( scanf("%d %c", &n, &symbol) != EOF)
    {
        printsymbol(n, symbol);
        printf("\n");
        
    }
    
    return 0;
}

void printsymbol(int n, char symbol)
{
    if(n == 1)
    printf("%c", symbol);
    else
    {
    printsymbol(n-1, symbol);
    printf("%c", symbol);
    }
}

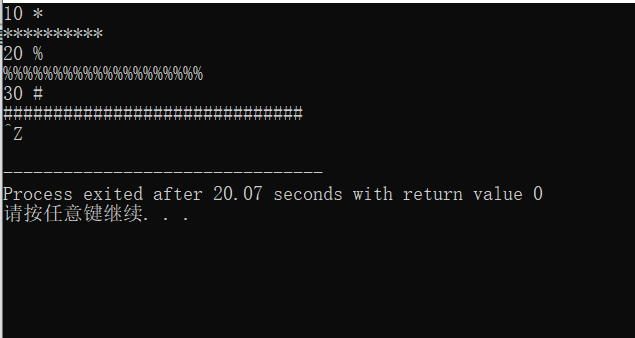
我认为递归的实现方式更好，因为这种实现方式在思维上可以偷懒，只要将最基本的抽离出来再进行函数的嵌套使用即可。

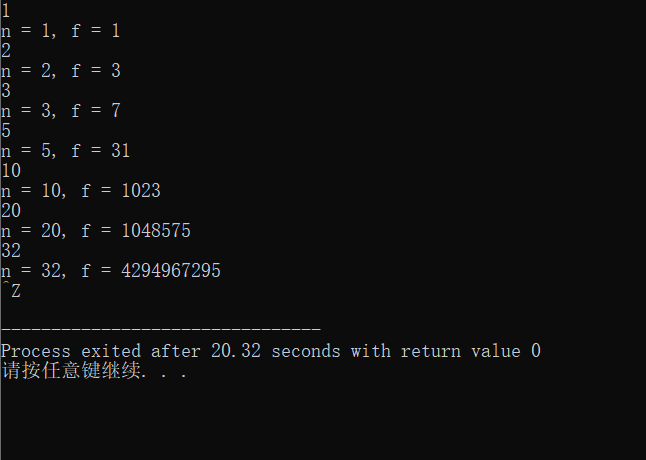
#include  <stdio.h>
long long fun(int n);

int main()
{
    int n;
    long long f;
    
    while ( scanf("%d", &n) != EOF)
    {
        f = fun(n);
        printf("n = %d, f = %lld\n", n , f);
    }
    
    return 0;
 } 
 
 long long fun(int n)
 {
     long long t;
     if (n == 0)
     return 0;
    else if (n == 1)
    {
        return 1;
    }
    else
    {
    t = 2 * fun(n-1) + 1;
    return t;
    }
     
 }

#include <stdio.h>
#include <math.h>
int isPrime(int );
int main()
{
    int x, t;
    for(x = 101, t = 0; x <= 200; x++)
    if(isPrime(x) == 0)
    {
        printf("%4d", x);
        t++;
    }
    printf("\n101~200之间一共有%d个非素数", t);
    return 0;
}

int isPrime( int n)
{
    int i;
    for(i=2;i<=sqrt(n); i++)
    if(n%i == 0)
     return 0;
    else if (i > sqrt(n))
    {
        return 1;
    }
}

 

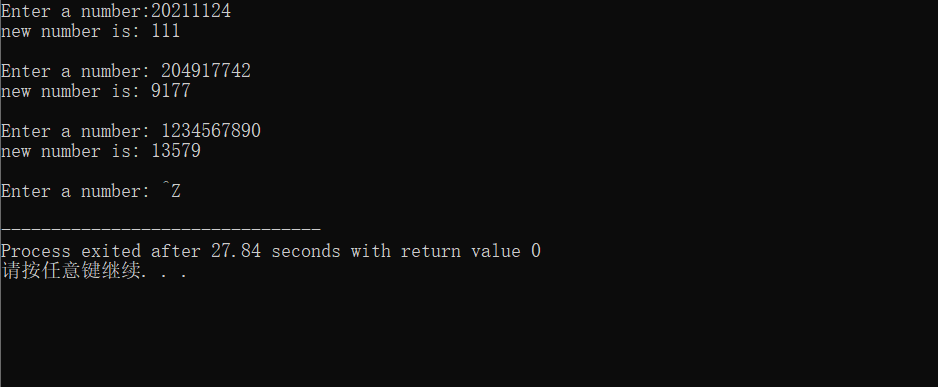
#include<stdio.h>
long fun(long s);

int main()
{
    long s,t;
    
    printf("Enter a number:");
    while (scanf("%ld",&s)!=EOF)
    {
        t = fun(s);
        printf("new number is: %ld\n\n",t);
        printf("Enter a number: ");
    }
    return 0;
}
long fun(long s)
{
    long int p;
    int m=0 , n=1;
    while(s > 0)
        {
        p = s%10;
        if(p%2 != 0)
       {
           m = m + n*p;
        n = n * 10;
        } 
        s = s/10;
        }
    return m;
}

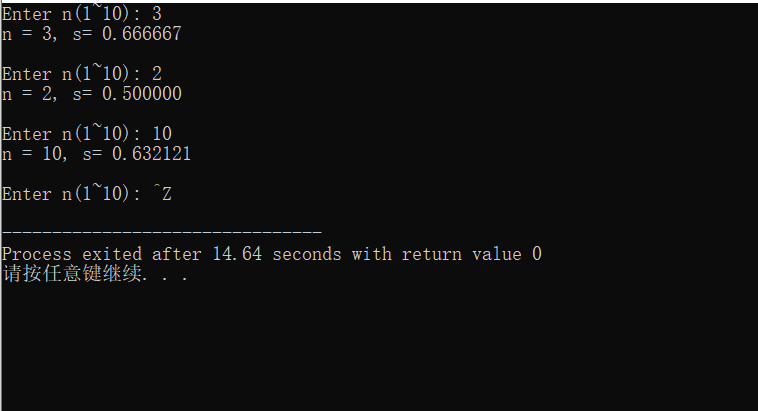
#include <stdio.h>
double fun(int n); 

int main()
{
    int n;
    double s;
    
    printf("Enter n(1~10): ");
    while (scanf("%d", &n) != EOF)
   {
    s = fun(n); 
    printf("n = %d, s= %f\n\n", n, s);
    printf("Enter n(1~10): ");
   }
    return 0;
}
double fun(int n)
{
    double t=1, j;
    int  m=1, i, sign=-1;
    if(n == 1)
    return 1;
    else
    {
        for(i=2;i<=n;i++)
    {
        m = m * i;
        j = sign *(float)1/m;
        t = t + j;
        sign = -sign;
    }
        return t;
    }
}

 本次实验巩固了第四章函数的相关知识，将书本上的理论知识运用在了实践中，同时对于一些问题的函数抽象能力仍有待提高。