强盗团伙（啊哈-并查集[模板]）

题目

快过年了，犯罪分子们也开始为年终奖“奋斗”了，小哼的家乡出现了多次抢劫事件。由于强盗人数过于庞大，作案频繁，警方想查清楚到底有几个犯罪团伙实在是太不容易了，不过警察叔叔还是搜集到了一些线索，需要咱们帮忙分析一下。

给定n个强盗和m调线索，输出有多少个犯罪团伙。

输入

第一行两个数n和m分别表示强盗人数和m条线索
接下来m，每行两个数x和y,表示x和y是同伙。

输出

输出一个数，表示犯罪团伙的个数。

输入示例

11 10
1 2
3 4
5 2
4 6
2 6
7 11
8 7
9 7
9 11
1 6

输出示例

3

其他说明

1<=n,m<=1000.

 

分析

这道题是一道简单的并查集模板题（不会并查集看https://www.cnblogs.com/zxjhaha/p/11207928.html）。初始化n个集合，使每个人的祖宗成为本身。若两个强盗是团伙，则将它们所在的集合合并。最后判断有几个元素祖先是其本身即可。

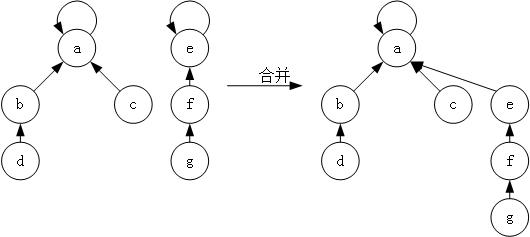
代码

#include <bits/stdc++.h>
using namespace std;
int n,m,fa[1005];
struct bcj //表示两个强盗是团伙 
{
	int x1,y1;
}a[1005];
void init() //初始化
{
	for(int i=1;i<=n;i++) fa[i]=i;
}
int findf(int x) //寻找一个点的祖先 
{
	if(fa[x]==x) return x;
	return fa[x]=findf(fa[x]); //路径压缩
}
void unionn(int x,int y) //合并 
{
	fa[findf(x)]=findf(y);
}
bool isf(int x,int y) //判断两个点的祖先是否一致 
{
	if(findf(x)==findf(y)) return 1;
	return 0;
}
int main()
{
	cin>>n>>m;
	init();
	for(int i=0;i<m;i++)
	{
		cin>>a[i].x1>>a[i].y1;
		unionn(a[i].x1,a[i].y1); //合并 
	}
	int cnt=0; //cnt为计数器 
	for(int i=1;i<=n;i++)
	{
		//cout<<fa[i]<<" "<<i<<endl;
		if(fa[i]==i) cnt++; //判断一个点的祖先是不是它本身，若是计数器++ 
	}
	cout<<cnt;
	return 0;
}