20175221 《信息安全系统设计基础》第4周学习总结

教材学习内容总结

1. 进制转换

2. 三种运算

3. 信息=位+上下文

4. 数值运算

5. 信息的存储

教材学习中的问题和解决过程

实验楼教材导读与每周考试重点：

• 问题1：教材2.6运行程序未找到匹配序列

• 问题1解决方案：按照教材题目要求，编写代码输出一个整数与其浮点数的十六进制

• 
• 但是当我寻找二者二进制的匹配序列时，并未找到。百度了好久，发现是“大端小端”问题，回头翻阅教材2.5的内容。编写程序查看地址首位的数字来判断我的电脑是大端还是小端
• 

 

• 于是就解释得通了，小端数字需颠倒来读取，同时也知常见的windows、Linux系统都是小端模式，网络传输则是大端模式（参考【编程基础】简单理解大小端那些事儿）

• 

• 将输出的十六进制重新排序并匹配二进制数字
  
         0   0   3   5   9   1   4   1
      0000 0000 0011 0101 1001 0001 0100 0001
                 
           4   A   5   6   4   5   0   4
        0100 1010 0101 0110 0100 0101 0000 0100
  
  

   

• 可看出21位匹配，开头末尾不匹配。为了验证是大端小端的问题导致一开始理解错误，我再次选了教材上的12345做实验，结果正确
• 

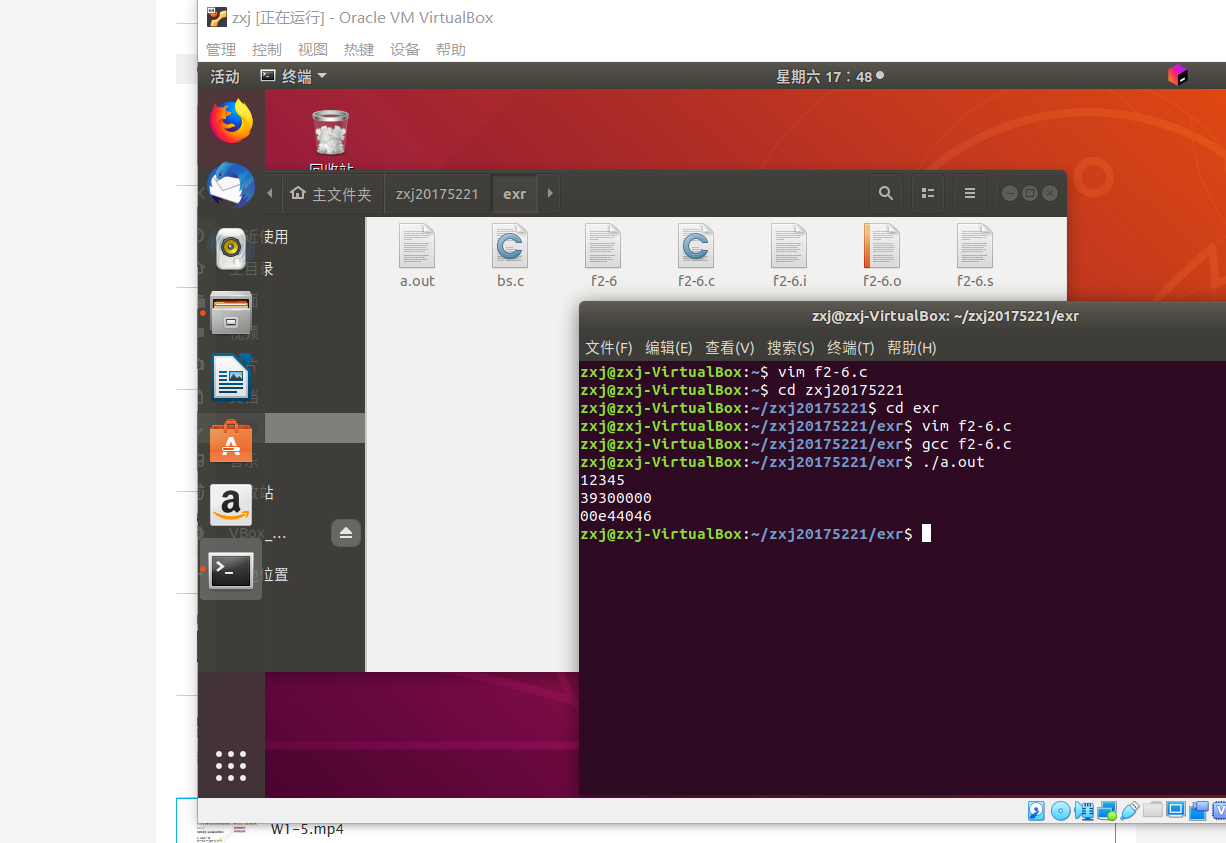
• 可看出13位匹配
   
        0   0   0   0   3   0   3   9
      0000 0000 0000 0000 0011 0000 0011 1001
                         
                   4   6   4   0   E   4   0   0
                0100 0110 0100 0000 1110 0100 0000 0000

   

• 问题2：对于65页补码加减法溢出的理解

• 问题2解决方案：先编写2.30中的函数原型，运行发现没有返回值。

• 
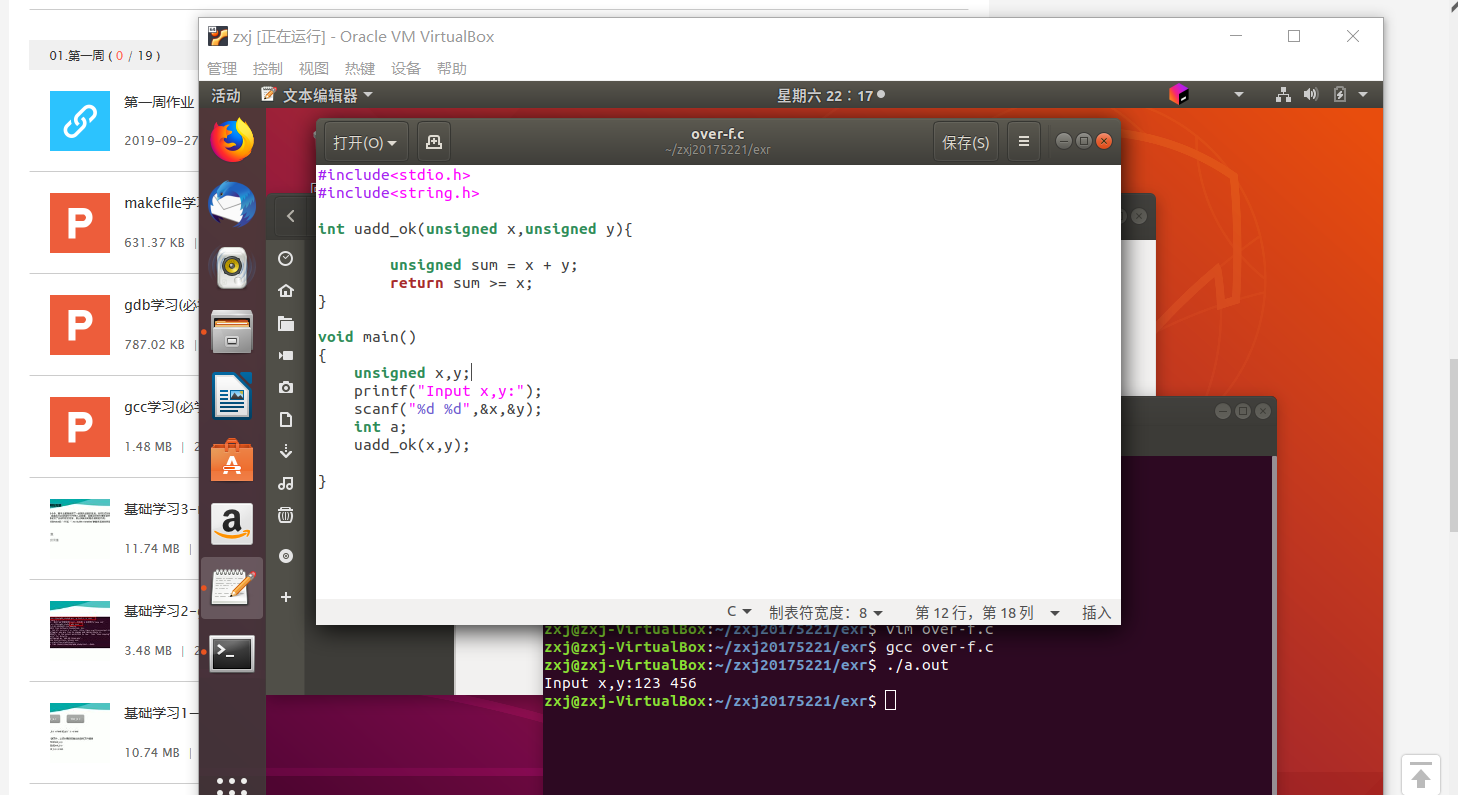
• 检查代码发现，是没有 print 结果，修改后运行
• 
• 
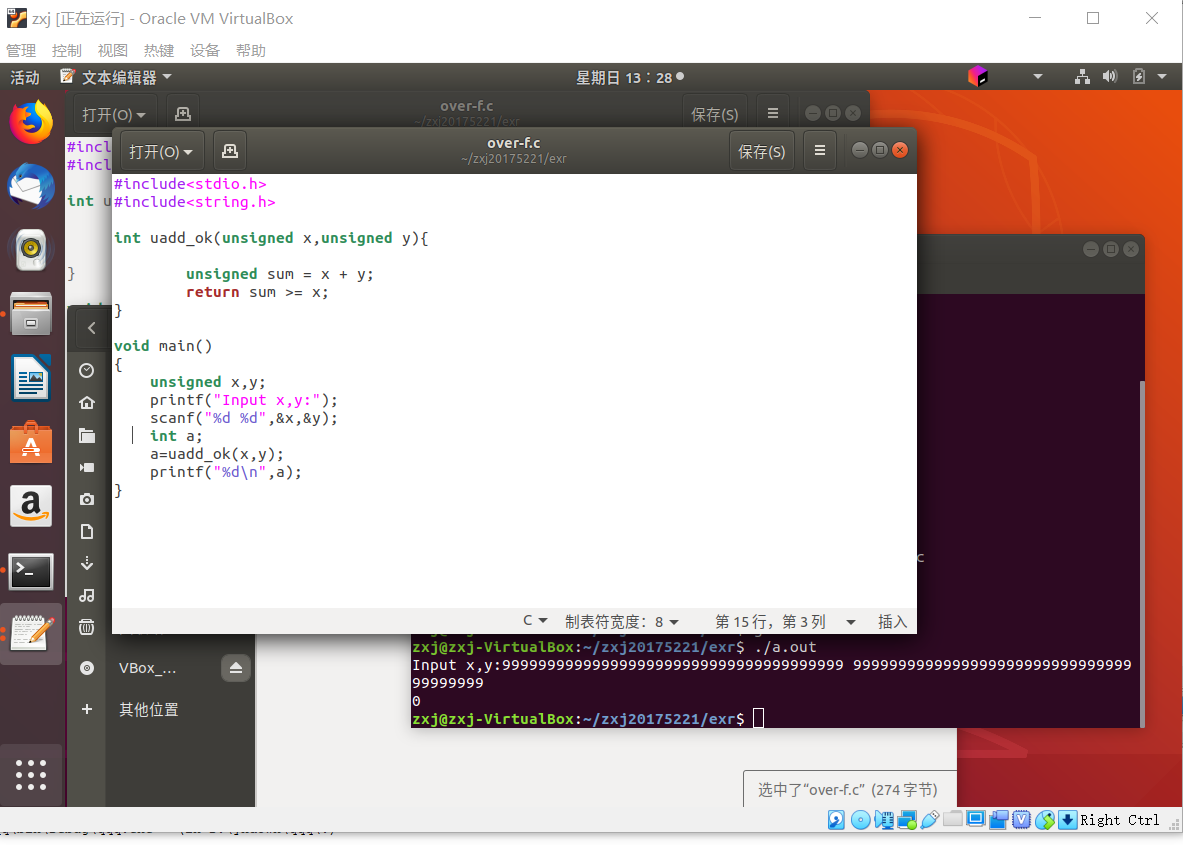
• 按照教材的讲法，补码加减同模运算挂钩
  以教材题目为例; 5/16 余数 5 ，21/16 余数 5，5和21同余 条件是(mod16)
  显然21对16进制数来说的话是溢出了 但是结果是对的  
• 而考虑教材中的“当两个异号数相加或者两个同号数相减是不会产生溢出的”，按照定义理解，如果运算结果比参加运算的数多一位，则溢出。但是CF保存着多出的一位，所以此运算并不算出错。
• 附上教材中的“正负溢出原理图”
• 

 

• 问题3：对2.11代码的修改以及2.10代码的数学分析

• 问题3解决方案：

• 教材中提到--对于任一向量a，有a^a=0。
• 将2.10与2.11的代码一同运行如下：
• 
• 
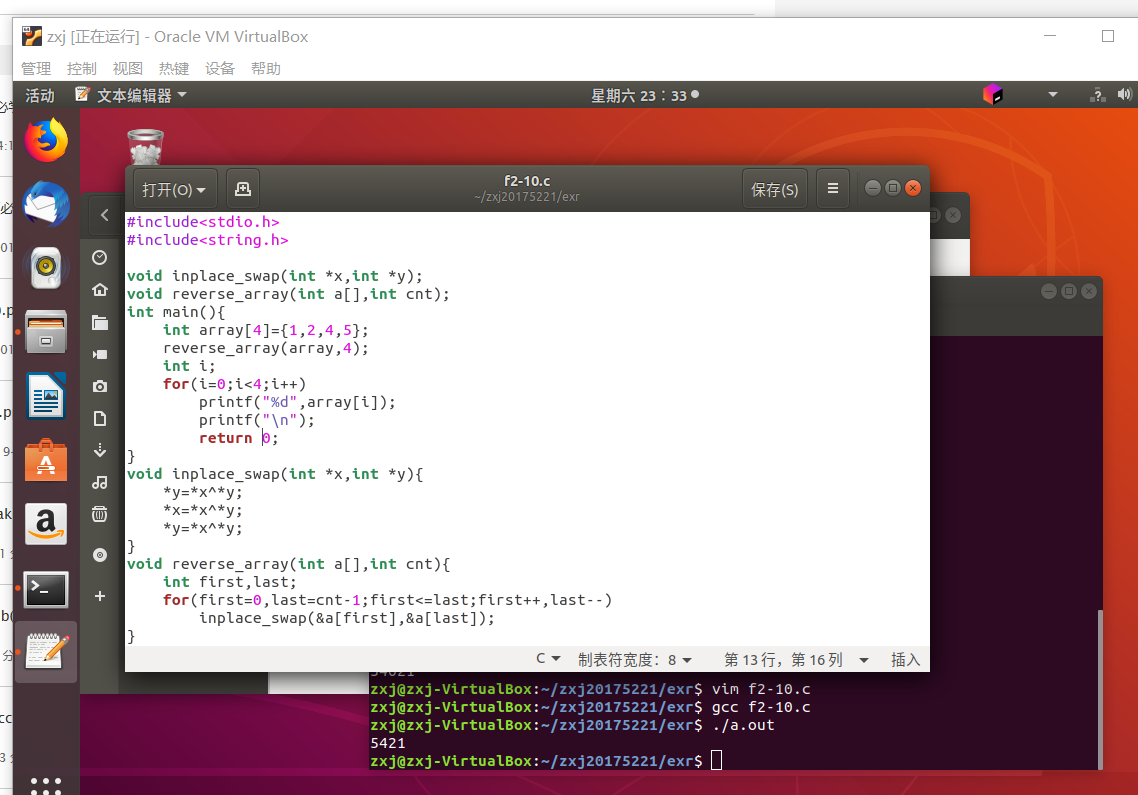
• 如教材中所讲，此般使用代码，偶数长度的数组可正常工作，但奇数长度的数组就把中间元素变为0
• 简单的数学分析可知
• 
• 知道哪里出问题了，寻找代码错误处，将 first<=last 修改为 first<last 即可
• 
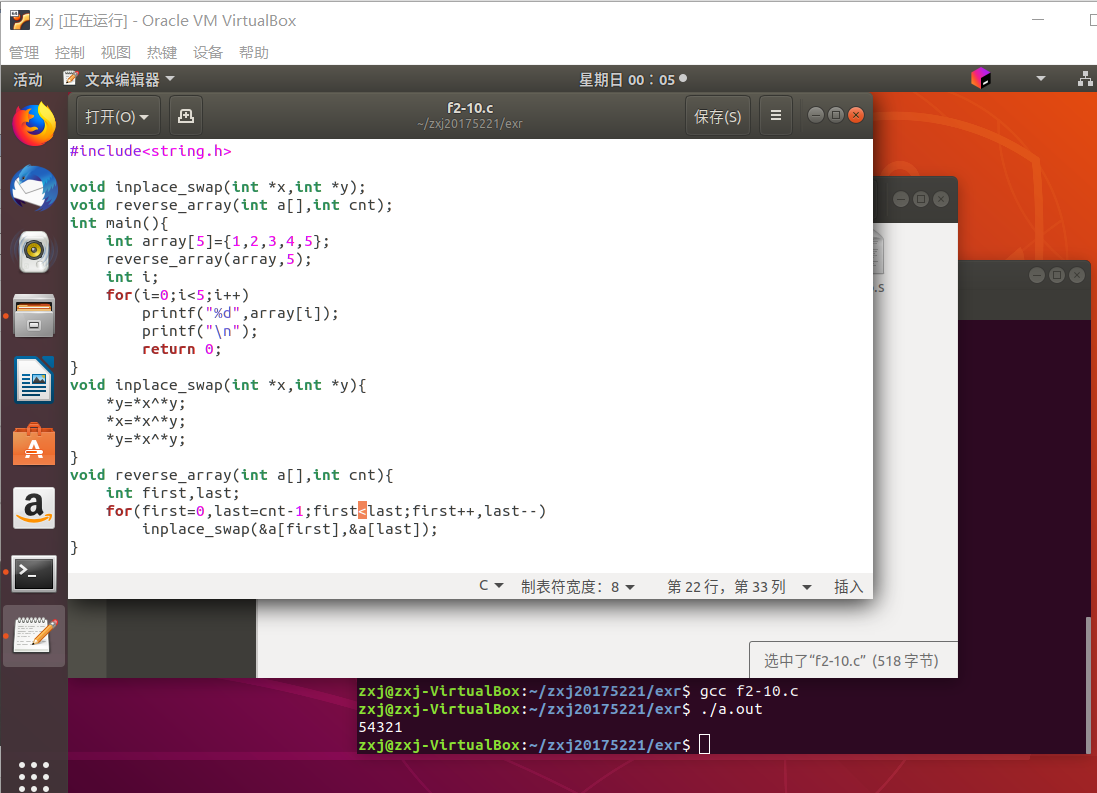
• 此时我回头研究2.10的代码是如何完成交换的

• void inplace_swap(int *x,int *y){
      *y=*x^*y;
      *x=*x^*y;
      *y=*x^*y;
  }

   

• 
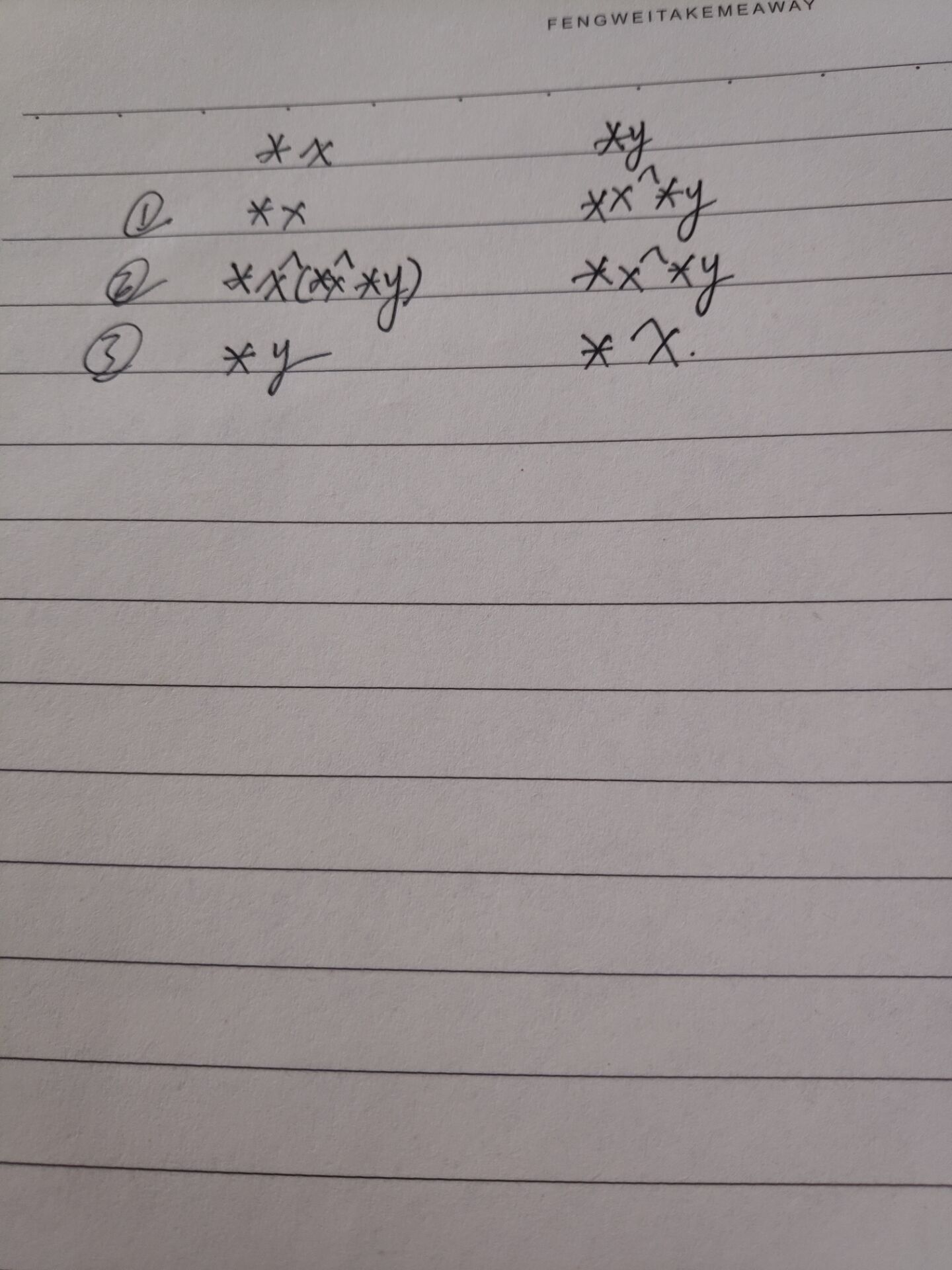
• 一开始想了很久，不知道x的step2是怎么走到step3的。才想起教材提示的：对于任一向量a，有a^a=0，想到可能是交换律，百度了一下，在向量^运算中的确也可以使用。于是便可知*x ^( *x ^ *y)=(*x ^ *x)^*y=0^*y=*y 
• 同理step3有 *y^(*x^*y)=*x ，我在此基础上对代码进行简单的删减以验证我的想法：运行的三次，依次是删减了step1,2,3
• 
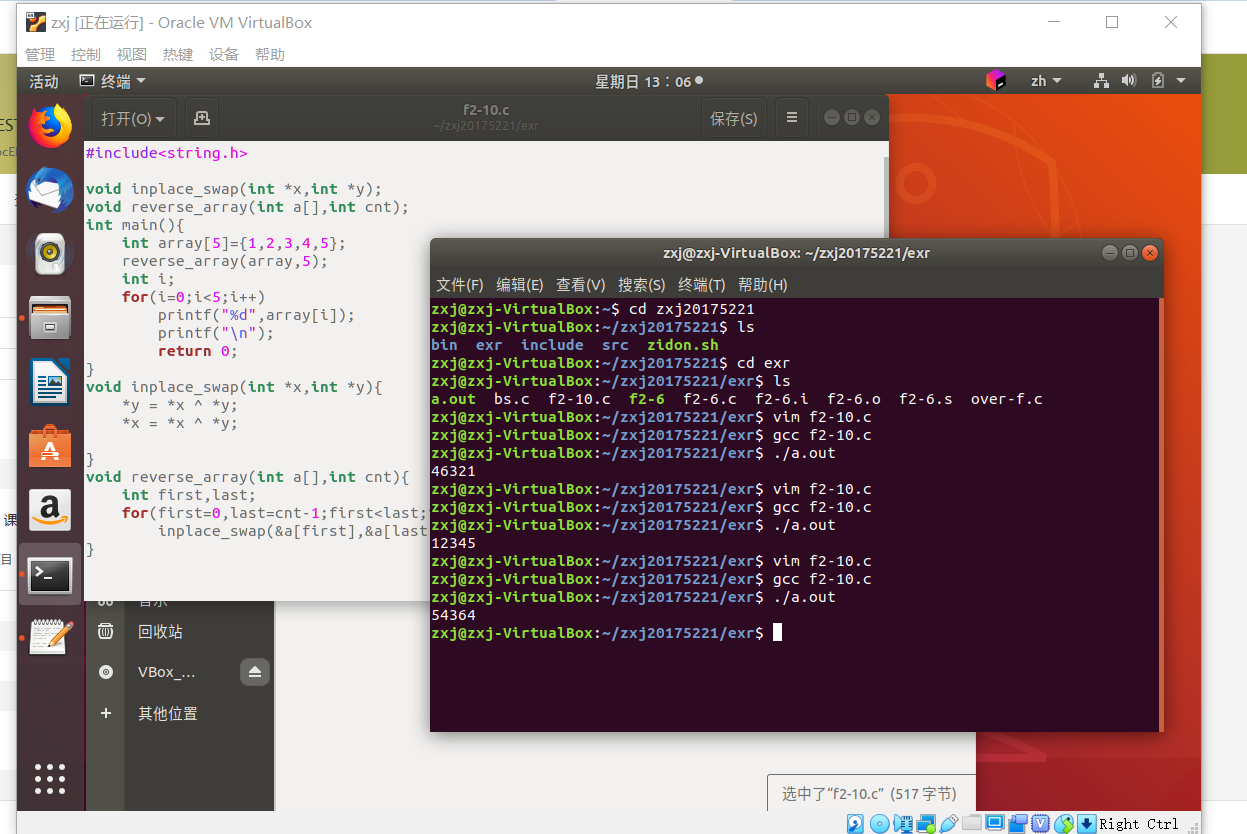
• 以删除step3为例，最终结果为 *x=*y，*y=*x^*y ，即前边的数替换为后边的数，而后边的数替换为两数的异或，猜想正确
• 如此便可理解教材中所说，这种交换方式同以往借用第三个位置来临时存储另一个值的方式不一样，并没有性能上的优势。它仅仅是一个智力游戏，或者按我说叫代数运算更亲切些。

• 问题4：2.31给出的程序是错误的示范，错在哪？

• 问题4解决方案：

• int tadd_ok(int x, int y)
  {
      int sum = x+y;
      return (sum-x == y)&&(sum-y == x);
  }

• 可以看出，这段代码的思路是，如果发生了溢出，那 (x+y)-y 的结果就不会等于x，且 (x+y)-x 的结果也不会等于y。但在实际测试中是，函数 tadd_ok()  的返回值总是 true，没有明白，我便上网查找了资料，发现： 即使加法产生了溢出，进行逆运算后的值依然等于参与运算的初值，即无论加法是否溢出，而（x+y)-y 总是会求值得到 x 也就是说，此运算是可逆的。而且补码加法会让其形成一个阿贝尔群，无论是否溢出，均满足sum-x==y且sum-y==x。
• 正确的解决办法为：

int tadd_ok(int x,int y){
int sum = x+y;
int neg_over = x < 0 && y < 0 && sum >= 0;
int pos_over = x >=0 && y >= 0 && sum < 0;
return !neg_over && !pos_over;
}

• 问题4：教材2.4.2的IEEE浮点表示如何理解

• 问题4解决方案：

• IEEE浮点标准：使用 V = (-1)^s * M * 2^E 的形式来表示一个数。其中s为符号；M为尾数，是一个二进制小数；E是阶码，用来对浮点数加权。
• 我们首先要对几个变量之间的关系牢记，公式按照教材给出如下：
• 

• 规格化值：
  Bias=2^(k-1)-1
  E=e-Bias
  M=1+f

   

• 非规格化值：
  Bias=2^(k-1)-1
  E=1-Bias
  M=f

   

• 阶码全为1，且小数域全为0时，得到的值表示无穷；小数域不全为0时，结果被称为 NaN(Not a Number) 
• 以教材图2-35为例，计算过程如下：
• 

 

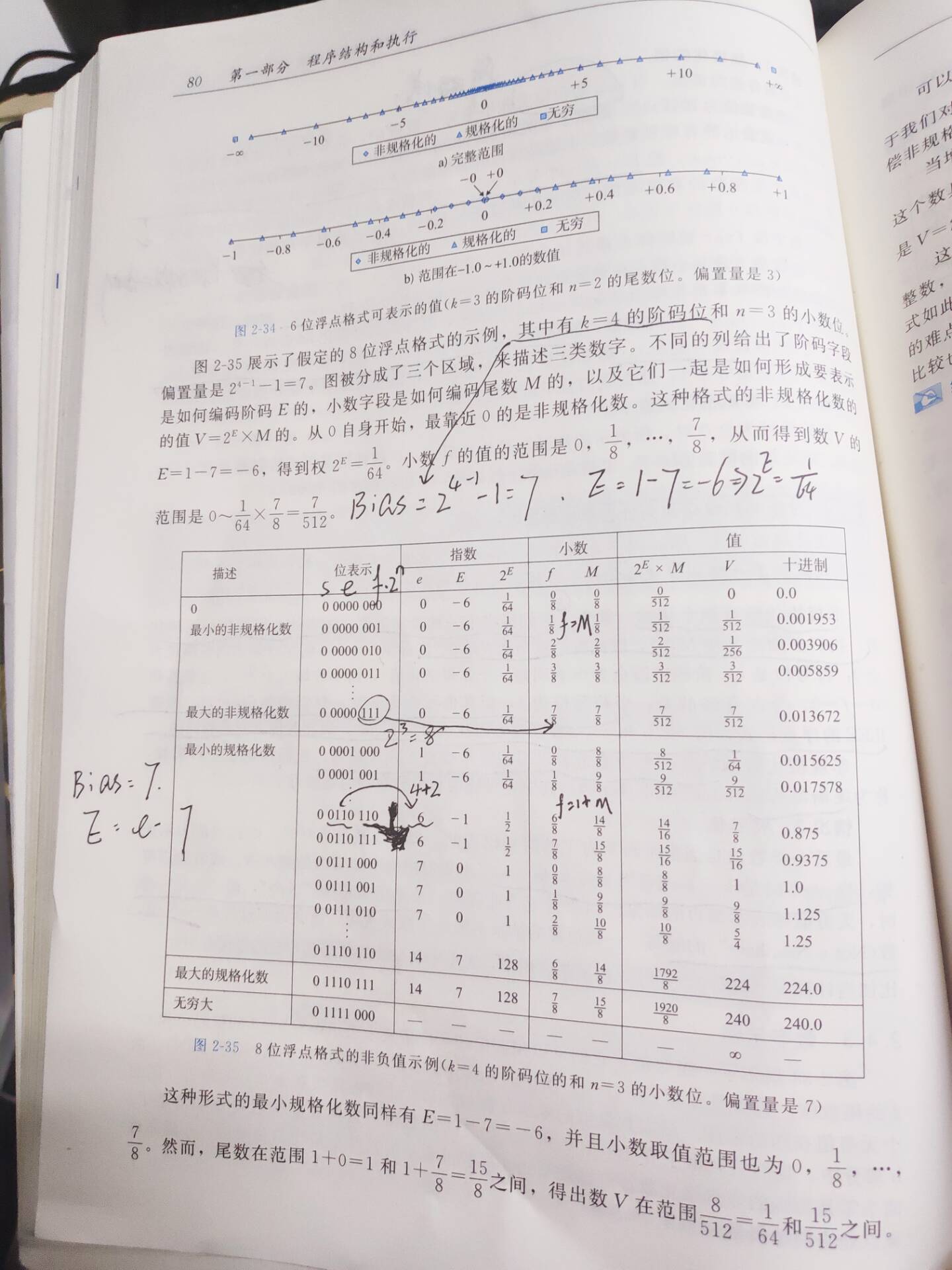
• 代码调试中的问题和解决过程

• 问题1：Linux下 od -tx -tc XXX 运行的结果与预想的不同

• 

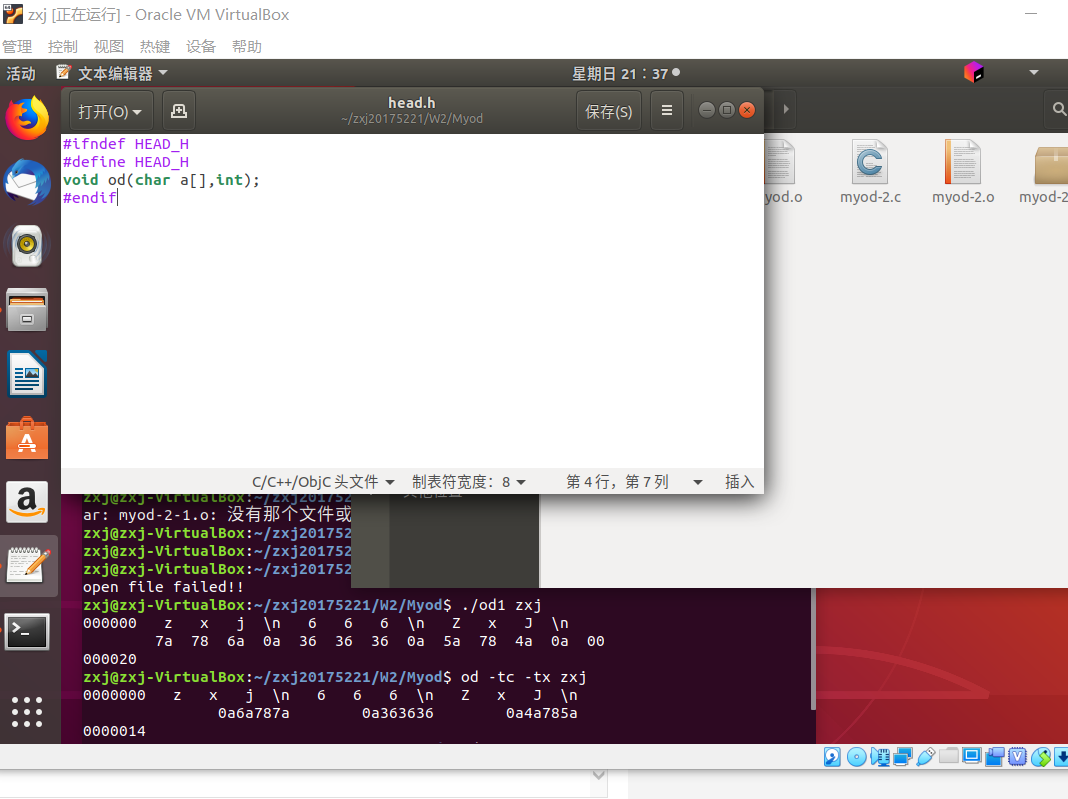
• 问题1解决方案：

• 这是我对 od -tc -tx 与 od -tc -tx1 实现的功能没太弄清楚导致的。在蓝墨云中的任务要求是 编写myod.c 用myod XXX实现Linux下od -tx -tc XXX的功能 ，实际查阅资料知， -tc 表示输出ASCII字符， -tx1 表示以十六进制输出，每组输出一字节，而若是 -tx ，默认的是四字节为一组。所以只需将命令改为 od -tc -tx1 zxj 即可
• 

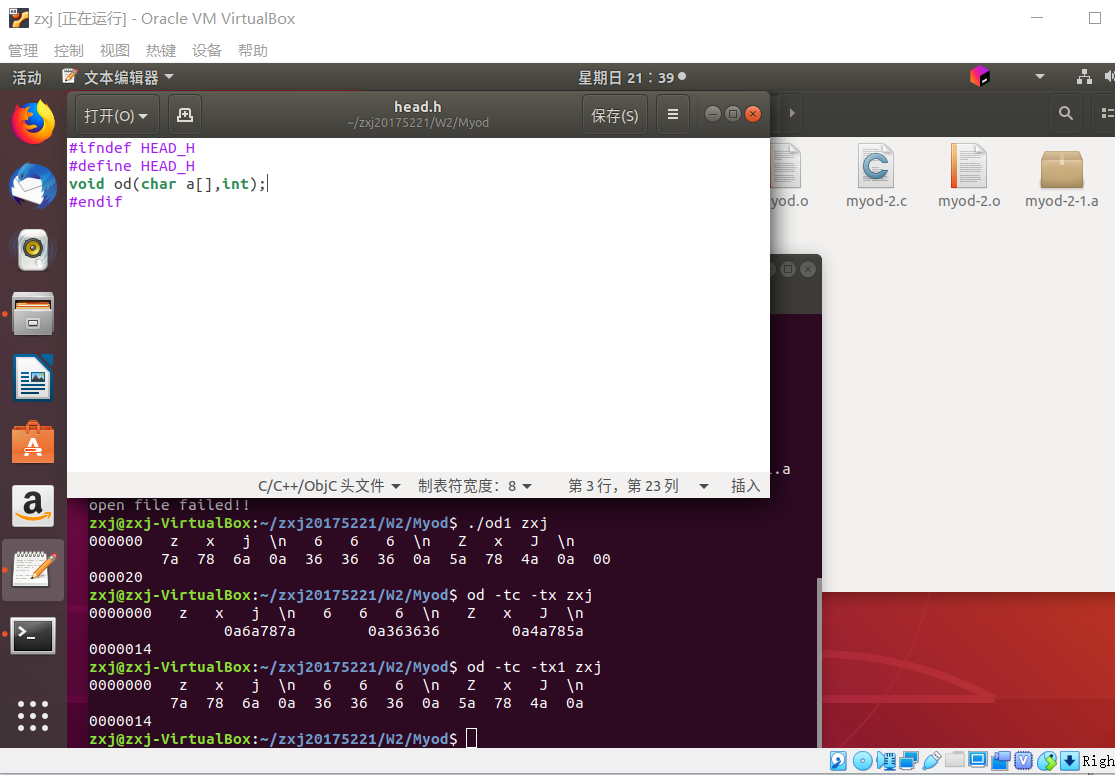
• 问题2：Linux中的od命令是可以显示 \n 的，但开始编写的C程序无法显示

• 问题2解决方案：参考了在ASCII码字符编码中,什么字符无法显示或打印出来 ，我们可以手动输出，遇到“\n”可使用转义字符，即 printf("\\n") .

• 代码托管

 

上周考试错题总结

无

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	53/53	1/1	20/20
第二周	200/253	1/2	21/20

尝试一下记录「计划学习时间」和「实际学习时间」，到期末看看能不能改进自己的计划能力。这个工作学习中很重要，也很有用。 耗时估计的公式 ：Y=X+X/N ，Y=X-X/N，训练次数多了，X、Y就接近了。

参考：软件工程软件的估计为什么这么难，软件工程 估计方法

• 计划学习时间:XX小时

• 实际学习时间:XX小时

• 改进情况：

(有空多看看现代软件工程 课件 软件工程师能力自我评价表)

参考资料

• 《深入理解计算机系统》
• 【编程基础】简单理解大小端那些事儿