蚁群算法MATLAB解TSP问题
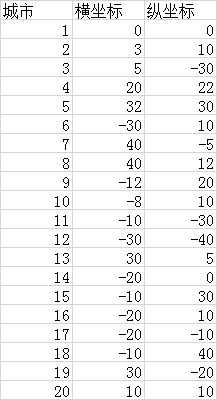
Excel表exp12_3_1.xls中数据为:
clc
clear all
[xdata,textdata]=xlsread('exp12_3_1.xls'); %加载20个城市的数据,数据按照表格中的位置保存在Excel文件exp12_3_1.xls中
x_label=xdata(:,2); %第二列为横坐标
y_label=xdata(:,3); %第三列为纵坐标
C=[x_label y_label]; %坐标矩阵
n=size(C,1); %n表示城市个数
D=zeros(n,n); %D表示完全图的赋权邻接矩阵,即距离矩阵D初始化
for i=1:n
for j=1:n
if i~=j
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5; %计算两城市之间的距离
else
D(i,j)=0; %i=j, 则距离为0;
end
end
end
%%==================蚁群算法实现过程======================================================
%%============== 第一步 变量初始化==============
iter_max=100; %最大迭代次数
m=30; % 蚂蚁个数
Alpha=1; % 表征信息素重要程度的参数
Beta=5; % 表征启发式因子重要程度的参数
Rho=0.8; % 信息素蒸发系数
Q=10; % 信息素增加强度系数
Eta=1./D; % Eta为能见度因数,这里设为距离的倒数
Tau=ones(n,n); % Tau为信息素矩阵,初始化全为1
Tabu=zeros(m,n); % 存储并记录路径的生成
nC=1; % 迭代计数器
R_best=zeros(iter_max,n); %各代最短路线,行为最大迭代次数,列为城市个数
L_best=inf.*ones(iter_max,1);%%各代最短路线的长度,inf为无穷大
L_ave=zeros(iter_max,1); % 各代平均路线长度
%%============== 第二步 将m只蚂蚁放到城市上==============
while nC<=iter_max %停止条件之一:达到最大迭代次数
Randpos=[];
for i=1:(ceil(m/n)) %ceil表示向无穷方向取整
Randpos=[Randpos,randperm(n)]; %randperm(n):表示随机产生一个整数排列
end
Tabu(:,1)=(Randpos(1,1:m))'; %每只蚂蚁(m只)都对应有一个位置,Tabu(:,1)为每只蚂蚁走过的第一个城市
%% ============== 第三步 m只蚂蚁按概率函数选择下一座城市,完成各自的周游==============
for j=2:n %城市从第二个开始
for i=1:m
visited=Tabu(i,1:(j-1)); %已访问的城市
J=zeros(1,(n-j+1)); %待访问的城市
P=J; %待访问城市的选择概率分布(初始化)
Jc=1; %循环下标
for k=1:n %利用循环求解待访问城市,如果第k个城市不属于已访问城市,则其为待访问城市
if length(find(visited==k))==0
J(Jc)=k;
Jc=Jc+1; %下表加1,便于下一步存储待访问的城市
end
end
for k=1:length(J) % 下面计算待访问城市的概率分布,length(J)表示待访问城市个数
P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta); %概率计算公式中的分子
end
P=P/(sum(P)); %概率分布:长度为待访问城市个数
Pcum=cumsum(P); %求累积概率和:cumsum([1 2 3])=1 3 6,目的在于使得Pcum的值总有大于rand的数
Select=find(Pcum>=rand); %按概率选取下一个城市:当累积概率和大于给定的随机数,则选择求和被加上的最后一个城市作为即将访问的城市
if isempty(Select) %若选择城市为空集,则随机将任一城市加入禁忌表中
Tabu(i,j)=round(1+(n-1)*rand);
else
next_visit=J(Select(1)); %next_visit表示即将访问的城市
Tabu(i,j)=next_visit; %将访问过的城市加入禁忌表中
end
end
end
if nC>=2;Tabu(1,:)=R_best(nC-1,:);end %若迭代次数大于等于2,则将上一次迭代的最佳路线存入到Tabu的第一行中
%% ==============第四步 记录本次迭代最佳路线==============
L=zeros(m,1);
for i=1:m;
R=Tabu(i,:);
for j=1:(n-1)
L(i)=L(i)+D(R(j),R(j+1)); %求路径距离
end
L(i)=L(i)+D(R(1),R(n)); %加上最后一个城市与第一个城市之间的距离
end
L_best(nC)=min(L); %最优路径为距离最短的路径
pos=find(L==L_best(nC)); %找出最优路径对应的位置:即为哪只蚂蚁
R_best(nC,:)=Tabu(pos(1),:); %确定最优路径对应的城市顺序
L_ave(nC)=mean(L); %求第k次迭代的平均距离
nC=nC+1;
%% ==============第五步 更新信息素,此处蚁周系统==============
Delta_Tau=zeros(n,n); %Delta_Tau(i,j)表示所有蚂蚁留在第i个城市到第j个城市路径上的信息素增量
for i=1:m
for j=1:(n-1) %建立了完整路径后在释放信息素
Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);
end
Delta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
end
Tau=(1-Rho).*Tau+Delta_Tau; %信息素更新公式
%% ==============第六步 禁忌表清零==============
Tabu=zeros(m,n);
end
%% ==============第七步 输出结果==============
Pos=find(L_best==min(L_best)); %找到L_best中最小值所在的位置
Shortest_Route=R_best(Pos(1),:) %提取最短路径
Shortest_Length=L_best(Pos(1)) %提取最短路径长度
%% ==============作图==============
figure(1) %作迭代收敛曲线图
x=linspace(0,iter_max,iter_max);
y=L_best(:,1);
plot(x,y,'-','LineWidth',2);
xlabel('迭代次数'); ylabel('最短路径长度');
figure(2) %作最短路径图
Shortest_Route=[Shortest_Route Shortest_Route(1)];
plot([C(Shortest_Route,1)],[C(Shortest_Route,2)],'o-');
grid on
for i = 1:size(C,1)
text(C(i,1),C(i,2),[' ' num2str(i)]);
end
xlabel('城市横坐标'); ylabel('城市纵坐标');



