hdu 2844 混合背包【背包dp】

http://acm.hdu.edu.cn/showproblem.php?pid=2844

题意：有n种纸币面额(a1,a2,...an),每种面额对应有(c1,c2,...cn)张。问这些钱能拼成1-m中多少种值。

题解：背包dp问题。若ci=1,是01背包，若ci*ai>=m则是完全背包，否则是多重背包。（详见《背包九讲》）

先复习一下三种简单背包形式：

　01背包（F[v] ← max{F[v], F[v −Ci] +Wi} ）：

　

　　

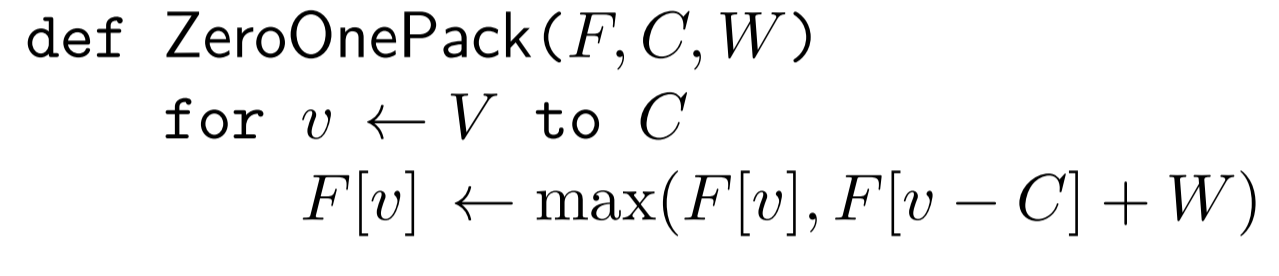
　完全背包（F[i, v] = max(F[i − 1, v], F[i, v −Ci] +Wi)）:

　 

　多重背包（利用二进制思想转化为01背包）：

　　

利用三种背包形式就可以轻松解决此题：

　　

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;

int f[100005];
int c[105],a[105];
int n,m;

void ZeroOnePack(int w,int v)
{
    for(int j=m;j>=v;j--)
        f[j]=max(f[j],f[j-w]+v);
}

void CompletePack(int w,int v)
{
    for(int j=v;j<=m;j++)
        f[j]=max(f[j],f[j-w]+v);
}

void MultiplePack(int w,int v,int c)
{
    int k=1;
    while(k<c)
    {
        ZeroOnePack(k*w,k*v);
        c=c-k;k*=2;
    }
    ZeroOnePack(c*w,c*v);
}

int main()
{
    while(scanf("%d%d",&n,&m)==2)
    {
        memset(f,0,sizeof(f));
        if(n==0) break;
        for(int i=1;i<=n;i++) scanf("%d",&a[i]);
        for(int i=1;i<=n;i++) scanf("%d",&c[i]);
        for(int i=1;i<=n;i++){
            if(c[i]==1)
                ZeroOnePack(a[i],a[i]);
            else if(c[i]*a[i]>=m)
                CompletePack(a[i],a[i]);
            else
                MultiplePack(a[i],a[i],c[i]);
        }
        int ans=0;
        for(int i=1;i<=m;i++)
            if(f[i]==i) ans++;
        printf("%d\n",ans);
    }
    return 0;
}