复杂度分析
一、什么是复杂度分析
- 数据结构和算法本身解决的是“快”和“省”的问题,衡量算法执行效率的指标就包括复杂度
- 复杂度分析包括时间复杂度和空间复杂度分析,时间复杂度是指算法执行的时间与数据规模的关系,空间复杂度是指算法占用的空间与数据规模的关系
二、为什么需要时间复杂度分析
- 通过测试、统计、监控,可以的得到算法执行的时间和占用的内存大小,但是测试结果非常依赖测试环境,测试结果受数据规模的影响很大
- 我们需要一个不依赖测试环境和数据规模就可以粗略估算算法执行效率的方法
三、如何进行复杂度分析
1.大O复杂度表示法
- 包括大O时间复杂度表示法和大O空间复杂度表示法
- 大O时间复杂度表示法表示代码执行时间随数据规模增长的变化趋势,又称渐进时间复杂度
- 大O空间复杂度表示法表示代码执行所占的内存空间随数据规模增长的变化趋势,又称渐进空间复杂度
2.时间复杂度分析法则
1). 所有代码的执行时间T(n)与每行代码的执行次数成正比
$T(n) = O(f(n))$
- n表示数据规模的大小
- f(n)表示每行代码执行的次数总和
- 大O表示代码的执行时间T(n)与f(n)表达式成正比
2). 只关注循环次数最多的一段代码
3). 加法法则:总的时间复杂度等于量级最大的那段代码的时间复杂度
$如果T1(n)=O(f(n)), T2(n)=o(g(n));那么T(n)=T1(n)+T2(n)=max(O(f(n)),O(g(n)))=O(max(f(n),g(n)))$
4). 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
$如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)T2(n)=O(f(n))O(g(n))=O(f(n)*g(n)).$
tips:复杂度分析关键在于“熟练”,无他,唯手熟尔
几种常见时间复杂度实例分析

分为两类:
- 非多项式量级:$O(2^n)$和$O(n!)$ 低效的算法
- 多项式量级 除非多项式量级剩下的全是多项式量级
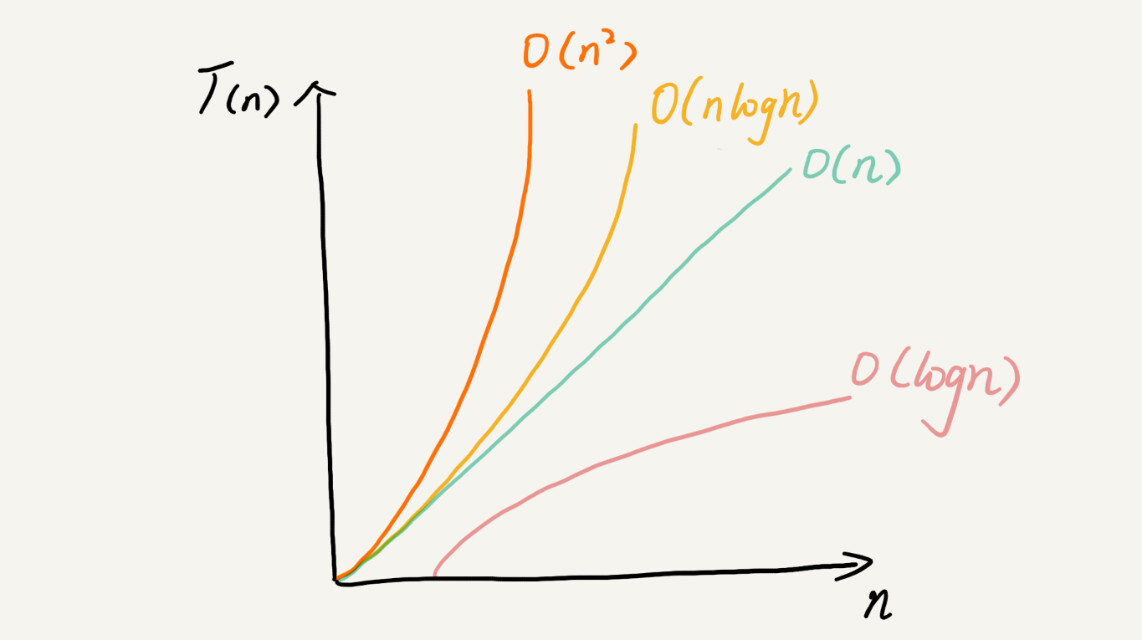
常见的复杂度有低阶到高阶有:$O(1),O(log(n)),O(n),O(nlogn),O(n^2)$
空间复杂度分析
空间复杂度全称渐进空间复杂度,表示算法的存储空间与数据规模之间的增长关系
四、最好、最坏、平均、均摊时间复杂度
- 最好情况时间复杂度:在最理想的情况下,执行这段代码的时间复杂度
- 最坏情况时间复杂度:在最糟糕的情况下,执行这段代码的时间复杂度
- 加权(期望)平均时间复杂度:代码在所有情况下执行次数的加权平均值表示
- 均摊时间复杂度:在代码执行的所有复杂度情况中绝大部分是低级别的复杂度,个别情况是高级别复杂度且发生具有时序关系时,可以将高级别复杂度用的时间均摊到低级别时间复杂度上,当低时间复杂度出现的概率远远大于高时间复杂度时,均摊的结果近似等于低时间复杂度。



