Codeforces Round #214 (Div. 2) C. Dima and Salad 背包

C. Dima and Salad

 

Dima, Inna and Seryozha have gathered in a room. That's right, someone's got to go. To cheer Seryozha up and inspire him to have a walk, Inna decided to cook something.

Dima and Seryozha have n fruits in the fridge. Each fruit has two parameters: the taste and the number of calories. Inna decided to make a fruit salad, so she wants to take some fruits from the fridge for it. Inna follows a certain principle as she chooses the fruits: the total taste to the total calories ratio of the chosen fruits must equal k. In other words, 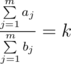 , where aj is the taste of the j-th chosen fruit and bj is its calories.

Inna hasn't chosen the fruits yet, she is thinking: what is the maximum taste of the chosen fruits if she strictly follows her principle? Help Inna solve this culinary problem — now the happiness of a young couple is in your hands!

Inna loves Dima very much so she wants to make the salad from at least one fruit.

Input

The first line of the input contains two integers n, k (1 ≤ n ≤ 100, 1 ≤ k ≤ 10). The second line of the input contains n integers a1, a2, ..., an (1 ≤ ai ≤ 100) — the fruits' tastes. The third line of the input contains n integers b1, b2, ..., bn (1 ≤ bi ≤ 100) — the fruits' calories. Fruit number i has taste ai and calories bi.

Output

If there is no way Inna can choose the fruits for the salad, print in the single line number -1. Otherwise, print a single integer — the maximum possible sum of the taste values of the chosen fruits.

Examples

input

3 2
10 8 1
2 7 1

output

18

Note

In the first test sample we can get the total taste of the fruits equal to 18 if we choose fruit number 1 and fruit number 2, then the total calories will equal 9. The condition 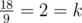 fulfills, that's exactly what Inna wants.

In the second test sample we cannot choose the fruits so as to follow Inna's principle.

 

 

题意：

　　给你n个水果，每个水果有两个属性ai,bi；

　　让你任选m个至少一个，使得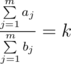   

　　注意是恰好整除为k

　　无方案输出-1，否则输出方案中分子最大的   那个分子

题解：

　　背包模型

　　先把式子化简看看，假设现在是X/Y=k

　　那么新加入的第i个水果造成 影响着是这样的 ： X = k*Y + k*bi - ai

　　那么久明显了，任意加入m个，我们使得后半段部分和为0即可，作DP

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N=1e6+110,mod=20090717,inf=2e9+10;

int n,k,a[N],b[N];
int dp[110][210000];
int main() {
    scanf("%d%d",&n,&k);
    for(int i = 1; i <= n; ++i) scanf("%d",&a[i]);
    for(int i = 1; i <= n; ++i) scanf("%d",&b[i]);
    for(int i  = 0; i <= n; ++i) {
        for(int j = 0; j <= 200000; ++j) dp[i][j] = -inf;
    }
    dp[0][100000] = 0;
    for(int i = 1; i <= n; ++i) {
        for(int j = k*b[i] - a[i]; j <= 200000; ++j) {
            dp[i][j] = max(dp[i][j],dp[i-1][j]);
            dp[i][j] = max(dp[i][j], dp[i-1][j - k*b[i] + a[i]] + a[i]);
        }
    }
    if(dp[n][100000] == 0) puts("-1");
    else
    cout<<dp[n][100000]<<endl;
    return 0;
}