BZOJ 1005 [HNOI2008]明明的烦恼 purfer序列,排列组合
1005: [HNOI2008]明明的烦恼
Description
自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?
Input
第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1
Output
一个整数,表示不同的满足要求的树的个数,无解输出0
Sample Input
3
1
-1
-1
1
-1
-1
Sample Output
2
HINT
两棵树分别为1-2-3;1-3-2
Source
题解:
n为树的节点数,d[ ]为各节点的度数,m为无限制度数的节点数。
则 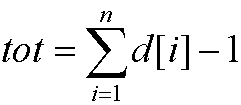
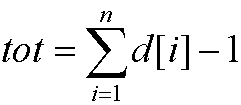
所以要求在n-2大小的数组中插入tot各序号,共有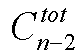 种插法;
种插法;
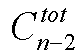 种插法;
种插法;在tot各序号排列中,插第一个节点的方法有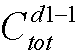 种插法;
种插法;
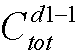 种插法;
种插法; 插第二个节点的方法有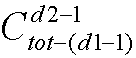 种插法;
种插法;
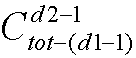 种插法;
种插法; ………
另外还有m各节点无度数限制,所以它们可任意排列在剩余的n-2-tot的空间中,排列方法总数为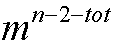 ;
;
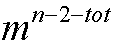 ;
;根据乘法原理:
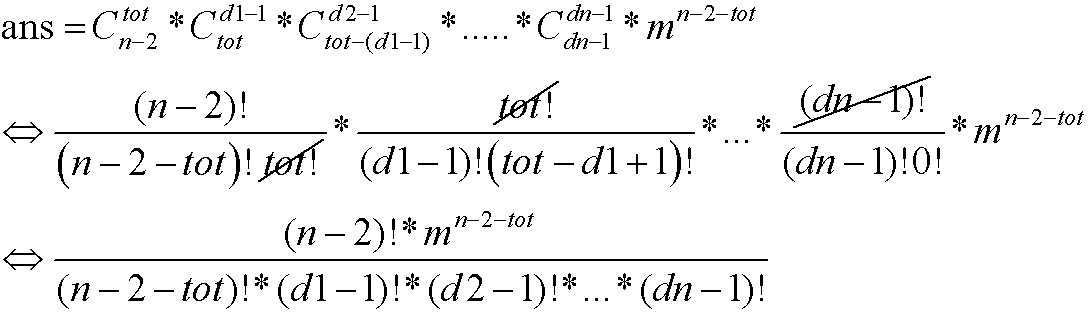
然后就要高精度了…..但高精度除法太麻烦了,显而易见的排列组合一定是整数,所以可以进行质因数分解,再做一下相加减。
关于n!质因数分解有两种方法,第一种暴力分解,这里着重讲第二种。
若p为质数,则n!可分解为 一个数*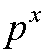 ,其中
,其中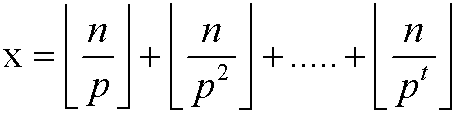 且
且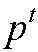 <n
<n
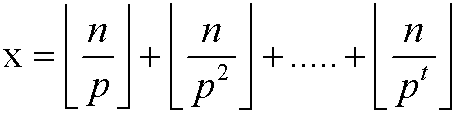 且
且所以 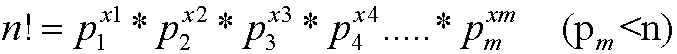
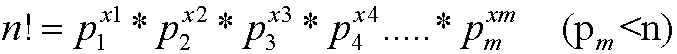
——转自怡红公子
#include <iostream> #include <cstdio> #include <cmath> #include <cstring> #include <algorithm> #include<vector> using namespace std; const int N = 1e5+10, M = 1e3+10, mod = 1000000, inf = 1e9+1000; typedef long long ll; int n; int d[N],ans[N]; int cnt[N],len=1; void go_way(int x,int key) { for(int j=2;j*j<=x;j++) { while(x%j==0) { cnt[j]+=key; x/=j; // cout<<j<<endl; } } cnt[x]+=key; } int sum = 0,m; void mul(int x) { for(int i=1;i<=len;i++) ans[i]*=x; for(int i=1;i<=len;i++) { ans[i+1]+=ans[i]/mod; ans[i]%=mod; } while(ans[len+1]>0) {len++;ans[len+1]+=ans[len]/mod;ans[len]%=mod;} } int main() { scanf("%d",&n); if(n==1) { int x; scanf("%d",&x); if(!x) cout<<1; else cout<<0; return 0; } for(int i=1;i<=n;i++) { scanf("%d",&d[i]); if(!d[i]) {cout<<0;return 0;} if(d[i]==-1) m++; else {d[i]--;sum+=(d[i]);} } if(sum > n-2) { cout<<0; return 0; } for(int i=1;i<=n-2;i++) go_way(i,1); for(int i=1;i<=n-2-sum;i++) { go_way(i,-1); } for(int i=1;i<=n;i++) { if(d[i]) for(int j=1;j<=d[i];j++) { go_way(j,-1); } } ans[1] = 1; for(int i=2;i<=n;i++) { for(int j=1;j<=cnt[i];j++) mul(i); } for(int i=1;i<=n-2-sum;i++) mul(m); for(int i=len;i>=1;i--) if(i==len)printf("%d",ans[i]); else printf("%06d",ans[i]); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号