UVALive 4192/HDU 2959 Close Enough Computations 数学

Close Enough Computations

 

Problem Description

The nutritional food label has become ubiquitous. A sample label is shown to the right. On the label the number of calories and the number of grams of fat, carbohydrate, and protein are given as integers.

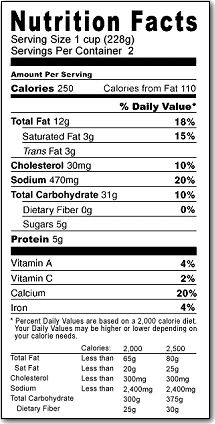
But carefully reading the label may cause the consumer to notice some inconsistencies. A gram of fat has 9 calories, a gram of carbohydrate has 4 calories, and a gram of protein has 4 calories. Consider the label to the right. A simple computation of the number of calories would indicate that the food should contain 12*9 + 31*4 + 5*4 or 252 calories, but the label indicates it has 250 calories.

While sometimes the difference in calories is due to other circumstances (such as the presence of alcohol or soluble fiber), this problem will consider only the possibility of round-off error. This food actually has 12.1 grams of fat (yielding 108.9 calories), 30.6 grams of carbohydrate (122.4 calories), 4.7 grams of protein (18.8 calories), so it does in fact have 250 calories (actually 250.1 calories).

Write a program that will determine if values for a nutritional label are consistent, that is, if there is a way the true values for the grams of nutrients can be rounded to the shown values and yield the number of calories shown.

You should assume that standard rounding rules apply; that is any value less than 0.5 rounds down and those 0.5 or over round up.

 

 

Input

The input will contain one or more sets of data about potential labels. Each data set will consist of 4 non-negative integers, separated by one or more blanks, on a single line. The integers represent the number of calories, the number of grams of fat, the number of grams of carbohydrates, and the number of grams of protein, in that order. The number of calories will not exceed 10000, and the number of grams of any component will not exceed 1000.

End of input is indicated by a line containing 4 zeroes. This line should not be processed.

 

 

Output

For each data set, print "yes" or "no" on its own line, indicating whether the given rounded values of the three nutrients can yield the given number of calories.

 

 

Sample Input

250 12 31 5 250 13 31 5 122 10 10 0 0 0 0 0

 

 

Sample Output

yes no no

 

题意：

  给你一个检验值，和三个参数值 这三个参数值 分别*9,*4,*4得到实际值，问你在 参数值可以与实际参数值大小相差在0.5内 的得到的实际值 

　检验该检验值是否符合标准

题解：

 我们把3个参数值都减或加0.5得到最小最大，只要判断 这个需要检验的值是否在 这个范围内就好了

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include<vector>
using namespace std ;
typedef long long ll;

const int  N = 100000 + 10;
const int mod = 1e9 + 7;

int main() {
    double sum,a,b,c;
    while(~scanf("%lf%lf%lf%lf",&sum,&a,&b,&c))  {
       if(sum == 0 && a == 0 && b == 0 && c == 0)break;
       double mi = max((a - 0.5),0.0) * 9 + max((b - 0.5),0.0) * 4 + max((c - 0.5),0.0) * 4;
       double ma = (a + 0.5) * 9 + (b + 0.5) * 4 + (c + 0.5) * 4;
       //printf("%lf %lf \n",sum,mi,ma);
       if(sum >= mi &&sum <=  ma) cout<<"yes"<<endl;
       else cout<<"no"<<endl;
    }
    return 0;
}