Codeforces Round #337 (Div. 2) C. Harmony Analysis 数学

C. Harmony Analysis

 

The semester is already ending, so Danil made an effort and decided to visit a lesson on harmony analysis to know how does the professor look like, at least. Danil was very bored on this lesson until the teacher gave the group a simple task: find 4 vectors in 4-dimensional space, such that every coordinate of every vector is 1 or  - 1 and any two vectors are orthogonal. Just as a reminder, two vectors in n-dimensional space are considered to be orthogonal if and only if their scalar product is equal to zero, that is:

.

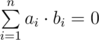
Danil quickly managed to come up with the solution for this problem and the teacher noticed that the problem can be solved in a more general case for 2k vectors in 2k-dimensinoal space. When Danil came home, he quickly came up with the solution for this problem. Can you cope with it?

Input

The only line of the input contains a single integer k (0 ≤ k ≤ 9).

Output

Print 2k lines consisting of 2k characters each. The j-th character of the i-th line must be equal to ' * ' if the j-th coordinate of the i-th vector is equal to  - 1, and must be equal to ' + ' if it's equal to  + 1. It's guaranteed that the answer always exists.

If there are many correct answers, print any.

Sample test(s)

input

2

output

++**
+*+*
++++
+**+

Note

Consider all scalar products in example:

• Vectors 1 and 2: ( + 1)·( + 1) + ( + 1)·( - 1) + ( - 1)·( + 1) + ( - 1)·( - 1) = 0
• Vectors 1 and 3: ( + 1)·( + 1) + ( + 1)·( + 1) + ( - 1)·( + 1) + ( - 1)·( + 1) = 0
• Vectors 1 and 4: ( + 1)·( + 1) + ( + 1)·( - 1) + ( - 1)·( - 1) + ( - 1)·( + 1) = 0
• Vectors 2 and 3: ( + 1)·( + 1) + ( - 1)·( + 1) + ( + 1)·( + 1) + ( - 1)·( + 1) = 0
• Vectors 2 and 4: ( + 1)·( + 1) + ( - 1)·( - 1) + ( + 1)·( - 1) + ( - 1)·( + 1) = 0
• Vectors 3 and 4: ( + 1)·( + 1) + ( + 1)·( - 1) + ( + 1)·( - 1) + ( + 1)·( + 1) = 0

 

题意：给 k，构造2^k * 2^k的图，  使得任意两行 相乘相加值为0

题解：对于一个  满足了条件的 正方形，想要得到将其边长翻倍的图形  我们将它复制接右边，接到正下方，再取反接到斜对角，就是了；

　　　　根据这个我们从1*1得到  2*2得到 4*4---到答案

 

//meek///#include<bits/stdc++.h>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<bitset>
#include<vector>
#include <queue>
#include <map>
#include <set>
#include <stack>
using namespace std ;
#define mem(a) memset(a,0,sizeof(a))
#define pb push_back
#define fi first
#define se second
#define MP make_pair
typedef long long ll;

const int N = 2000;
const int M = 1000001;
const int inf = 0x3f3f3f3f;
const int MOD = 1000000007;
const double eps = 0.000001;

int a[N][N],n;
int main() {
    scanf("%d",&n);
    a[0][0]=1;
    for(int x=1;x<=n;x++) {
        for(int i=0;i<(1<<x-1);i++) {
            for(int j=0;j<(1<<x-1);j++) {
                a[i][j+(1<<x-1)]=a[i][j];
                a[i+(1<<x-1)][j]=a[i][j];
                a[i+(1<<x-1)][j+(1<<x-1)]=1-a[i][j];
            }
        }
    }
    for(int i=0;i<(1<<n);i++) {
        for(int j=0;j<(1<<n);j++) {
            if(a[i][j])printf("+");
            else printf("*");
        }
        printf("\n");
    }
    return 0;
}