Codeforces Round #267 (Div. 2) C. George and Job DP

                                              C. George and Job

 

The new ITone 6 has been released recently and George got really keen to buy it. Unfortunately, he didn't have enough money, so George was going to work as a programmer. Now he faced the following problem at the work.

Given a sequence of n integers p1, p2, ..., pn. You are to choose k pairs of integers:

 

[l1, r1], [l2, r2], ..., [lk, rk] (1 ≤ l1 ≤ r1 < l2 ≤ r2 < ... < lk ≤ rk ≤ n; ri - li + 1 = m), 

in such a way that the value of sum 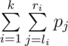 is maximal possible. Help George to cope with the task.

Input

The first line contains three integers n, m and k (1 ≤ (m × k) ≤ n ≤ 5000). The second line contains n integers p1, p2, ..., pn(0 ≤ pi ≤ 109).

Output

Print an integer in a single line — the maximum possible value of sum.

Sample test(s)

 

input

5 2 1
1 2 3 4 5

output

9

题意：给出一个数字序列，要求找出k个m长度不相交的区间，且区间数字之和最大

题解：dp[i][j]表示：

dp：dp[j][i]=max(dp[j-m][i-1]+sum[j]-sum[j-m],dp[j-1][i]);

//зїеп:1085422276
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <queue>
#include <typeinfo>
#include <map>
#include <stack>
typedef long long ll;
#define inf 100000000
#define mod 1000000007
using namespace std;

inline ll read()
{
    ll x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
//***************************************
ll sum[5004];
ll dp[5005][5005];
int main()
{
    int n,m,k,a[5005];
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        sum[i]=sum[i-1]+a[i];
    }
    for(int i=1;i<=k;i++)
    {
        for(int j=i*m;j<=n;j++){
            dp[j][i]=max(dp[j-m][i-1]+sum[j]-sum[j-m],dp[j-1][i]);
        }
    }
    cout<<dp[n][k]<<endl;
    return 0;
}