平衡树
普通平衡树
我们这里着重介绍一下 \(fhq\) \(treap\)。
首先我们会用一个结构体存下平衡树的节点。这道题中需要存左右儿子编号，优先度（随机的一个值），点上存的数是多少，子树中有多少数。我们记作 \(l,r,rd,da,siz\)。
接下来我们一个一个讲解函数：
\(newnode\) 新开点函数
考虑一个新点的五个值分别为 \(0,0,rand,val,1\)。代码：
int newnode(int val){
tr[++cnt]={0,0,rand(),val,1};
return cnt;
}
\(pushup\) 上传函数
事实上，只有 \(siz\) 需要上传，而一个点的 \(siz\) 显然是左右儿子的 \(siz\) 之和加上 \(1\)。代码：
void pushup(int p){
tr[p].siz=tr[tr[p].l].siz+tr[tr[p].r].siz+1;
}
\(split\) 分裂函数
同机房老哥写的 \(spilt\)，不好评价。
我们考虑按权值 \(val\) 分裂，因为 \(fhq\) \(treap\) 的点上存的值满足左儿子小于等于自己小于等于右儿子（定义），所以我们假设把原树分成 \(a\) 和 \(b\)，其中 \(a\) 上的值全部不大于 \(val\)，\(b\) 上的值全部大于 \(val\)。
首先如果遇到空节点直接返回即可。然后如果当前节点的值小于 \(val\)，那么把他和他的左子树划分给 \(a\)，递归分裂右子树；否则把他和他的右子树划分给 \(b\)，递归分裂左子树。最后在上传一下即可。代码：
void split(int p,int &a,int &b,int val){
if(p==0){
a=b=0;
return;
}
if(tr[p].da<=val){
a=p;
split(tr[p].r,tr[a].r,b,val);
}
else{
b=p;
split(tr[p].l,a,tr[b].l,val);
}
pushup(p);
}
\(merge\) 合并函数
首先基本对于所有数据结构的合并，都有在合并的两点其中一个为空时返回另一个（都空就返回空）。
然后我们维护的优先级 \(rd\) 就派上用场了，我们维护的时候把优先级小的放在上面（大的也无所谓）。
假设我们要合并 \(a,b\) 两棵树（前提条件 \(a\) 中的所有值小于 \(b\) 中的所有值，不难证明下文的所有用到 \(merge\) 的地方都满足此要求），不妨设 \(a\) 的 \(rd\) 更小，那么由于 \(b\) 中的值更大，我们把 \(b\) 合并在 \(a\) 的右子树，然后递归右子树并上传即可。反过来只需要合并在 \(b\) 的左子树即可。代码：
int merge(int a,int b){
if(!a||!b)return a+b;
if(tr[a].rd<tr[b].rd){
tr[a].r=merge(tr[a].r,b);
pushup(a);
return a;
}
else{
tr[b].l=merge(a,tr[b].l);
pushup(b);
return b;
}
}
\(ins\) 插入操作
因为下面的操作都比较简单，故代码统一在最后给出。
注意：所有在下文提到的原树按 \(val\) 分裂为 \(a,b\) 两树，均默认 \(a\) 中所有数小于 \(b\) 中所有数。
假设我们插入 \(val\) 这个值，于是我们先按 \(val\) 把原树分成 \(a,b\) 两树。然后把 \(val\) 这个单点合并到 \(a\) 中，最后再把 \(a,b\) 合回去。
\(del\) 删除操作
首先还是把原树按删除值 \(val\) 分成 \(a,b\)。然后考虑 \(val\) 在 \(a\) 最右边，于是再把 \(a\) 按 \(val-1\) 分成 \(la,ra\) 两棵树。
这时显然 \(ra\) 中有且仅有 \(val\) 一个值，所以考虑删除 \(ra\) 的根，一个经典的删除方法是，合并他的两个儿子。
最后再把所有东西原样合并回去即可。
\(getrk\) 查找排名操作
考虑把原树按照查找值 \(val\) 分成 \(a,b\)，于是答案就是 \(a\) 的 \(siz\) 再加 \(1\)（排名的定义），最后别忘了合并回去。
\(find\) 根据排名找数操作
考虑一个平衡树上二分，我们设查的排名为 \(rk\)，当前点的左子树大小为 \(siz\)。然后分类讨论一下：
-
\(siz=rk\)，返回当前点的值。
-
\(siz<rk\)，在右子树中 \(find(rk-siz)\)。
-
\(siz>rk\)，在左子树中 \(find(rk)\)。
\(getpre\) 查找前驱操作
考虑把原树按照 \(val-1\) 分成 \(a,b\)，于是 \(val\) 的前驱为 \(a\) 中最大的数，直接使用 \(find\) 函数查找即可。
\(getnxt\) 查找后继操作
考虑把原树按照 \(val\) 分成 \(a,b\)，于是 \(val\) 的后继为 \(b\) 中最小的数，仍然直接使用 \(find\) 函数查找即可。
完整代码：
#include<bits/stdc++.h>
#define int long long
#define N 100005
using namespace std;
struct fhq{
int rt,cnt;
struct node{
int l,r,rd,da,siz;
}tr[N];
int newnode(int val){
tr[++cnt]={0,0,rand(),val,1};
return cnt;
}
void pushup(int p){
tr[p].siz=tr[tr[p].l].siz+tr[tr[p].r].siz+1;
}
void split(int p,int &a,int &b,int val){
if(p==0){
a=b=0;
return;
}
if(tr[p].da<=val){
a=p;
split(tr[p].r,tr[a].r,b,val);
}
else{
b=p;
split(tr[p].l,a,tr[b].l,val);
}
pushup(p);
}
int merge(int a,int b){
if(!a||!b)return a+b;
if(tr[a].rd<tr[b].rd){
tr[a].r=merge(tr[a].r,b);
pushup(a);
return a;
}
else{
tr[b].l=merge(a,tr[b].l);
pushup(b);
return b;
}
}
void ins(int val){
int l,r;
split(rt,l,r,val);
rt=merge(merge(l,newnode(val)),r);
}
void del(int val){
int l,r,ll,lr;
split(rt,l,r,val);
split(l,ll,lr,val-1);
lr=merge(tr[lr].l,tr[lr].r);
rt=merge(merge(ll,lr),r);
}
int get_rk(int val){
int l,r;
split(rt,l,r,val-1);
int res=tr[l].siz+1;
rt=merge(l,r);
return res;
}
int find(int p,int rk){
int siz=tr[tr[p].l].siz+1;
if(siz==rk)return tr[p].da;
else if(siz<rk)return find(tr[p].r,rk-siz);
else return find(tr[p].l,rk);
}
int get_pre(int val){
int l,r;
split(rt,l,r,val-1);
int res=find(l,tr[l].siz);
rt=merge(l,r);
return res;
}
int get_nxt(int val){
int l,r;
split(rt,l,r,val);
int res=find(r,1);
rt=merge(l,r);
return res;
}
}fhq;
signed main(){
srand(time(0));
int n;
cin>>n;
while(n--){
int op,x;
cin>>op>>x;
if(op==1)fhq.ins(x);
else if(op==2)fhq.del(x);
else if(op==3)cout<<fhq.get_rk(x)<<'\n';
else if(op==4)cout<<fhq.find(fhq.rt,x)<<'\n';
else if(op==5)cout<<fhq.get_pre(x)<<'\n';
else cout<<fhq.get_nxt(x)<<'\n';
}
return 0;
}
文艺平衡树
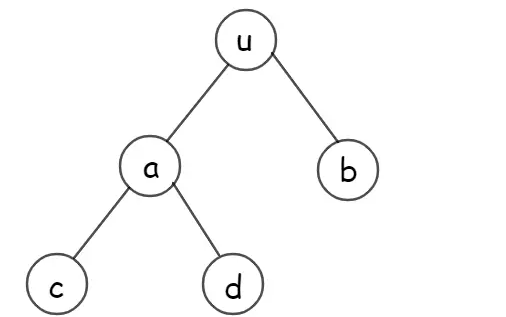
考虑这样一棵树，如果我们要输出他，就是输出他的中序遍历。
如果翻过来的话，就相当于反着输出中序遍历。
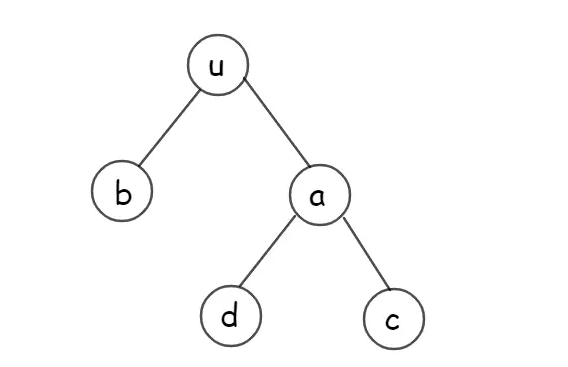
对于每一次操作，我们可以分裂出该区间代表的树，然后开始交换儿子。
但是发现这样巨慢无比，考虑线段树的区间修改也有这样的问题，于是我们打懒标记即可。
现在就只有一个问题，如何分裂出所在区间的树？考虑另一种经典的分裂：按照大小分裂。
我们每次分裂出前 \(siz\) 个数，这个过程可以使用平衡树上二分完成（注意这个二分和通常意义上的不同）。于是我们先分出前 \(l-1\) 个数，再在后一棵树中分出前 \(r-l+1\) 个数，然后打懒标记即可。
代码：
#include<bits/stdc++.h>
#define int long long
#define N 100005
using namespace std;
struct fhq{
struct node{
int l,r,rd,da,siz,lzy;
}tr[N];
int rt=0,cnt=0;
int newnode(int val){
tr[++cnt]={0,0,rand(),val,1,0};
return cnt;
}
void pushup(int p){
tr[p].siz=tr[tr[p].l].siz+tr[tr[p].r].siz+1;
}
void pushdown(int p){
if(!tr[p].lzy)return;
swap(tr[p].l,tr[p].r);
tr[tr[p].l].lzy^=1;
tr[tr[p].r].lzy^=1;
tr[p].lzy^=1;
}
void split(int p,int &a,int &b,int siz){
if(p==0){
a=b=0;
return;
}
pushdown(p);
if(tr[tr[p].l].siz+1<=siz){
a=p;
split(tr[p].r,tr[a].r,b,siz-tr[tr[p].l].siz-1);
}
else{
b=p;
split(tr[p].l,a,tr[b].l,siz);
}
pushup(p);
}
int merge(int a,int b){
if(!a||!b)return a+b;
if(tr[a].rd<tr[b].rd){
pushdown(a);
tr[a].r=merge(tr[a].r,b);
pushup(a);
return a;
}
else{
pushdown(b);
tr[b].l=merge(a,tr[b].l);
pushup(b);
return b;
}
}
void solve(int l,int r){
int x,y,yl,yr;
split(rt,x,y,l-1);
split(y,yl,yr,r-l+1);
tr[yl].lzy^=1;
rt=merge(x,merge(yl,yr));
}
void print(int p){
if(p==0)return;
pushdown(p);
print(tr[p].l);
cout<<tr[p].da<<' ';
print(tr[p].r);
}
}fhq;
signed main(){
srand(time(0));
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
fhq.rt=fhq.merge(fhq.rt,fhq.newnode(i));
}
while(m--){
int l,r;
cin>>l>>r;
fhq.solve(l,r);
}
fhq.print(fhq.rt);
return 0;
}
