关于BST、AVL、红黑树的学习
因为这段时间重新复习了数据结构的知识，学习到关于树与二叉树的应用时，进一步学习了之前没怎么在意的二叉搜索树（二叉排序树（BST）），二叉平衡树（AVL）。而之前看java中hashmap源码时了解到，在jdk1.7之前，hashmap是以数组+链表实现的，在jdk1.8之后便是用数组+红黑树来实现的，提高了查找的效率。所以这次把这三种树串起来一起学习。
- 首先说一下这三种树的关系，规则限制 红黑树>AVL>BST，平均查找长度（最坏情况）——红黑树，AVL（O(logn)） ——BST（O(n)）退化成了链表
- AVL是为了避免BST的高度过度增长，降低BST的性能，从而定了某些规则来限制避免树的高度增长过快
- 红黑树又相当于AVL树的一个扩展，一个子类，若AVL树频繁的删除或插入节点时，会导致AVL树的不平衡，从而频繁的做旋转，从而降低了性能，所以说AVL树比较适合做查找操作。而对于红黑树来说，虽然限制比较多一些，但是不会频繁的进行旋转，它有变色的功能，性能有所提升。红黑树旋转次数少，所以对于搜索，插入，删除操作较多的情况下，用红黑树。
AVL一定是二叉搜索树，且AVL规则限制很简单：它的左子树和右子树都是平衡二叉树，且左子树与右子树的高度差绝对值不超过1。AVL每次调整的对象都是最小不平衡子树，所以关键是找到最小不平衡子树，从而进行旋转。
AVL树在新节点插入后，造成查找路径上的某个节点不再平衡，则需要做出相应的调整，主要规则如下：
| 结点A的左孩子的左子树上插入了新节点，A的平衡因子由1增加至2，导致以A为根的子树失去平衡，需要一次向右旋转的操作 | LL平衡旋转（右单旋转） |
| 结点A的右孩子的右子树上插入了新节点，A的平衡因子由1增加至2，导致以A为根的子树失去平衡，需要一次向左旋转的操作 | RR平衡旋转（左单旋转） |
| 结点A的左孩子的右子树上插入了新节点，A的平衡因子由1增加至2，导致以A为根的子树失去平衡，需要进行两次旋转操作，一次先向左旋转的操作一次再向右旋转的操作 | LR平衡旋转（先左旋再右旋） |
| 结点A的右孩子的左子树上插入了新节点，A的平衡因子由1增加至2，导致以A为根的子树失去平衡，需要进行两次旋转操作，一次先向右旋转的操作一次再向左旋转的操作 | RL平衡旋转（先右旋再左旋） |
而红黑树又是特殊的AVL树，是对AVL树的一种扩展
主要性质如下：
- 根节点必须为黑丝；
- 父子节点不能同为红色；
- 从任何一个节点出发，到达叶子结点经过的黑色结点的数量一致；（此处的叶子结点是指NIL结点）
- 每个红色结点的两个子节点都是黑色，叶子结点都是黑色。
如果满足了以上的性质，就可以认为红黑色近似的平衡了。
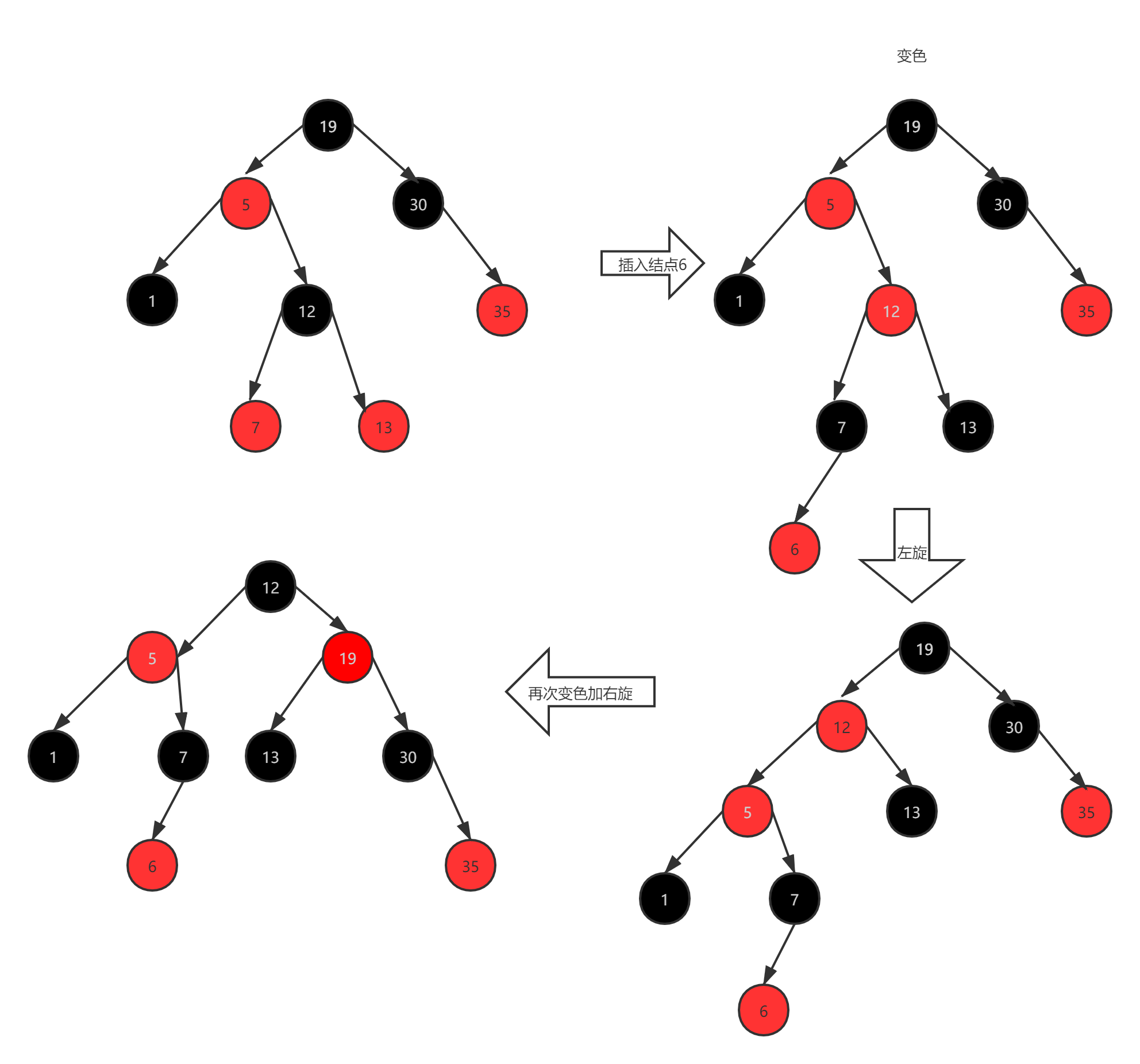
关于红黑树的插入，造成不平衡的情况，有以下旋转和颜色变换规则，与AVL有一些不同：
首先，默认插入的结点都是红色，之后再进行调整
