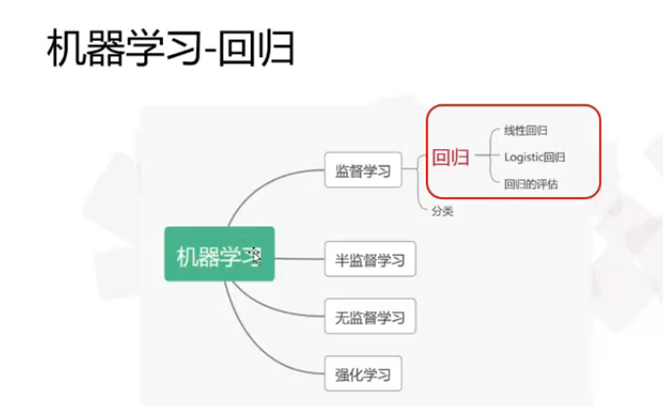
第五次作业：5.线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

（1）本节课的学习纲领：关于线性回归学习。

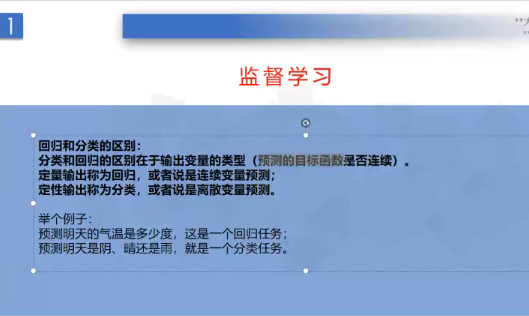
 （2）监督学习：关于回归与分类的理解。

 （3）线性回归定义：

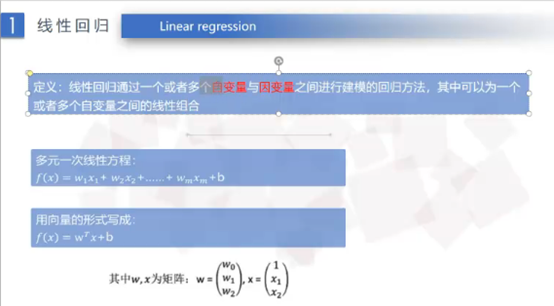
 （4）算法矩阵、数组：

数组：0/1/2/3维数组；3维数组为RGB。

矩阵：1.必须为二维数组；2.矩阵满足了特殊的运算的要求。

 （5）为了减少误差，引入了误差函数：

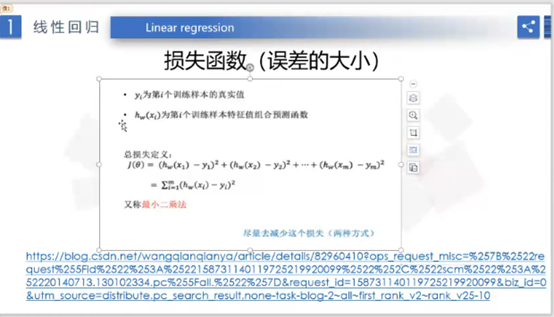
 学习网站：https://blog.csdn.net/wangqianqianya/article/details/82960410?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522158731140119725219920099%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=158731140119725219920099&biz_id=0&utm_source=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v25-10

（6）统计学习算法优化：(最小二乘法)1.正规方程；2.梯度下降。

 

梯度下降优化动态图：

循环10次，loss值变化如下：w、b逐渐靠近值12、4。

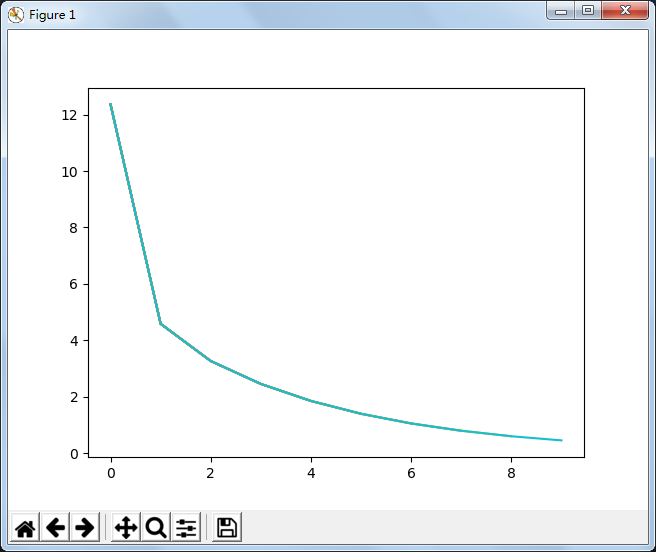
循环100次，loss值变化如下：w、b越靠近值12、4。

 

 

执行代码：

import random

import time

import matplotlib.pyplot as plt

 

#新建数据

_xs = [0.1 * x for x in range(0, 10)]

_ys = [12 * i + 4 for i in _xs]

print(_xs)

print(_ys)

w = random.random()   #权重

print(w)

b = random.random()   #偏置

print(b)

# y=wx+b

a1 = []

b1 = []

for i in range(10):

    for x, y in zip(_xs, _ys):  #遍历_xs和_ys

        print("x=",x,"y=",y)

        o = w * x + b           #预测值

        print("o=")

        e = (o - y)             #误差

        print("e=",e)

        loss = e ** 2           #损失函数

        dw = 2 * e * x

        db = 2 * e * 1

        w = w - 0.1 * dw        #梯度下降w

        b = b - 0.1 * db        #梯度下降b

        print('loss={0},w={1},b={2}'.format(loss, w, b))

    a1.append(i)

    b1.append(loss)

    plt.plot(a1, b1)

    plt.pause(0.1)

plt.show()

2.思考线性回归算法可以用来做什么？

答：线性回归是连续性变量预测，可预测具体房价、天气温度等连续性变化数据，用作预测工具，更科学、更准确地预测数据。