DS博客作业-图
0PTA截图
1.本周学习总结（6分）
定义：顶点集v与顶点间的关系，边集合E所组成的数据结构
-
无向图
-
有向图
1.1 图的存储结构
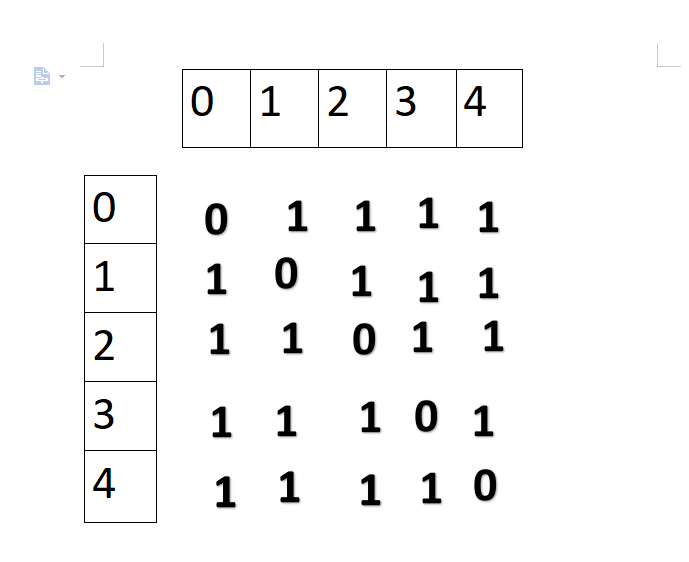
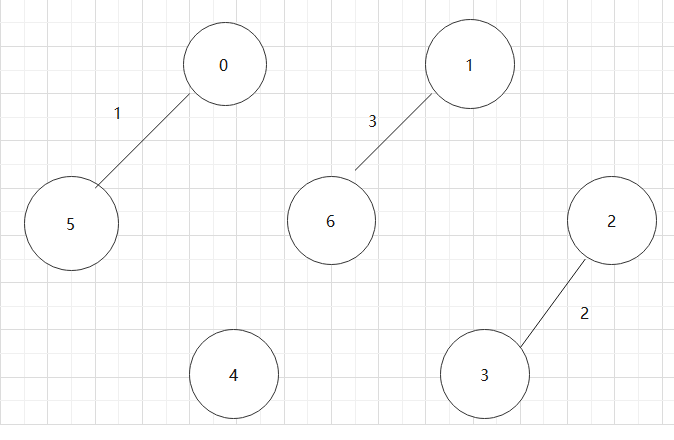
1.1.1 邻接矩阵（不用PPT上的图）
上图所对应的邻接矩阵：
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（邻接矩阵）存储图中的边或弧的信息。
设图G有n个顶点，则邻接矩阵是一个n*n的方阵
- 特点
1、图的邻接矩阵表示是唯一的
2、对于含有n个顶点的图，当采用邻接矩阵储存时，无论是有向图还是无向图，也无论边的数目是多少，其存储空间都为O（n^2),所以邻接矩阵适合于存储边的数目较多的稠密图
3、无向图的邻接矩阵一定是一个对称矩阵
4、对于无向图，邻接矩阵的数组的第i行或第i列非零元素，非无穷大元素的个数正好是顶点i的度
5、对于有向图，邻接矩阵数组的第i行或i列非零元素，非无穷大元素个数正好是顶点i的出度（或入读）。
6、在邻接矩阵中，判断图中两个顶点之间是否有边或者两个顶点之间边的权的执行时间为O（1），所以在需要提取边权值的算法中通常采用邻接矩阵存储结构。
结构体
#define MAXV<最大顶点个数>
#define INF32767//定义无穷大
typedef struct
{
int no;//顶点编号
InfoType info;//顶点的其他信息
}VertexType;//顶点的类型
typedef struct
{
int edges[MAXV][MAXV];//邻接矩阵数组
int n, e;//顶点数，边数
VertexType vexs[MAXV];//存放顶点信息
}MatGraph;
建图函数
void CreateMGraph(MGraph& g, int n, int e)//建图
{
int i, j, a,b;
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
g.edges[i][j] = 0;
for (i = 1; i <= e; i++)
{
cin >> a >> b;
g.edges[a][b] = 1;
g.edges[b][a] = 1;
}
g.n = n;
g.e = e;
}
1.1.2 邻接表
造一个图，展示其对应邻接表（不用PPT上的图）
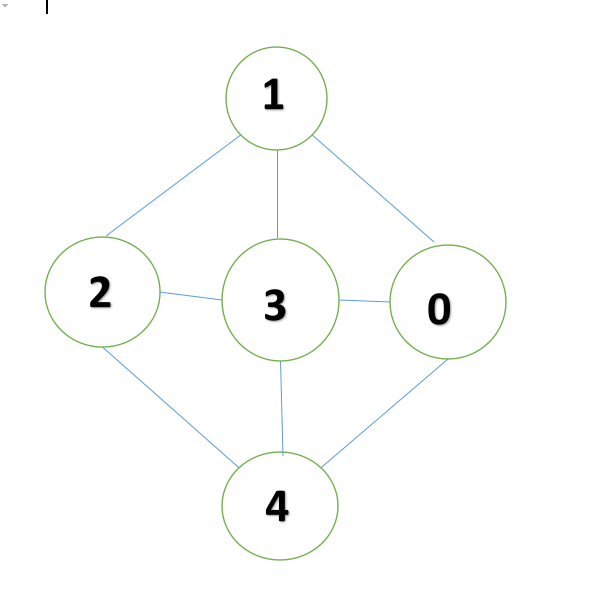
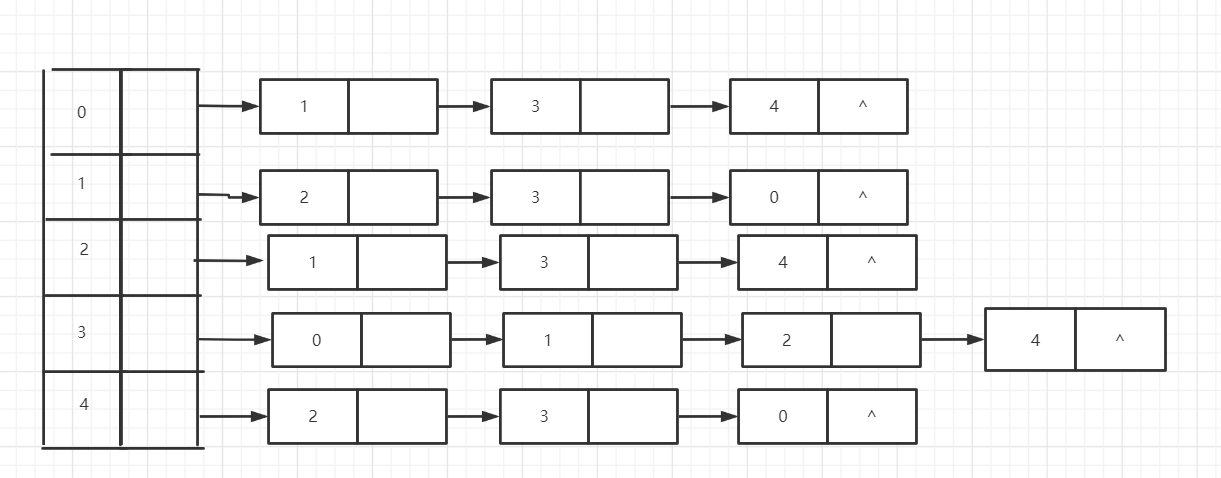
邻接矩阵的结构体定义
#define MAXV 20
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int info; //该边的相关信息，如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{ AdjList adjlist; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
建图函数
void CreateAdj(AdjGraph*& G, int n, int e)//创建图邻接表
{
int i;
int a, b;
G = new AdjGraph;//
G->e = e;
G->n = n;
for (i = 1; i <= n; i++)
{
G->adjlist[i].firstarc = NULL;
}
for (i = 1; i <= e; i++)
{
cin >> a>> b;
ArcNode* p, * q;
p = new ArcNode;
q = new ArcNode;
p->adjvex = b;
q->adjvex = a;
p->nextarc = G->adjlist[a].firstarc;
G->adjlist[a].firstarc = p;
q->nextarc = G->adjlist[b].firstarc;
G->adjlist[b].firstarc = q;
}
}
- 特点
1、邻接表的表示不唯一，因为每个顶点对应的单链表中各边结点的链接次序可以是任意的，取决于建立邻接表的算法以及边的输入顺序
2、对于有n个顶点和e条边的无向图，其邻接表有n个头节点，2e个边结点，而对于有向图，有有n个头节点，e个边结点，对边数目较少的稀疏图，邻接表比邻接矩阵更节省存储空间
3、对于无向图，邻接表中顶点i对应的第i个单链表的边结点数目正好是顶点i的度
4、对于有向图，邻接表中顶点i对应第i个单链表的边结点数目仅仅是顶点i的出度，顶点i的入度为邻接表中中所有adjvex域值为i的边结点数目
5、在邻接表中，查找顶点i关联的所有边是非常快速的，所以在需要提取某个顶点的所有邻接节点的算法中通常采用邻接表存储结构
1.1.3 邻接矩阵和邻接表表示图的区别
- 联系：邻接表中每个链头后的所有边表结点对应邻接矩阵中的每一行，邻接表中的每个边表结点对应邻接矩阵该行的一个非零元素。
- 适用图：邻接矩阵多用于稠密图的存储（e接近n（n－1）／2），而邻接表多用于稀疏图的存储（e＜＜n2）。
- 是否唯一：对于任一确定的无向图，邻接矩阵是唯一的（行列号与顶点编号一致），但邻接表不唯一（链接次序与顶点编号无关）。
- 空间复杂度：邻接矩阵的空间复杂度为0（n2），而邻接表的空间复杂度为0（n＋e）
- 找邻接点：在邻接表上容易找到任意一顶点的第一个邻接点和下一个邻接点，但要判定任意两个顶点（vi，vj）之间是否有边或弧相连，则需搜索第i个或第j个链表，还不及邻接矩阵方便。
1.2 图遍历
1.2.1 深度优先遍历
- 定义：从图中某顶点v出发：
（1）访问顶点v；
（2）依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问；
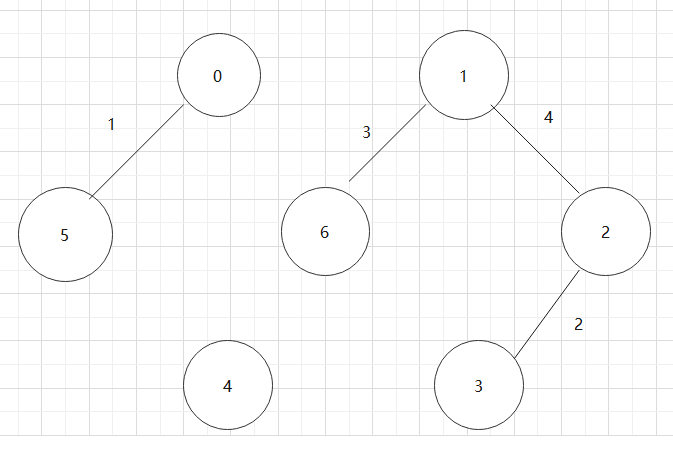
（3）若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。 当然，当人们刚刚掌握深度优先搜索的时候常常用它来走迷宫.事实上我们还有别的方法，那就是广度优先搜索(BFS). - 选上述的图，继续介绍深度优先遍历结果
深度遍历：0->1->2->3->6->4->5
深度遍历代码
* 邻接矩阵
void DFS(MGraph g, int v)//深度遍历
{
int i;
static int flag = 0;
if (visited[v] == 0)//
{
if (flag == 0)
{
cout << v;
flag ++;
}
else
{
cout << " " << v;
}
visited[v] = 1;//
}
for (i = 1; i <= g.n; i++)
{
if (g.edges[v][i] && visited[i] == 0)
DFS(g, i);
}
}
* 邻接表
void DFS(AdjGraph* G, int v)//v节点开始深度遍历
{
static int flag = 0;
ArcNode* p;
visited[v] = 1;
if (!flag)
{
cout << v;
flag = 1;
}
else
cout << " " << v;
p = G->adjlist[v].firstarc;//
while (p != NULL)
{
if (visited[p->adjvex] == 0)
DFS(G, p->adjvex);
p = p->nextarc;
}
}
深度遍历适用哪些问题的求解。（可百度搜索）
(1)、是否有简单路径?
假设图G采用邻接表存储，设计一个算法，判断顶点u到v是否有简单路径。
测试图结构及存储：
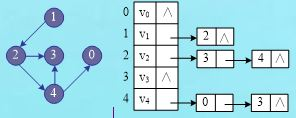
（2）、输出简单路径
问题：假设图G采用邻接表存储，设计一个算法输出图G中从顶点u到v的一条简单路径（假设图G中从顶点u到v至少有一条简单路径）。
（3）输出所有路径
问题：输出从顶点u到v的所有简单路径。
测试图结构及存储：
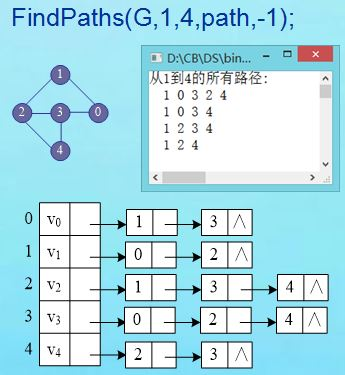
- 代码
//编写main函数，进行相关测试
#include <stdio.h>
#include <malloc.h>
#include "graph.h"
int visited[MAXV]; //定义存放节点的访问标志的全局数组
void FindPaths(ALGraph *G,int u,int v,int path[],int d)
//d是到当前为止已走过的路径长度，调用时初值为-1
{
int w,i;
ArcNode *p;
visited[u]=1;
d++; //路径长度增1
path[d]=u; //将当前顶点添加到路径中
if (u==v && d>1) //输出一条路径
{
printf(" ");
for (i=0; i<=d; i++)
printf("%d ",path[i]);
printf("\n");
}
p=G->adjlist[u].firstarc; //p指向u的第一条边
while(p!=NULL)
{
w=p->adjvex; //w为u的邻接顶点
if (visited[w]==0) //若顶点未标记访问，则递归访问之
FindPaths(G,w,v,path,d);
p=p->nextarc; //找u的下一个邻接顶点
}
visited[u]=0; //恢复环境
}
void DispPaths(ALGraph *G,int u,int v)
{
int i;
int path[MAXV];
for (i=0; i<G->n; i++)
visited[i]=0; //访问标志数组初始化
printf("从%d到%d的所有路径:\n",u,v);
FindPaths(G,u,v,path,-1);
printf("\n");
}
int main()
{
ALGraph *G;
int A[5][5]=
{
{0,1,0,1,0},
{1,0,1,0,0},
{0,1,0,1,1},
{1,0,1,0,1},
{0,0,1,1,0}
}; //请画出对应的有向图
ArrayToList(A[0], 5, G);
DispPaths(G, 1, 4);
return 0;
}
(4)输出一些简单回路
问题：输出图G中从顶点u到v的长度为s的所有简单路径。
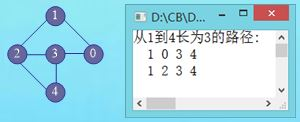
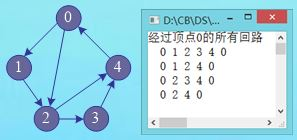
(5)输出通过一个节点的所有简单回路
问题：求图中通过某顶点k的所有简单回路（若存在）
测试图结构及存储：
1.2.2 广度优先遍历
- 定义：首先访问初始点v，接着访问顶点v的所有为访问的邻接点v1,v2,v3,.....vn，然后再按v1,v2,v3,.....vn的次序访问没一个顶点的所有未被访问的临界点，以此类推，直到图中所有和初始点v有路径相通的顶点都被访问过为止
- 选上述的图，继续介绍广度优先遍历结果
BFS:0->1->5->2->6->4->3
广度遍历代码
* 邻接表
void BFS(AdjGraph* G, int v) //v节点开始广度遍历
{
int temp,i;
ArcNode* p;
queue<int>q;
cout << v;
visited[v] = 1;
q.push(v);
while (!q.empty())
{
temp = q.front();
q.pop();
p = G->adjlist[temp].firstarc;
while (p != NULL)
{
if (visited[p->adjvex] == 0)
{
cout << " " << p->adjvex;
visited[p->adjvex] = 1;
q.push(p->adjvex);
}
p = p->nextarc;
}
}
}
* 邻接矩阵
void BFS(MGraph g, int v)//广度遍历
{
int t;
queue<int>q;
// if (visited[v] == 0)
// {
cout << v;
visited[v] = 1;
q.push(v);
// }
while (!q.empty())
{
t = q.front();
q.pop();
for (int j = 1; j <= g.n; j++)
{
if (g.edges[t][j] && visited[j] == 0)//
{
cout << " " << j;
visited[j] = 1;
q.push(j);
}
}
}
}
广度遍历适用哪些问题的求解。（可百度搜索）
通常用于求解无向图的最短路径问题
1 用队列保存与当前节点直接相连的节点
2 用数组记录每个节点是否遍历过，防止重复遍历
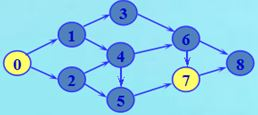
（1）最短路径
问题：求不带权连通图G中从顶点u到顶点v的一条最短路径。
测试用图结构：
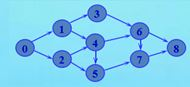
（2）最远顶点
问题：求不带权连通图G中，距离顶点v最远的顶点k
测试用图结构：
1.3 最小生成树
用自己语言描述什么是最小生成树。
对于一个带有权值的图所生成树，可以有很多种不同的情况，其中有一个树所生成的树带有的权值之和最小，就是最小生成树
- 生成最小生成树的准则：
1、必须只使用改图中的边来构造最小生成树，
2、必须使用且仅使用n-1条边来连接图中的n个顶点
3、不能使用产生回路的边
1.3.1 Prim算法求最小生成树
- 步骤
1、初始化U={v},以v到其他顶点的所有边为候选边
2、重复以下步骤n-1次，使得其他n-1个顶点被加入到u中：
（1）从侯选边中挑选权值最小的边加入TE，设改边在V-U中的顶点式k，将k加入U中
（2）考察当前U-V中的所有顶点j，修改候选边，若（k,j)的权值小于原来顶点j关联的侯选边，则用（k,j)取代后者作为侯选边
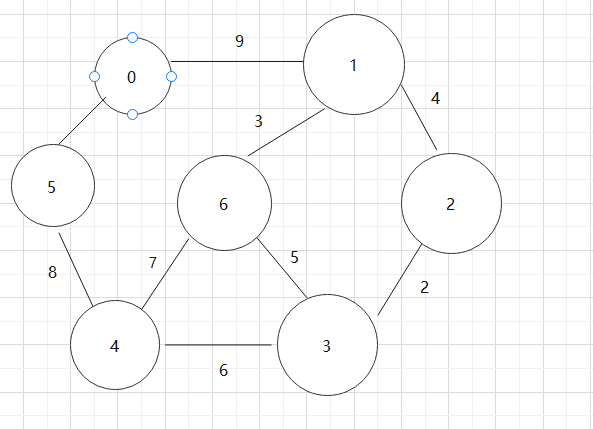
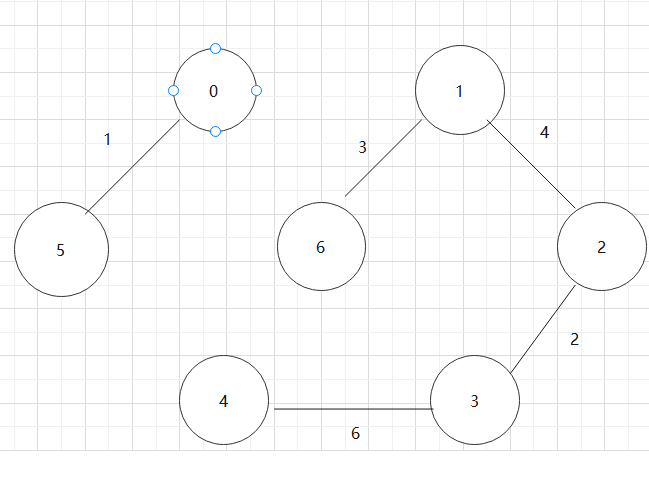
基于上述图结构求Prim算法生成的最小生成树的边序列
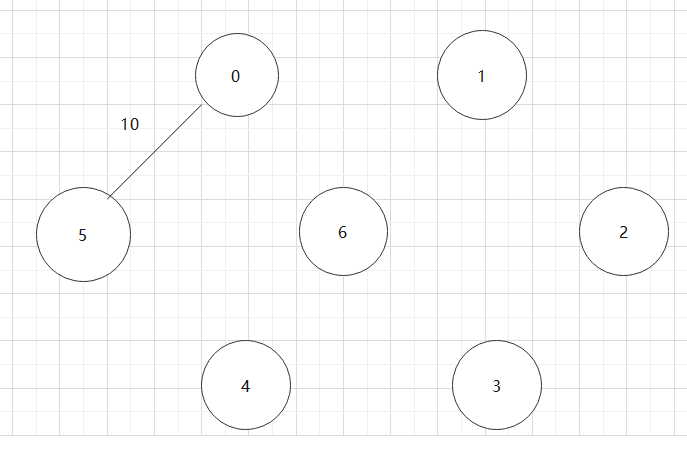
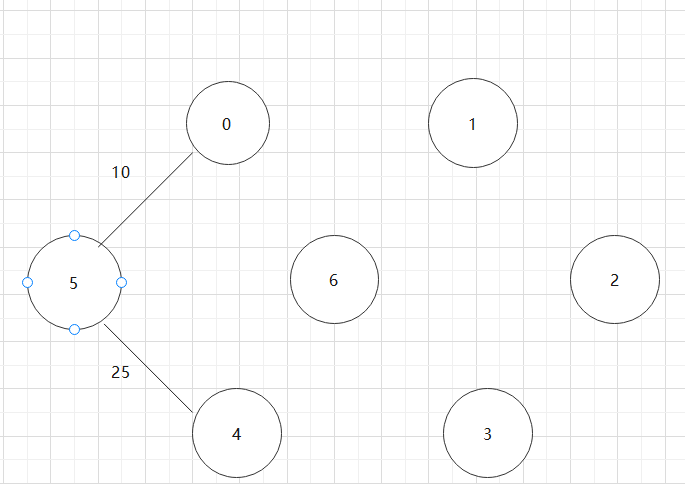
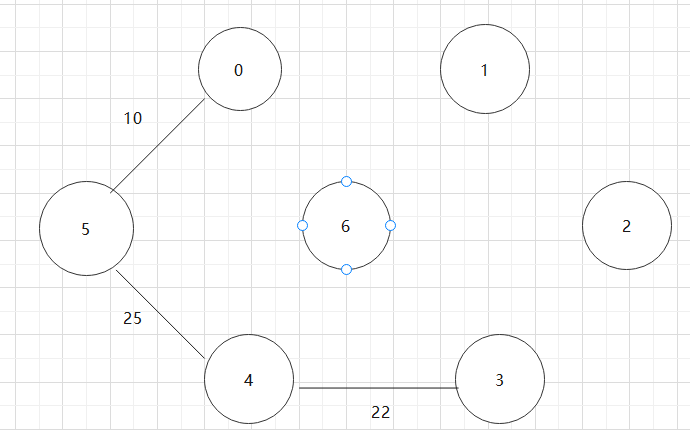
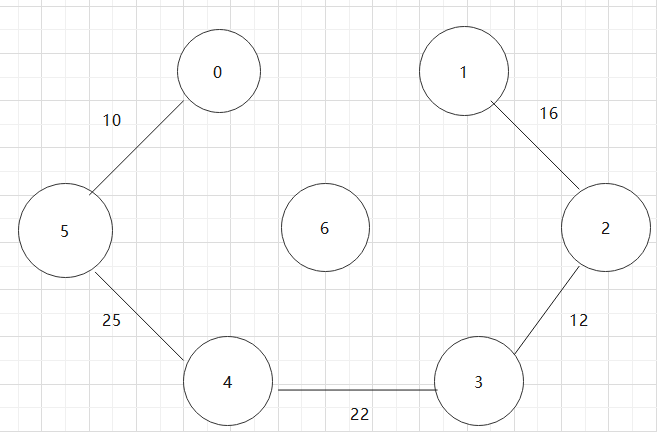
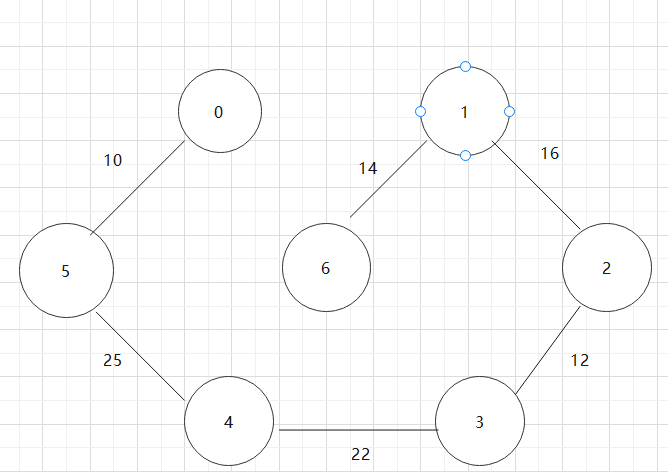
实现Prim算法的2个辅助数组是什么？其作用是什么？Prim算法代码。
closest[]:最小边
lowcost[]:存储最小边的权值
- 代码
void Prime(MGraph g)
{
int lowcost[3003];
int closest[3003];
int i, j, k;
int min = INF;
int num = 0;
for (i = 1; i <= g.n; i++)
{
lowcost[i] = g.edges[1][i];//置初值
closest[i] = 1;
}
for (i = 1; i < g.n; i++)
{
min = INF;
for (j = 1; j <= g.n; j++)//
{
if (lowcost[j] != 0 && lowcost[j] < min)
{
min = lowcost[j];//k记录最近顶点编号
k = j;
}
}
if (min == INF)
{
cout << -1;
return;
}
num = num + min;
lowcost[k] = 0;//标记k已加入
for (j = 1; j <= g.n; j++)
{
if (g.edges[k][j] != 0 && g.edges[k][j] < lowcost[j])//修正数组lowcost,closest
{
lowcost[j] = g.edges[k][j];
closest[j] = k;
}
}
}
cout << num;
}
分析Prim算法时间复杂度，适用什么图结构，为什么？
有两重循环，所以时间复杂度为O(n^2),
因为执行时间和图中的边数e无关，所以适用于稠密图求最小生成树
1.3.2 Kruskal算法求解最小生成树
- 步骤：假设连通网G=（V，E），令最小生成树的初始状态为只有n个顶点而无边的非连通图T=（V，{}），图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点分别在T中不同的连通分量上，则将此边加入到T中；否则，舍去此边而选择下一条代价最小的边。依此类推，直至T中所有顶点构成一个连通分量为止
基于上述图结构求Kruskal算法生成的最小生成树的边序列
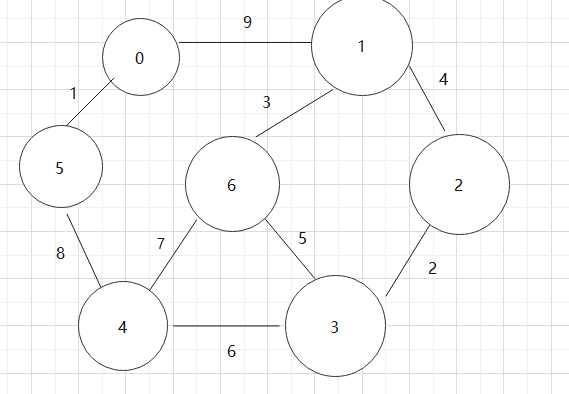
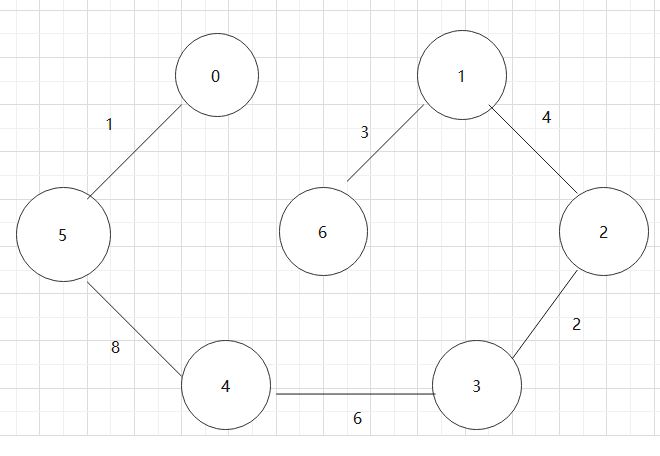
实现Kruskal算法的辅助数据结构是什么？其作用是什么？Kruskal算法代码。
采用邻接矩阵存储图，
数组vest[]记录一个顶点i所在的连通分量编号
结构体：存放边的初始顶点，边的终止顶点，边的权值
结构体数组E[]：存放图中所有的边
- 代码
typedef struct
{
int u;//边的起点
int v;//边的终止起点
int w;//边的权值
}Edge;
void Kruskal(MatGraph g)
{
int i,j,k,u1,v1,sn1,sn2;
UFSTree t[MaxSize];
Edge E[MaxSize];
k=1;
for(i=0;i<g.n;i++)
for(j=0;j<=i;j++)
if(g.edges[i][j]!=0&&g.edges[i][j]!=INF)
{ E[k].u=i; E[k].v=j;E[k].w=g.edges[i][j]; k++;}
HeapSort(E,g.e);//采用对排序对E数组按权值递增排序
MAKE_SET(t,g.n);//初始化并查集树t
k=1;//k表示当前构造生成树的第几条边，初值为1
j=1;//E中边的下标从1开始
while(k<g.n)//生成的边数小于n时循环
{
u1=E[j].u;
v1=E[j].v;//取一条边的头尾顶点编号u1和v2
sn1=FIND_SET(t,u1);
sn2=FIND_SET(t,v1);//分别得到两个顶点所属的集合编号
if（sn1!=sn2)
{ printf("(%d,%d):%d\n",u1,v1,E[j].w);
k++;//生成边数加1
UNION（t，u1,v1);//将u1和v1两个顶点合并
}
j++;
}
}
分析Kruskal算法时间复杂度，适用什么图结构，为什么？
时间复杂度：O（e*loge2 e),
因为算法执行时间仅与图中的边数有关，与顶点数无关，所以它特别适用稀疏图求最小生成树。
1.4 最短路径
1.4.1 Dijkstra算法求解最短路径
- 特点
1、在执行中，一个顶点一旦添加到S中，其最短路径长度不再改变
2.按顶点进入S的先后顺序最短路径长度越来越长
基于上述图结构，求解某个顶点到其他顶点最短路径。（结合dist数组、path数组求解）
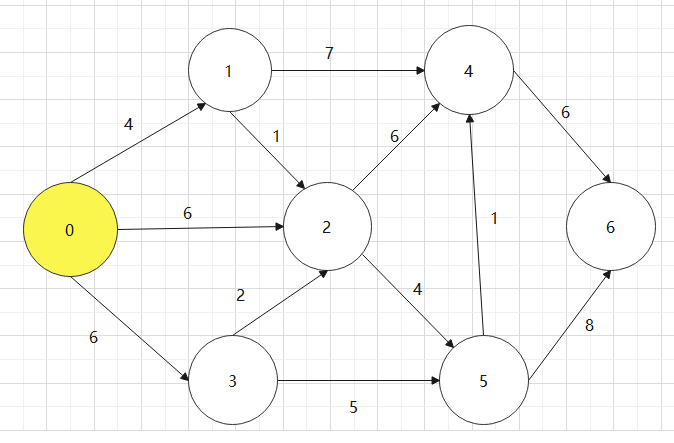
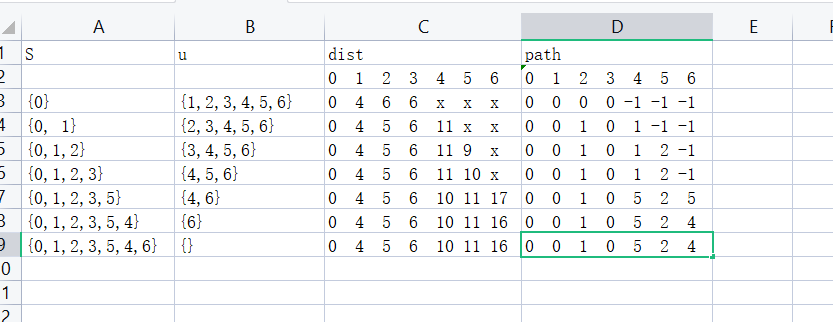
Dijkstra算法需要哪些辅助数据结构
数组s[]:选中的顶点
数组dist[]:源点到每个顶点的权值
数组path[]:存放源点v->j的最短路径上顶点j的前一个顶点编号
Dijkstra算法如何解决贪心算法无法求最优解问题？展示算法中解决的代码。
Dijkstra算法的时间复杂度，使用什么图结构，为什么。
时间复杂度：O（n^2)
不适合含有负权值的带权图求单源最短路径，因为该算法的第一个特性
1.4.2 Floyd算法求解最短路径
Floyd算法解决什么问题？
一种用于寻找给定的加权图中顶点间最短路径的算法（每对顶点之间的最短路径）
Floyd算法需要哪些辅助数据结构
二维数组A[][]:存放当前顶点之间的最短路径长度，即A[i][j]表示当前i->j的最短路径长度
二维数组path[][]:保存最短路径它与当前迭代的次数有关
- 代码
void Floyd(MatGraph g)
{
int A[MAXV][MAXV],path[MAXV][MAXV];
int i,j,k;
for(i=0;i<g.n;i++)
for(j=0;j<g.n;j++)
{ A[i][j]=g.edges[i][j];
if(i!=j&&g.edges[i][j]<INF)
path[i][j]=i;
else
path[i][j]=-1;
}
for(k=0;k<g.n;k++)
{
for(i=0;i<g.n;i++)
for(j=0;j<g.n;j++)
if(A[i][j]>A[i][j]+A[k][i])
{ A[i][j]=A[i][j]+A[k][i];//修改最短路径长度
path[i][j]=path[k][j];//修改最短路径
}
}
Dispath(g,A,path);
}
Floyd算法优势，举例说明。
1、是一种动态规划算法，稠密图效果最佳，边权可正可负（比Dijkstra算法有优势，应用范围较广）
2、于三重循环结构紧凑，对于稠密图，效率要高于Dijkstra算法，
3、与Dijkstra算法时间复杂度虽然相同，都为 O(n^3) ，但是弗洛伊德算法的实现形式更简单
最短路径算法还有其他算法，可以自行百度搜索，并和教材算法比较。
1.5 拓扑排序
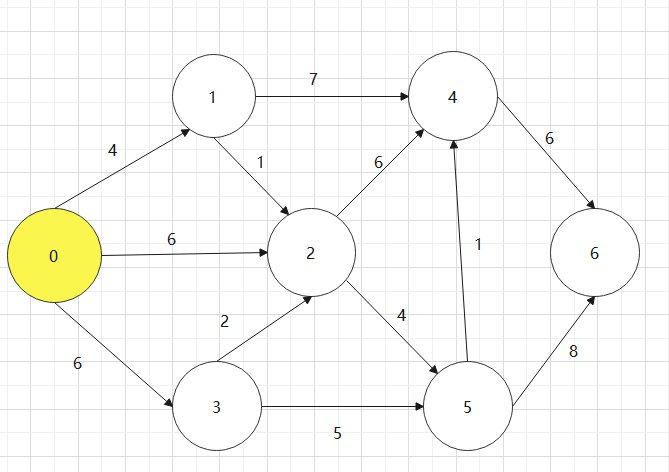
找一个有向图，并求其对要的拓扑排序序列
对于下图：0->1->4->3->2->5->6
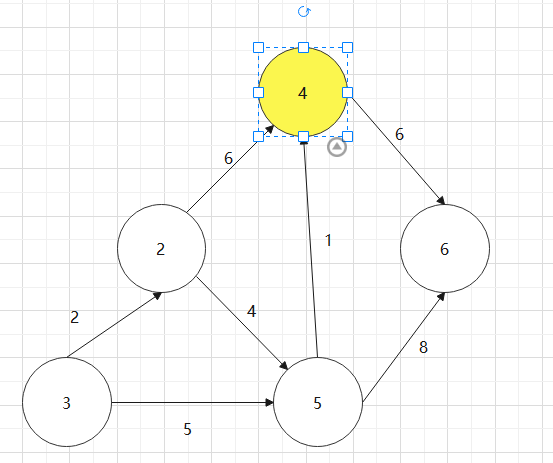
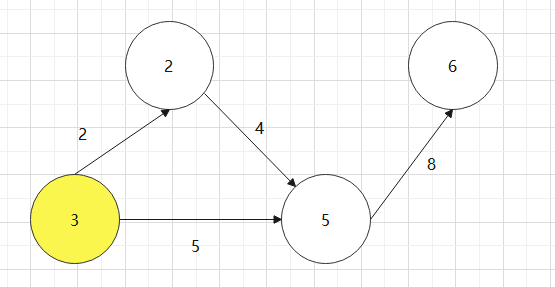
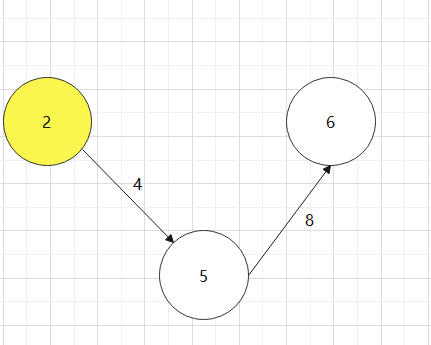
实现拓扑排序代码，结构体如何设计？
#define MAXV 20
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int info; //该边的相关信息，如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{
Vertex data; //顶点信息
int count; //入度
ArcNode *firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{ AdjList adjlist; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
书写拓扑排序伪代码，介绍拓扑排序如何删除入度为0的结点？
- 思路
1、比哪里邻接链表，计算每个结点的入度
2、利用for循环，将入度为0的结点入栈
3、利用while循环，当栈不为空时，出栈（访问），将栈顶元素i放入node数组，指针指向该结点（i）第一条边
4、利用while(p):访问顶点，入度减一，若此时有入度为0的结点，入栈，指针下移
5、若有环路（即访问顶点小于输入的顶点个数），输出error；否则利用for循环输出
- 伪代码
for i=0 to G->n-1 i++
更新p指针
while(p)
i顶点入度加一，更新指针p
end while
end for
for i=0 to G->n-1 i++
if i顶点的入度为0，入栈
end if
while 栈不空
取栈顶，访问顶点个数加一，更新指针p
while(p不为空）
访问ｐ指向的顶点，入度减一
若此时出现入度为０的点，将该点入栈，更新ｐ指针
ｅｎｄ ｗｈｉｌｅ
ｅｎｄ ｗｈｉｌｅ
如何用拓扑排序代码检查一个有向图是否有环路？
定义一个变量Tcount,计算拓扑排序被访问顶点个数，若Tcount<输入的顶点个数，则有环路，不能进行拓扑排序
1.6 关键路径
什么叫AOE-网？
- 定义：在带权有向图中，以顶点表示事件，有向边表示活动，边上的权值表示完成该活动的开销，则称这种有向图为用边表示活动的网络，简称为AOE网（Activity On Edge Network）
- 性质：
1、只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始
2、只有在进入某一顶点的各有向边所代表的活动都已经结束时，该顶点所代表的事件才发生
什么是关键路径概念？
从源点到汇点的所有路径中，具有最长路径长度的路径
什么是关键活动？
最长路径（关键路径）上的活动
2.PTA实验作业（4分）
2.1 六度空间（2分）
- 思路
1、利用邻接矩阵存储图结构，利用广度遍历计算两顶点间的距离
2、广度遍历函数：count计算两点间的距离，layer计算层，队列q
3、将每次要访问的点v入队，并标记v已访问，利用while(队不空时，并且层小于6时，出队；
利用for 若某一顶点i未被访问，并且该点i与v是相邻结点，结点间距加1，将i入队，标记i被访问，判断结点关系，计算layer++，更新变量结点
2.1.1 伪代码（贴代码，本题0分）
伪代码为思路总结，不是简单翻译代码。
while(q非空并且层数小于6时）
temp=队头元素，出队
for i=1 to n i++
if i未被访问到，并且i v两点是邻接点
then 层数加1，将i入队，标记i被访问，令end=i;
end if
end for
if last==temp
then 层数加1，last=end
end if
2.1.2 提交列表
2.1.3 本题知识点
利用广度遍历（广度遍历利用了队列）通过邻接矩阵来存储图结构，该题的图是一个稠密图
2.2 村村通或通信网络设计或旅游规划（2分）
2.2.1 伪代码（贴代码，本题0分）
伪代码为思路总结，不是简单翻译代码。
for i=1 to n i++
将lowcost[i]置初始值为edges[1][i]
closest[i]=1
end for
for i=1 to n-1 i++
初始化min为INF
for j=1 to n j++
if lowcost[j]!=0 lowcost[j]<min
then 将lowcost[j]复值给min k=j
end if
end for
num+=min
标记k已加入
for j=1 to n j++
if g.edges[k][j] != 0 && g.edges[k][j] < lowcost[j]
then 修正数组lowcost,closest
end if
end for
end for
2.2.2 提交列表
2.2.3 本题知识点
用到了prime算法，将最大值定义成INF
（PS：这个学期学的太难了！！！5555555特别时这个图和树的，真的学不会了。。。。这代码真的.........)
