中缀表达式转前后缀表达式的手工求法
无论是面试还是考研，数据结构中都会出现一类题型，就是已知中缀表达式求其前缀表达式或者后缀表达式。这类题型多遇见几个，多做几个掌握以下方法，就没问题了。
先说一个比较简单的，个人还是比较倾向于这种的二叉树表示法：
表达式A*B：左子树为表达式A，右子树为表达式B，可以先求左子树所表示的表达式的值，再求右子树所表示的表达式的值，最后二者相乘。注意，所画出的二叉树，它的叶子节点为数值，非叶子节点是运算符。画出二叉树以后，依次进行前序遍历和后序遍历，可以得出前缀表达式和后缀表达式。
例如美团曾经出过的一个笔试题目：
解答：
根据题目，我们可以画出二叉树，如图所示：
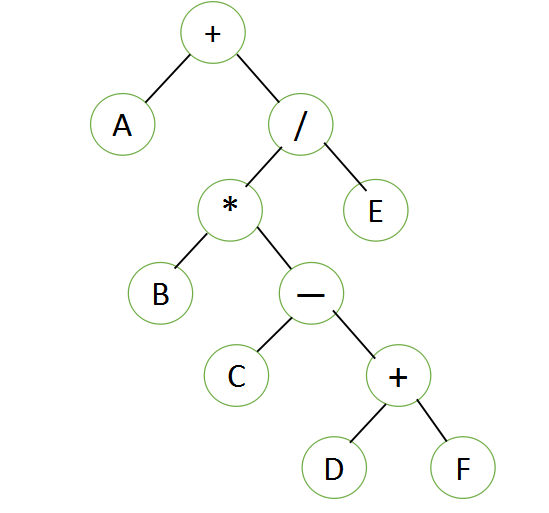
然后根据后序遍历，即可得出后缀表达式，前序遍历即可得出前缀表达式~
另外一种办法是利用栈进行操作，利用栈进行操作的这一种办法和许多书上不太一样，这是我在其他大牛的博客里学习的，那么在这里附上大牛写的博客的网址：
顺带把大牛总结的内容自己小结一下：
将中缀表达式转换为前缀表达式：
遵循以下步骤：
(1) 初始化两个栈：运算符栈S1和储存中间结果的栈S2；
(2) 从右至左扫描中缀表达式；
(3) 遇到操作数时，将其压入S2；
(4) 遇到运算符时，比较其与S1栈顶运算符的优先级：
(4-1) 如果S1为空，或栈顶运算符为右括号“)”，则直接将此运算符入栈；
(4-2) 否则，若优先级比栈顶运算符的较高或相等，也将运算符压入S1；
(4-3) 否则，将S1栈顶的运算符弹出并压入到S2中，再次转到(4-1)与S1中新的栈顶运算符相比较；
(5) 遇到括号时：
(5-1) 如果是右括号“)”，则直接压入S1；
(5-2) 如果是左括号“(”，则依次弹出S1栈顶的运算符，并压入S2，直到遇到右括号为止，此时将这一对括号丢弃；
(6) 重复步骤(2)至(5)，直到表达式的最左边；
(7) 将S1中剩余的运算符依次弹出并压入S2；
(8) 依次弹出S2中的元素并输出，结果即为中缀表达式对应的前缀表达式。
将中缀表达式转换为后缀表达式：
与转换为前缀表达式相似，遵循以下步骤：
(1) 初始化两个栈：运算符栈S1和储存中间结果的栈S2；
(2) 从左至右扫描中缀表达式；
(3) 遇到操作数时，将其压入S2；
(4) 遇到运算符时，比较其与S1栈顶运算符的优先级：
(4-1) 如果S1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
(4-2) 否则，若优先级比栈顶运算符的高，也将运算符压入S1（注意转换为前缀表达式时是优先级较高或相同，而这里则不包括相同的情况）；
(4-3) 否则，将S1栈顶的运算符弹出并压入到S2中，再次转到(4-1)与S1中新的栈顶运算符相比较；
(5) 遇到括号时：
(5-1) 如果是左括号“(”，则直接压入S1；
(5-2) 如果是右括号“)”，则依次弹出S1栈顶的运算符，并压入S2，直到遇到左括号为止，此时将这一对括号丢弃；
(6) 重复步骤(2)至(5)，直到表达式的最右边；
(7) 将S1中剩余的运算符依次弹出并压入S2；
(8) 依次弹出S2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式（转换为前缀表达式时不 用逆序）。
综上所述，对于出现这种已知中缀表达式求前缀表达式和后缀表达式的话，优先采用二叉树，选择而已，不用花费太长的时间。
不足之处：后期有时间考虑加上代码~
