红黑树（二）

删除

首先，搜索要删除的节点。

情况一：如果该节点左子节点是nil，删除后让右子节点顶替该节点的位置即可。

情况二：如果该节点右子节点是nil，删除后让左子节点顶替该节点的位置即可。

情况三：如果该节点左右节点都不为nil，则查询其后继节点，即右节点中最小的节点，让其顶替该节点，颜色设置为被删除节点的颜色，因为这样可以满足，该节点大于左侧子树中的所有节点，小于右侧子树中的所有节点。顶替节点从原来位置删除，因为该节点是右侧子树中最小的节点，所以该节点一定没有左子节点，如此让右子节点顶替该节点的位置即可。

来看看一系列操作下来，有那些性质被破坏了。如果一二种情况中删除节点是黑色，或者第三种情况替换节点的本来颜色是黑色，那么相当于有一层的黑色被去掉了，那么肯定不满足性质5

还有就是如果一二种情况中删除节点后顶替上来的是红色节点，而删除节点父节点同样也是红色节点，这种情况下删除节点的颜色一定是黑色，或者第三种情况顶替节点原来位置顶替上来的节点是红色，而父节点是红色，这种情况下顶替节点的原来颜色一定是黑色，这两种情况就违背了性质4。

如果是一二种情况删除的是根节点，顶替上来节点是红色，则违背了性质2.

针对性质2，在所有性质都恢复后，将根节点设置为黑色即可，高操作不会影响其他任何性质。

这对性质4，将可以将一二种情况下的顶替节点或者第三种情况下占有顶替节点原来位置的节点设置为黑色即可满足性质4。

针对性质5，可以将一二种情况下的顶替节点或者第三种情况下占有顶替节点原来位置的节点看作有一层额外颜色-黑色。如此可满足性质5，但是这种方法出现了一个问题，那就是同意节点有两种颜色，违背了性质1。性质1通过一些操作即可恢复。

 

当性质4满足，性质5（转化为性质1）不满足的时候，那么节点x一定是黑色。做何种操作才能恢复性质1呢。

节点x为上述情况一、二中顶替节点，情况三中占有顶替节点的节点。即顶替节点原来位置的右子节点。

针对下面4种情况进行操作。

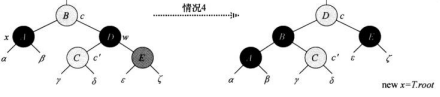
情况一：x节点的兄弟节点为红色。那么变换颜色并左旋，让x的兄弟节点便称黑色，转化为情况二、三、四。

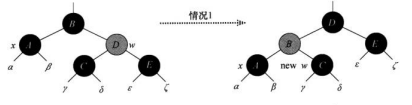
情况二：x节点的兄弟节点为黑色，且兄弟节点的两个子节点是黑色。那么提出一层黑色，传递给父节点。将父节点设置为x。情况二是可能循环的情况，因为他是将额外颜色上提。并没有处理性质1。

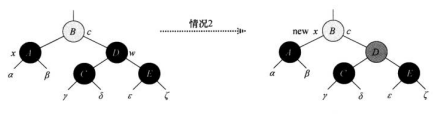
情况三：x节点的兄弟节点是黑色，兄弟节点的左孩子是红色的，兄弟节点的右孩子是黑色。改变颜色并以w为中心右旋，让w右孩子是红色，转化为情况四。

 

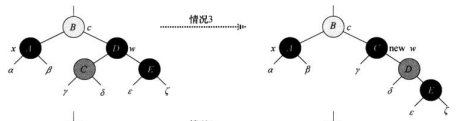
情况四：x节点的兄弟节点是黑色，兄弟节点的右孩子是红色，改变颜色并左旋，然后就可以让多出来的黑色节点顶替额外的黑色。让其满足性质1。结束循环。