全排列(递归)

排列：

从n个数中选取m（m<=n）个数按照一定的顺序进行排成一个列，叫作从n个元素中取m个元素的一个排列。不同的顺序是一个不同的排列。从n个元素中取m个元素的所有排列的个数，称为排列数。

全排列：

从n个元素取出n个元素的一个排列，称为一个全排列。全排列的排列数公式为

时间复杂度：

n个数的全排列有n!种，每一个排列都有n个数据，所以输出的时间复杂度为O(n*n!)，呈指数级，无法处理大型数据。

题目要求

输入：_permute('abc')

输出：['abc','acb','bac','bca','cab','cba']

思路分析

全排列的解决方法有很多种，递归，回溯，暴力等。我这里使用的是回溯法。
所谓回溯法，就是在程序执行结束之后又返回到之前遍历的地方继续下一次遍历

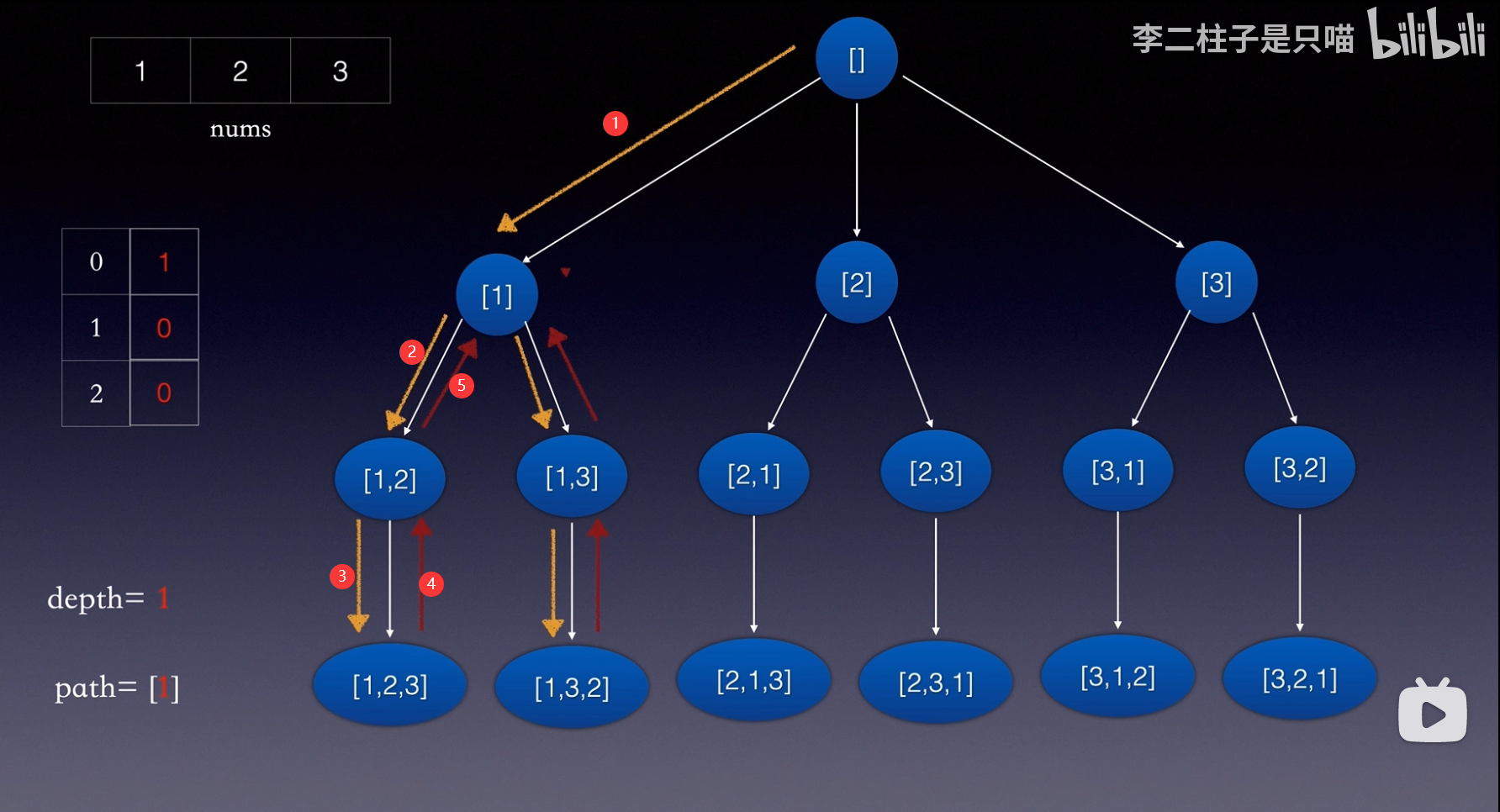
参考B站up主：李二柱子是只喵
需要注意一次遍历到底侯需要回溯

代码示例

const permute = (nums) => {
  // 一次的数据　
  const path = []
  // 所有的结果
  const res = []
  // 该位置的数字之前是否访问过，默认为0表示未访问过
  let use = new Array(nums.length).fill(0)
  // 遍历的深度
  let depth = 0

  // dfs(nums, depth, use, path, res)
  const dfs = () => {
    // 递归退出条件，如果深度等于数组长度，则说明已经遍历到树的叶子节点
    if (depth === nums.length) {
      res.push([...path])
      return
    }
    // 遍历数组
    for (let i = 0; i < nums.length; i++) {
      // 判断当前元素是否使用过，如果用过则跳出
      if (use[i]) {
        continue
      }
      path.push(nums[i])
      depth++
      use[i] = 1
      dfs(nums, depth, use, path, res)
      use[i] = 0
      depth--
      path.pop()
    }
  }
  dfs()
  return res

}
console.log(permute([1, 2, 3, 4]))