动态规划
动态规划
常见题型:
- 最小编辑距离
- 最长回文子序列
- 斐波那契数列
- 零钱兑换问题
动态规划特点
- 重叠子问题
- 状态转移方程(关键)
- 最优子结构
题型: 求最值
核心: 穷举
解题套路
- 明确[状态]
- 明确[选择]
- 明确 dp 函数/数组的定义
- 明确 base case
斐波那契数列
一般的解题都是调用递归,递归的算法复杂度计算方法是:函数本身复杂度乘以递归深度。
如果我们采用递归的方式去解题就会发现存在着很多的冗余操作,比如计算当 n=20 时的值,那么递归就会调用 f(19)+f(18),在 f(19)种会计算 f(17),在 f(18)中同样也会计算 f(17),会比较冗余。因此我们可以采用记事本的方法,通俗点来说就是将每次的结果进行记录,下次再调用之前先去判断,如果有记录就直接使用,没有的话才递归。
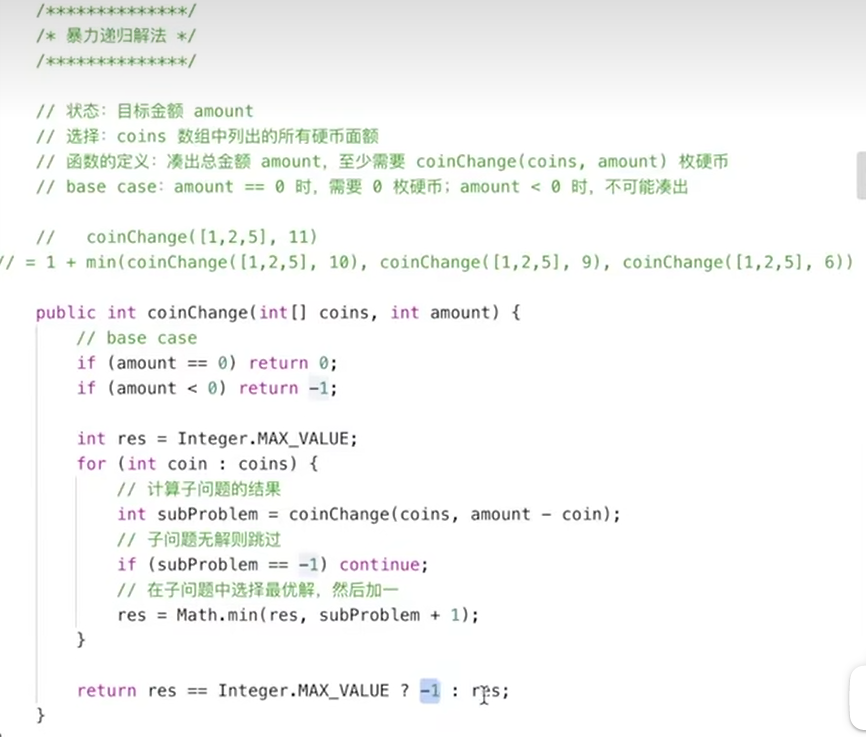
暴力递归解法

带备忘录的递归解法
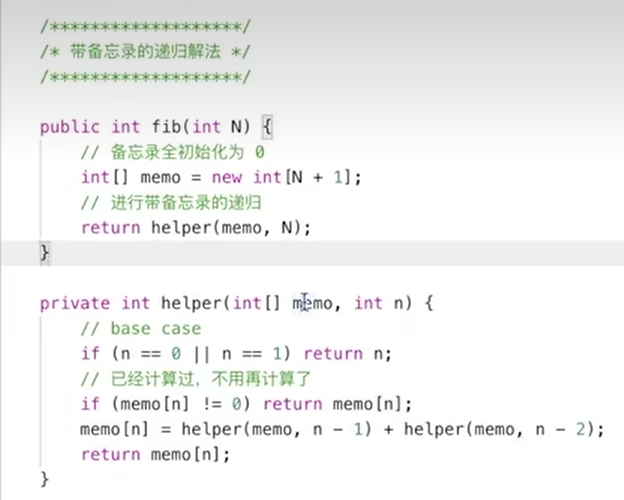
优化空间复杂度
空间换时间

零钱兑换
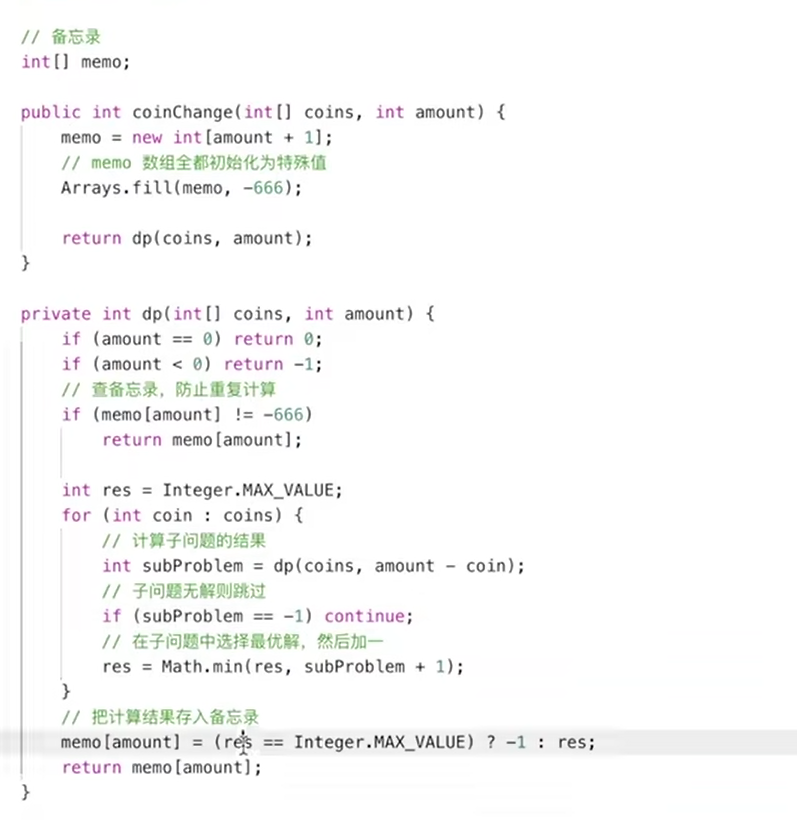
带备忘录的解法

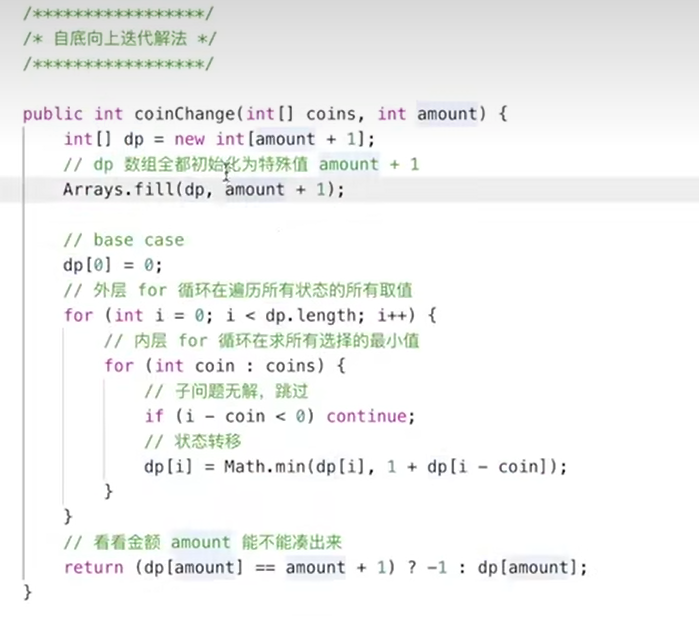


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 25岁的心里话
· 闲置电脑爆改个人服务器(超详细) #公网映射 #Vmware虚拟网络编辑器
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 零经验选手,Compose 一天开发一款小游戏!
· 一起来玩mcp_server_sqlite,让AI帮你做增删改查!!