力扣 题目84- 柱状图中最大的矩形

题目

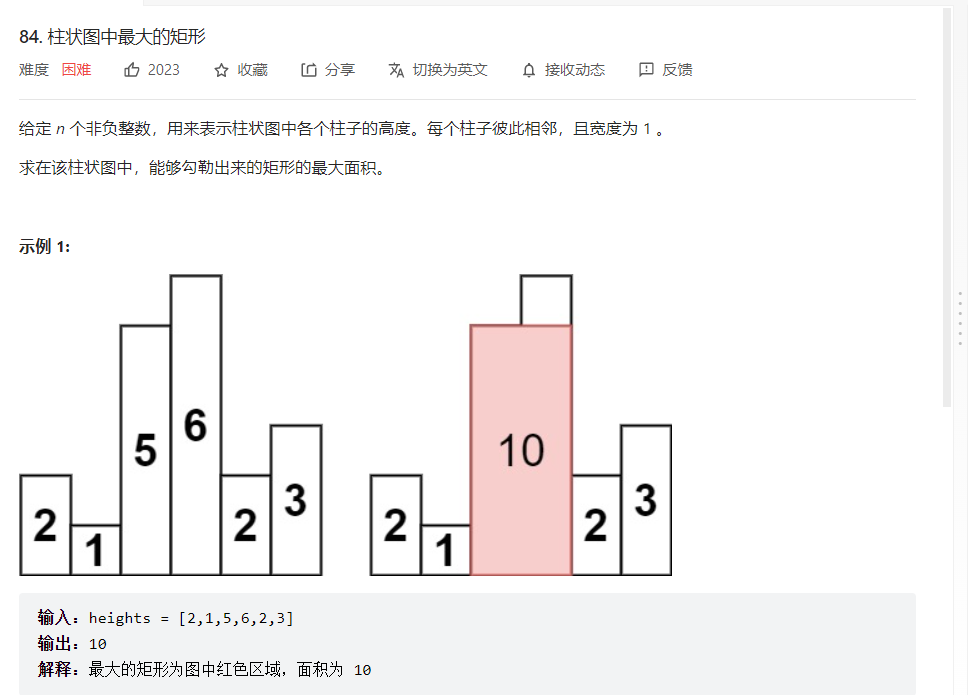
题解

这题其实如果不考虑时间 穷举应该挺容易想到的 即

找到向左找到第一个高度小于当前柱体 i 的柱体，向右找到第一个高度小于当前柱体 i 的柱体。

每个柱子我们都如上计算一遍以当前柱子作为高的矩形面积，最终比较出最大的矩形面积即可。(这里用循环比较)

但是这样力扣肯定不会让我们过的

那么在如何找左小和右小的地方需要进行修改

我们发现在遍历的过程中

1.进行和上一个柱体的高度比较 如果当前遍历的柱体比上一个柱体短 那么上一个柱体的右小就是当前遍历的柱体

2.如果我们用一个容器去存储增大时候的状况 那么被存储的柱体的前一个就是被存储的柱体的左小

知道了上面两点 我们发现这个容器选择 栈不错 

但是问题来了 我们只看6的情况下 5与2 此时面积为6 是可以用上面两行解释的(按照1的逻辑 此时应该遍历到2)

但是5的情况下 应该是1与2  该怎么办呢 有了!我们在对6执行完毕的时候 出栈 这样5就成为了栈顶 也就是说 当前柱体由6改为5  此时遍历的仍然是2(比较栈顶)即右小 而5的上一个是1依然是左小

这样遍历就一清二楚了 而最大的难道就是计算面积时不再采用以柱子顺序计算 与平常思想有点违背 所以这题的思维很重要

            while (stack.size()!=0 && heights[i] < heights[stack.top()]) {
                int h = heights[stack.top()];
                //出栈 进行上一个柱体的操作
                stack.pop();
                area = max(area, (i - stack.top() - 1) * h);
            }
            stack.push(i);

 

代码

#include <iostream>
#include<vector>
#include<stack>
using namespace std;
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        heights.insert(heights.begin(),0);
        heights.push_back(0);
        stack<int> stack;
        int area = 0;
        //0 1
        for (int i = 0; i < heights.size(); i++) {
            // 对栈中柱体来说，栈中的下一个柱体就是其「左边第一个小于自身的柱体」；
            // 若当前柱体 i 的高度小于栈顶柱体的高度，说明 i 是栈顶柱体的「右边第一个小于栈顶柱体的柱体」。
            // 因此以栈顶柱体为高的矩形的左右宽度边界就确定了，可以计算面积
            while (stack.size()!=0 && heights[i] < heights[stack.top()]) {
                int h = heights[stack.top()];
                //出栈 进行上一个柱体的操作
                stack.pop();
                area = max(area, (i - stack.top() - 1) * h);
            }
            stack.push(i);
        }

        return area;
    }
};
int main() {
    vector<int> height = { 2,1,5,6,2,3 };
    Solution sol;
    int max = sol.largestRectangleArea(height);
    cout << max << endl;

}