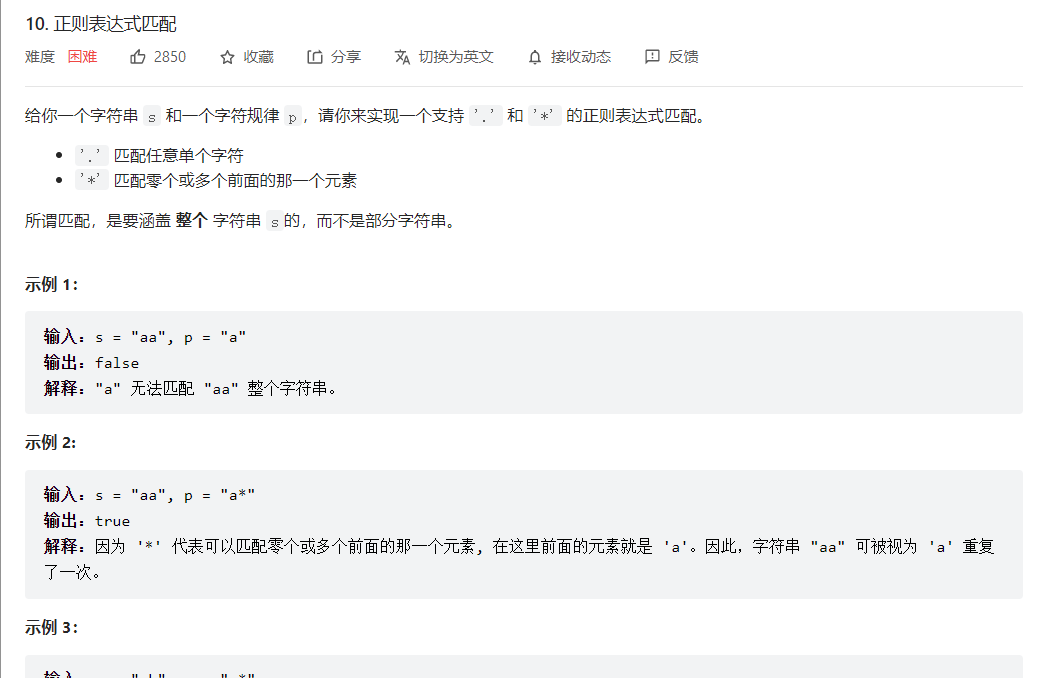
题目
题解
没做出来呜呜呜只能看别人写的题解了 题解看这里
参考题解
作者:zhang-jian-qi-shi
链接:https://leetcode-cn.com/problems/regular-expression-matching/solution/c-dong-tai-gui-hua-by-zhang-jian-qi-shi-rzyp/
来源:力扣(LeetCode)
好在经过上一篇之后 这篇题解也能很快的看懂了
这里我再解析一点 能够看的更懂(反正是给我自己看 如果有大佬看到有什么不对的地方还是请谅解小白)
当p[j-1]=='*',
可以不匹配
dp[i][j]=dp[i][j-2]
拿个例子来说
abc
a*bc
这里的*就是不匹配 因为有0个匹配项 所以直接忽略这个* 以此j要j-2拿到*之前的那个字符a
因此dp[1][2]=dp[1][0]
可以匹配多次
当匹配为 1 个:dp[i][j]=dp[i-1][j-2] && (s[i-1] == p[j - 2] || p[j - 2] == '.')
拿个例子来说
aabc
a*bc
首先你要确保之前的匹配成功即dp[i-1][j-2]
然后s[i-1] == p[j - 2]->j - 2 *前面的那个字符 和现在s的i-1字符比较
.就是可以任意匹配
aaabc
a*bc
当匹配为 2 个:dp[i][j]=dp[i-2][j-2] && (s[i-2] == p[j - 2] &&s[i-1] == p[j - 2] || p[j - 2] == '.')
首先你要确保之前*之前的匹配成功即dp[i-2][j-2] 因为此时i又增加了1所以这次减2
然后s[i-2] == p[j - 2] &&s[i-1] == p[j - 2] 即*前面的那个字符 和现在s的i-1和i-2 两个字符比较(因为匹配为 2 个)
.就是可以任意匹配
然后就可以推第三个 第四个...
所以第i个就是
dp[i][j]=dp[i][j-2]||(dp[i-1][j-2] && (s[i-1] == p[j - 2] || p[j - 2] == '.'))||(dp[i-2][j-2] && (s[i-2] == p[j - 2] &&s[i-1] == p[j - 2] || p[j - 2] == '.'))||...
然后i-1个是
dp[i-1][j]=dp[i-1][j-2]||(dp[i-2][j-2] && (s[i-2] == p[j - 2] || p[j - 2] == '.'))||(dp[i-3][j-2] && (s[i-3] == p[j - 2] &&s[i-2] == p[j - 2] || p[j - 2] == '.'))||...
直接把i-1的代入i的
dp[i][j]=dp[i][j-2]||dp[i-1][j]&&(s[i-1]==p[j-2]||p[j-2]=='.')
这样结果就出来了
要注意
s一个字符都不选,此时要考虑p包含*的情况,因为*可以不匹配。
for(int i=2;i<=n;i++){
if(p[i-1]=='*')
dp[0][i]=dp[0][i-2];
}
代码
作者:zhang-jian-qi-shi
链接:https://leetcode-cn.com/problems/regular-expression-matching/solution/c-dong-tai-gui-hua-by-zhang-jian-qi-shi-rzyp/
来源:力扣(LeetCode)
#include<iostream>
#include<string>
#include <vector>
using namespace std;
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size(), n = p.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, false));//类似于二维数组
dp[0][0] = true;
for (int i = 2; i <= n; i++) {
if (p[i - 1] == '*')
dp[0][i] = dp[0][i - 2];
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (p[j - 1] == '*') {
dp[i][j] = dp[i][j - 2] || (dp[i - 1][j] && (s[i - 1] == p[j - 2] || p[j - 2] == '.'));
}
else {
dp[i][j] = dp[i - 1][j - 1] && (s[i - 1] == p[j - 1] || p[j - 1] == '.');
}
}
}
return dp[m][n];
}
};
int main() {
Solution sol;
bool zheng=sol.isMatch("aaa","a*");
cout << zheng << endl;
}



