树、二叉树、查找算法总结
一、思维导图

二、重要概念笔记
1、树的基本术语
- 树是n个结点的有限集。
- 树的结点包含一个数据元素及若干个指向其子树的分支。
- 结点拥有的子树数称为结点的度。
- 度为0的结点称为叶子或者终端结点。
- 度不为0的结点称为非终端结点或分支结点。
- 除根结点之外,分支结点也称为内部结点。
- 结点的子树称为该结点的孩子,相应地,该结点称为孩子的双亲。
- 同一个双亲的孩子之间互称兄弟。
- 如果将树中的结点的各子树看成从左到右是有次序的,则称该树为有序树,否则称为无序树。
- 森林是m(m>=0)棵互不相交的树的集合。
2、树的性质
- 树中的结点数等于所有结点的度数之和加一
- 度为m的树中第i层上最多有m的i-1次方个结点(i>=1)
- 高度为h的m次树最多有(m^h-1)/(m-1)个结点
- 具有n个结点的m次树的最小高度为[logm^(n(m-1)+1)]
3、二叉树的性质
- 非空二叉树上的叶子的结点数等于双分支结点数加1
- 非空二叉树的第i层上最多有2^(i-1)个结点.
- 高度为h的二叉树最多有2^h-1个结点
- 具有n个结点的完全二叉树的高度为[log(n+1)]或[logn]+1
4、二叉树的遍历
- 先序遍历————根-左-右
- 中序遍历————左-根-右
- 后序遍历————左-右-根
- 层序遍历————根-逐层从左到右
5、平衡二叉树中插入结点失衡的调整
1、LL型调整
由于在A左子树根结点的左子树上插入结点C,A的平衡因子由1增至2,致使以A为根的子树失去平衡,则需要进行一次向右的顺时针旋转操作,如下图所示。
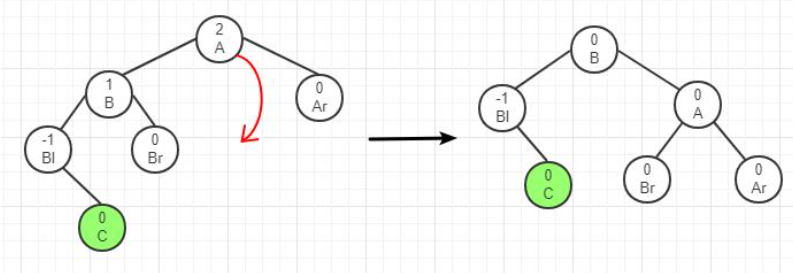
2、RR型调整
由于在A的右子树根结点的右子树上插入结点C,A的平衡因子由-1变为-2,致使以A为根结点的子树失去平衡,则需进行一次向左的逆时针旋转操作,如下图所示。

3、LR型调整
由于在A的左子树根结点的右子树上插入结点,A的平衡因子由1增至2,致使以A为根结点的子树失去平衡,则需要进行二次旋转操作。第一次对B及其右子树进行逆时针旋转,C转上去成为B的根,这时变成了LL型,所以第二次进行LL型的顺时针旋转即可恢复平衡。如果C原来有左子树,则调整C的左子树为B的右子树,如下图所示。
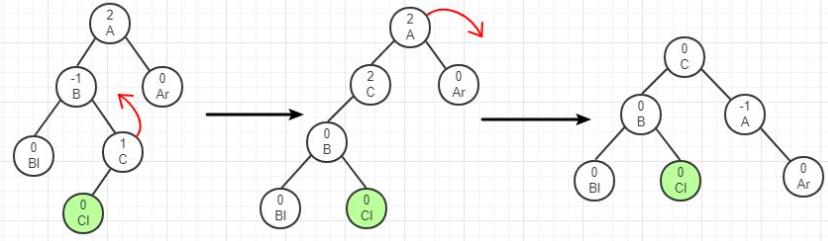
4、RL型调整
由于在A的右子树根结点的左子树上插入结点,A的平衡因子由-1变为-2,致使以A为根结点的子树失去平衡,则旋转方法和LR型相对称,也需进行两次旋转,第一次对B及其左子树进行顺时针右旋,C转上去成为B的根,这时变成了RR型,再进行RR型的逆时针左旋,如下图所示。

6、m阶B_树的特性
- 定义任意非叶子结点最多只有M个儿子,且M>2;
- 根结点的儿子数为[2, M];
- 除根结点以外的非叶子结点的儿子数为[M/2, M],向上取整;
- 非叶子结点的关键字个数=儿子数-1;
- 所有叶子结点位于同一层;
7、m阶B+树的特性
- 有n棵子树的非叶子结点中含有n个关键字(b树是n-1个),这些关键字不保存数据,只用来索引,所有数据都保存在叶子节点(b树是每个关键字都保存数据)。
- 所有的叶子结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
- 所有的非叶子结点可以看成是索引部分,结点中仅含其子树中的最大(或最小)关键字。
- 通常在b+树上有两个头指针,一个指向根结点,一个指向关键字最小的叶子结点。
- 同一个数字会在不同节点中重复出现,根节点的最大元素就是b+树的最大元素。
三、疑难问题及解决方案
- 对二叉排序树的删除操作编写代码时,对于既有左孩子又有右孩子的结点代码逻辑理解很模糊不清,无法实现函数代码编写
- 解决方案:
void DeleteBST(TreeNodeP &T, int key)
{
if (T == NULL)
{
return;
}
else
{
if (key > T->data)
{
DeleteBST(T->rchild, key);
}
else if (key < T->data)
{
DeleteBST(T->lchild, key);
}
else
{
Delete(T);
return;
}
}
}
void Delete(TreeNodeP &T)
{
TreeNodeP q = T;
if (T->lchild == NULL)
{
q = T;
T = T->rchild;
free(q);
}
else if (T->rchild == NULL)
{
q = T;
T = T->lchild;
free(q);
}
else
{
Deletel(T, T->lchild);
}
}
void Deletel(TreeNodeP& T, TreeNodeP& p)
{
TreeNodeP q;
if (p->rchild != NULL)
{
Deletel(T, p->rchild);
}
else
{
T->data = p->data;
q = p;
p = p->lchild;
free(q);
}
}



