C++Boost实现A*启发式算法搜索最小路径

参考链接1：https://www.cnblogs.com/xiaochi/p/8671740.html

参考链接2：http://www.mamicode.com/info-detail-2486552.html

在宽度优先和深度优先搜索里面，我们都是根据搜索的顺序依次进行搜索，可以称为盲目搜索，搜索效率非常低。

而启发式搜索则大大提高了搜索效率，由这两张图可以看出它们的差别：

 

 

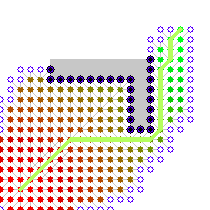
（左图类似与盲搜，右图为启发式搜索）

 

很明显启发式的搜索效率远远大于盲搜。

什么是启发式搜索（heuristic  search）

　　利用当前与问题有关的信息作为启发式信息，这些信息是能够提升查找效率以及减少查找次数的。

如何使用这些信息，我们定义了一个估价函数 h(x) 。h(x)是对当前状态x的一个估计，表示 x状态到目标状态的距离。

有：1、h(x) >= 0 ；  2、h(x)越小表示 x 越接近目标状态； 3、如果 h(x) ==0 ，说明达到目标状态。

与问题相关的启发式信息都被计算为一定的 h(x) 的值，引入到搜索过程中。

　　然而，有了启发式信息还不行，还需要起始状态到 x 状态所花的代价，我们称为 g(x) 。比如在走迷宫问题、八数码问题，我们的 g(x) 就是从起点到 x 位置花的步数 ，h(x) 就是与目标状态的曼哈顿距离或者相差的数目；在最短路径中，我们的 g(x) 就是到 x 点的权值，h(x)  就是 x 点到目标结点的最短路或直线距离。

　　现在，从 h(x) 和 g(x) 的定义中不能看出，假如我们搜索依据为 F(x) 函数。

　　当 F(x) = g(x) 的时候就是一个等代价搜索，完全是按照花了多少代价去搜索。比如 bfs，我们每次都是从离得近的层开始搜索，一层一层搜 ；以及dijkstra算法，也是依据每条边的代价开始选择搜索方向。 

　　当F(x) = h(x) 的时候就相当于一个贪婪优先搜索。每次都是向最靠近目标的状态靠近。

　　人们发现，等代价搜索虽然具有完备性，能找到最优解，但是效率太低。贪婪优先搜索不具有完备性，不一定能找到解，最坏的情况下类似于dfs。

　　这时候，有人提出了A算法。令F(x) = g(x) + h(x) 。（这里的 h(x) 没有限制）。虽然提高了算法效率，但是不能保证找到最优解，不适合的 h(x)定义会导致算法找不到解。不具有完备性和最优性。

　　几年后有人提出了 A*算法。该算法仅仅对A算法进行了小小的修改。并证明了当估价函数满足一定条件，算法一定能找到最优解。估价函数满足一定条件的算法称为A*算法。它的限制条件是 F(x) = g(x) + h(x) 。 代价函数g(x) >0 ；h(x) 的值不大于x到目标的实际代价 h*(x) 。即定义的 h(x) 是可纳的，是乐观的。

 

         不同的估价函数对算法的效率可能产生极大的影响。尤其是 h(x) 的选定，比如在接下来的八数码问题中，我们选择了曼哈顿距离之和作为 h(x) ，你也可以选择相差的格子作为 h(x)，只不过搜索的次数会不同。当 h(x) 越接近 h*(x) ，那么扩展的结点越少！

 

用boost的图论库编辑代码如下：

#include <iostream>
#include <string>
#include <utility>
#include <vector>
#include <deque>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/astar_search.hpp>//A*寻路算法
using namespace std;
using namespace boost;

enum { A, B, C, D, E, N };
string Names = "ABCDE";
//定义别名,两个顶点直接连接的边
using Edge = pair<int, int>;
//创建一个图                 边     顶点    有方向   无特性            边的权重是int
using Graph = adjacency_list<listS, vecS, directedS, no_property, property<edge_weight_t, int>>;
//创建一个图
Graph make_graph()
{
    //连接的边
    vector<Edge> edges = { {A,B}, {A,C},{A,D},{B,E},{C,E},{D,E} };
    //边对应的权重
    vector<int> weight = { 3,1,4,5,2,6 };
    //创建一个图对象
    return Graph(edges.begin(), edges.end(), weight.begin(), N);
}
//创建一个结构体,用于抛出找到信息
struct found_goal
{

};
//A*要到达的目标顶点
template<class vertex>
class astar_my_visitor :public boost::default_astar_visitor
{
public:
    //初始化内置地图
    astar_my_visitor(vertex goal) :m_goal(goal)
    {

    }
    //重载examine_vertex方法
    template<class Graph>
    void examine_vertex(vertex v, Graph &g)
    {
        //如果与目标顶点一样,则说明找到
        if (v == m_goal)
        {
            //抛出抛出找到信息
            throw found_goal();
        }
    }
private:
    //目标顶点
    vertex m_goal;
};

//计算权重寻找最短路径
template<class Graph,class costtype>
class distance_heuristic :public boost::astar_heuristic<Graph, costtype>
{
public:
    //类型替换
    using Vertex = typename boost::graph_traits<Graph>::vertex_descriptor;
    //初始化
    distance_heuristic(Vertex Goal, Graph &graph):Goal_(Goal),graph_(graph)
    {
    }
    //重载()运算符 获得目标点到指定点的距离
    costtype operator()(Vertex v)
    {
        return get(vertex_index, graph_, Goal_) - get(vertex_index, graph_, v);
    }
private:
    Vertex Goal_;
    Graph &graph_;
};


int main()
{
    //创建图
    Graph myg = make_graph();

    //创建简写
    using Vertex = boost::graph_traits<Graph>::vertex_descriptor;
    using Cost = int;

    Vertex start = vertex(A, myg);//开始位置
    Vertex goal = vertex(E, myg);//结束位置

     //保存走过路径(由后向前)
    vector<Vertex>parents(boost::num_vertices(myg));
    //保存长度
    vector<Cost>distance(boost::num_vertices(myg));

    try
    {
        //求从指定点到终点的路线
        boost::astar_search_tree(myg, start, distance_heuristic<Graph, Cost>(goal, myg),//传递距离
           //求出路径，以及路径对应的权重，访问器访问                                 因为重载了()运算符
            boost::predecessor_map(&parents[0]).distance_map(&distance[0]).visitor(astar_my_visitor<Vertex>(goal))
        );
    }
    //catch信息
    catch (found_goal fg)
    {
        //要到的位置的前一个到达的位置如果是goal(下标是当前点,值是到这个点之前的点)
        if (parents[goal] == goal)
        {
            cout << "无路可走" << endl;
        }
        deque<Vertex> route;
        //顺藤摸瓜
        for (Vertex v = goal; v != start; v = parents[v])
        {
            route.push_front(v);
        }
        cout<<"从"<<Names[start]<<"到"<<Names[goal]<<"的最短路径为："<<endl;
        cout << Names[start];
        for (auto i : route)
        {
            cout <<"->"<< Names[i];
        }
        cout<<endl;
    }
    return 0;
}

运行结果如图