坐标系与参数方程

注：以下内容来源于https://wenku.baidu.com/view/a44869e1f424ccbff121dd36a32d7375a417c6c9.html，感谢分享！

一、坐标系

    1、平面直角坐标系中的伸缩变换

          设点P(x,y)是平面直角坐标系xOy中的任意一点，在变换

 

 

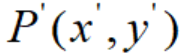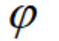 的作用下，点P(x,y)对应到点，我们把称为平面直角坐标系xOy中的坐标伸缩变换，简称伸缩变换。

 

 

 

    2、极坐标系

       （1）极坐标系的概念

                如图所示，在平面内取一个定点O，叫做极点；自极点O引一条射线Ox，叫做极轴；再选定一个长度单位，一个角度单位（通常取弧度）及其正方向（通常取逆时针方向），这样我们就建立了一个极坐标系。

 

 

      （2）极坐标

             设点M是平面内一点，极点O与点M的距离叫做点M的极径，记为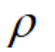；以极轴Ox为始边，射线OM为终边的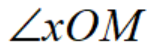叫做点M的极角，记为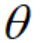。我们把有序对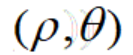叫做点M的极坐标，记为。

 

 

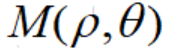       （3）极径、极角的取值范围

                 一般地，极径，极角。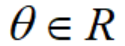

    3、极坐标与直角坐标之间的互化

         如图所示，设点M是平面内任意一点，记点M的直角坐标为（x,y），极坐标为 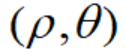。我们可以得到极坐标与直角坐标之间如下关系：

 

 

 

       （i）直角坐标化极坐标：

                                        

         (ii)极坐标化直角坐标

                                    

 

 

 

 

 

 

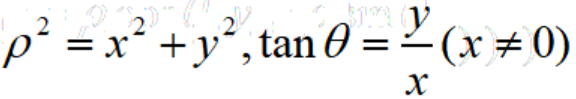
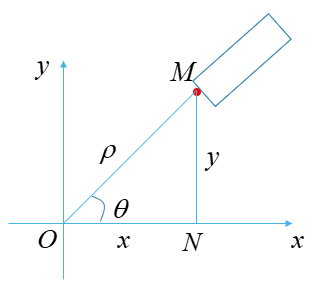
 【注】上面两类关系式是我们进行极坐标与直角坐标互化的重要关系式。解题时，大家要根据题意灵活选用。

    4、几个简单曲线的极坐标方程

        （1）圆的极坐标方程：圆心在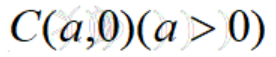，半径为a的圆的极坐标方程为；

 

 

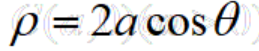          （2）直线的极坐标方程：经过极点，从极轴到直线的角是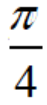的直线l的极坐标方程为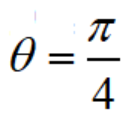和。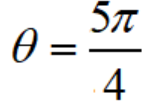

    5、柱坐标系与球坐标系

        (1)柱坐标系

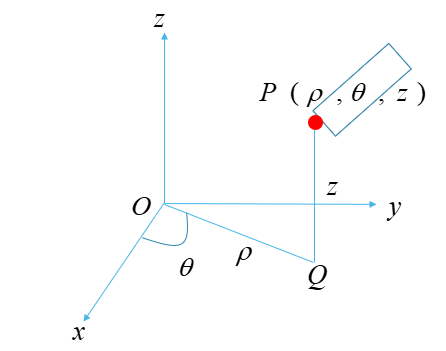
             如图所示，建立空间直角坐标系Oxyz，设点P是空间中任意一点，它在Oxy平面上的射影点为Q，用 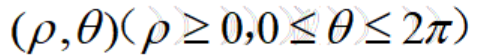表示点Q在Oxy平面上的极坐标，这时点P的位置可用有序数组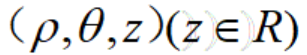

 

 

 表示。我们把建立上述对应关系的坐标系叫做柱坐标系；相应地，把有序数组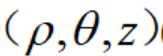叫做点P的柱坐标，记作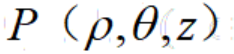

 

 

 ,其中，，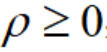

 

 

。

 

 

 

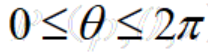 【注】直角坐标与柱坐标互化的变换公式：

         （2）球坐标系 

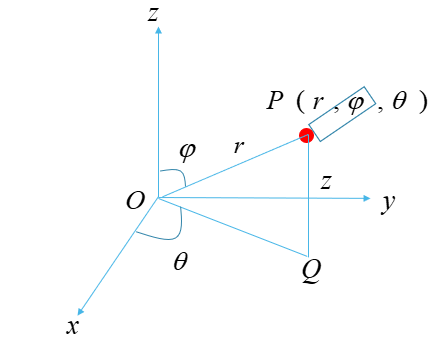
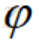                   如图所示，建立空间直角坐标系Oxyz，设点P是空间中任意一点，连结OP，记，OP与Oz轴正向所夹的角为，设点P在Oxy平面上的射影为点Q，Ox轴按逆时针方向旋转到OQ时所转过的正角为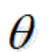，这样点P的位置就可以用有序数组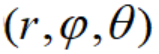表示。我们把建立上述对应关系的坐标系叫做球坐标系（或空间极坐标系）；相应地，把有序数组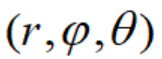叫做点P的球坐标，记作，其中

 

，

 

 

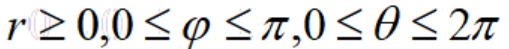
   【注】直角坐标与球坐标互化的变换公式：

二、参数方程

    1、参数方程的概念

         一般地，在平面直角坐标系中，如果曲线上任意一点的坐标x,y都是某个变数t的函数

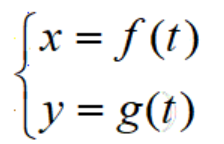
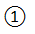，并且对于t的每一个允许值，由方程组所确定的点P(x，y)都在这条曲线上，那么我们就把方程组

 

 叫做这条曲线的参数方程，而把联系变数x，y的变数t叫做参变数，简称参数。

    2、参数方程与普通方程之间的互化

          曲线的参数方程与普通方程是曲线方程的两种不同形式。一般地，可以通过消去参数，由参数方程得到普通方程；反之，如果已知变数x，y中的一个与参数t的关系，例如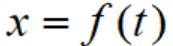，则我们可以通过把它带入普通方程，求出另一个变数与参数的关系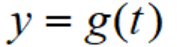，由此得到的方程组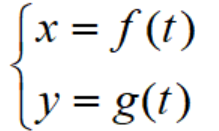就是该曲线的参数方程。

 

 

   【注】在解决参数方程与普通方程互化的问题时，必须要使x,y的取值范围保持一致。

    3、几个简单曲线的参数方程

        （1）圆的参数方程：圆心在原点O，半径为r的圆的参数方程为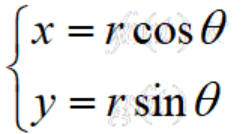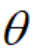，（为参数）；