机器学习十讲(二)
数学知识回顾:
矩阵的逆
-
对于n*n方阵A,如果存在矩阵B使得AB = BA = I,则称B为A的逆矩阵,记为A-1
-
若A为可逆矩阵,则其逆矩阵是唯一的
-
如何判断矩阵是否可逆?
- 行列式不等于0
- 满秩
- 行(或列)向量组线性无关
- ...
import numpy as np
# 格式化numpy输出
np.set_printoptions(formatter={'float': '{:0.2f}'.format})
A = np.array([[4, 5, 1], [0, 8, 3], [9, 4, 7]])
# 求行列式
print("行列式" + str(np.linalg.det(A)))
B = np.linalg.inv(A) # 求逆
print("A的逆矩阵为B:")
print(B)
print("BA:") # 结果验证
print(B.dot(A))
print("AB:")
print(A.dot(B))
回归:
- 回归如今指的用一个或多个自变量来预测因变量的数学方法
- 在机器学习中,回归指的是一类预测变量为连续值的有监督学习方法
在回归模型中,需要预测的变量叫做因变量,用来解释因变量变化的变量叫做自变量
一元线性回归:
- 模型为y = w1x + w0,其中w0,w1为回归系数
- 给定训练集D = {(x1,y1),...(xn,yn)},我们的目标是找到一条直线y = w1x + w0使得所有样本尽可能落在它的附近。
多元线性回归:
-
y = w1x1 + w2x 2+...+ wdxd +w0
-
训练集D = {(x1,y1),...(xn,yn)}
-
...
-
假设训练集的特征部分记为n*(d+1)矩阵X,其中最后一列取值全为1
-
标签部分记为...
-
最小二乘的参数估计,如果变量之间存在较强的共线性,则XTX近似奇异,对参数的估计变得不准确,造成过度拟合现象。
-
解决方法:正则化,主成分回归、偏最小二乘回归
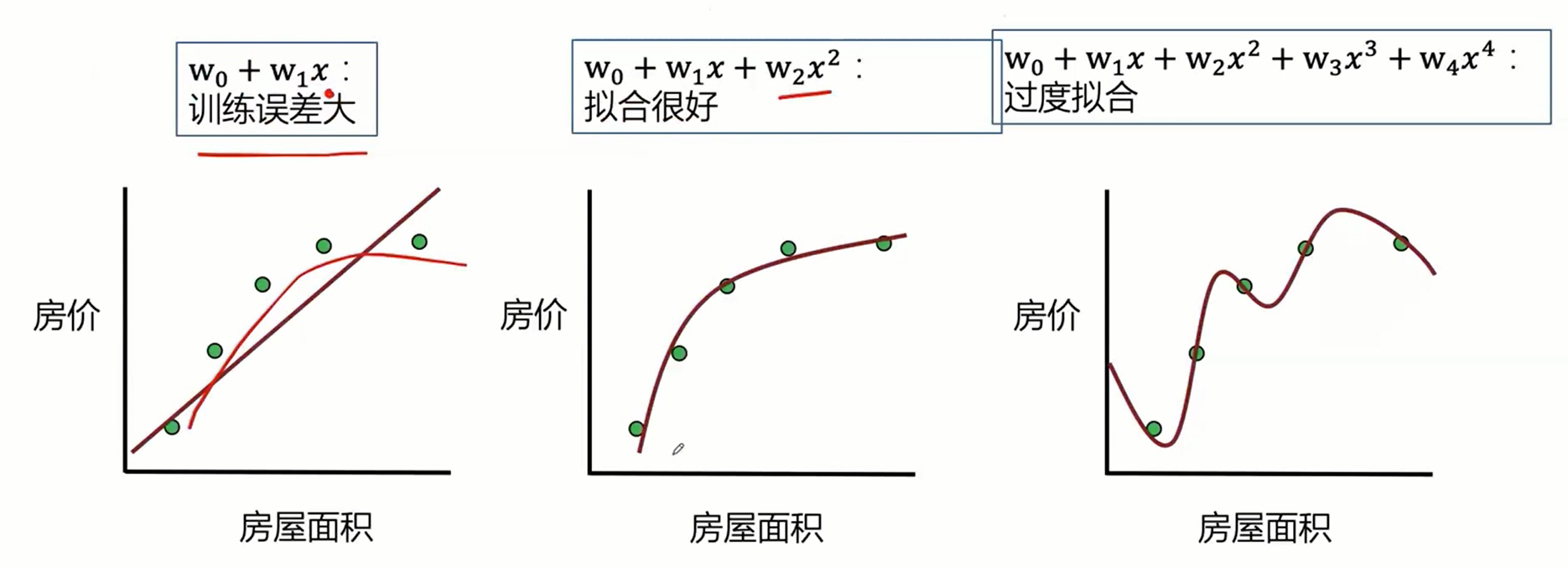
- 正则化可以减小线性回归的过度拟合和多重共线性等问题
岭回归:
- 岭回归:线性回归目标函数加上对W的惩罚函数λ||w||22λ||w||22
- 线性回归目标函数:(Xw−y)T(Xw−y)(Xw−y)T(Xw−y)
- 岭回归目标函数:(Xw−y)T(Xw−y)+λ||w||22(Xw−y)T(Xw−y)+λ||w||22
- 对w求导并令导数等于零易得:xˆridge=(XTX+λI)−1XTyx^ridge=(XTX+λI)−1XTy
- 根据岭迹做超参数λλ的选择(岭迹分析)
LASSO:
- LASSO是一种系数压缩估计法,它的基本思想是通过追求稀疏性自动选择重要的变量
- LASSO的目标函数:(Xw−y)T(Xw−y)+λ||w||1(Xw−y)T(Xw−y)+λ||w||1
- LASSO的解xˆLASSOx^LASSO没有解析表达式,常用的求解算法包括坐标下降法、LARS算法和LSTA算法等
回归模型的评价指标
- 均方误差:MSE(y,yˆ)=1n∑ni=1(yi−yˆi)2MSE(y,y^)=1n∑i=1n(yi−y^i)2
- 均方根误差:RMSE(y,yˆ)=1n∑ni=1(yi−yˆi)2−−−−−−−−−−−−−−√RMSE(y,y^)=1n∑i=1n(yi−y^i)2
- 平均绝对误差:MAE(y,yˆ)=1n∑ni=1|yi−yˆi|MAE(y,y^)=1n∑i=1n|yi−y^i|
- 决定系数:R2(y,yˆ)=1−SSresSStot=1−∑ni=1(yi−yˆi)2∑ni=1(yi−y¯i)2



 浙公网安备 33010602011771号
浙公网安备 33010602011771号