机器学习十讲（三）分门别类，各得其所--分类

1.数学知识回顾：

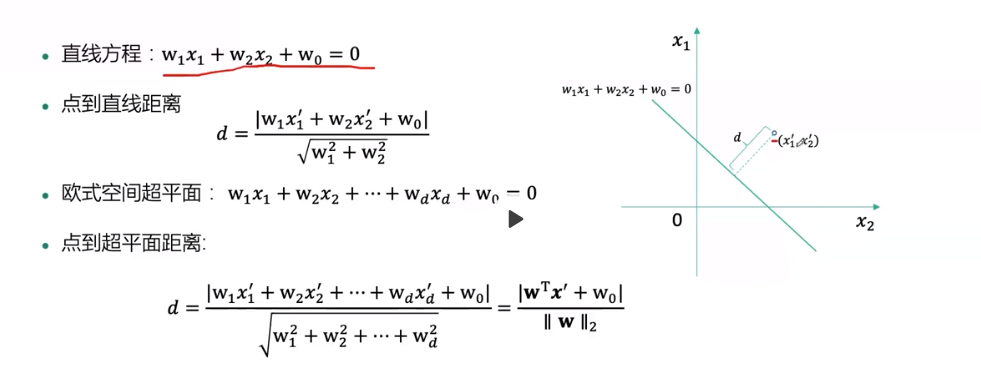
  点到平面的距离：

    

 

 

2.梯度下降法：

 

 

3.随机梯度下降

• 机器学习中，优化目标和梯度具有特定结构：

 

L(W)=∑i=1nl(yi,f(xi;w))∇L(w)=∑i=1n∇l(yi,f(xi;w))=∑i=1n∇Li(w)L(W)=∑i=1nl(yi,f(xi;w))∇L(w)=∑i=1n∇l(yi,f(xi;w))=∑i=1n∇Li(w)

 

• 更新参数只用一个样本的梯度，即随机梯度下降法

 

w(t+1)←w(t)−ηt∇Li(w(t))w(t+1)←w(t)−ηt∇Li(w(t))

 

• 收敛充分条件∑t=1∞ηt=∞∑t=1∞ηt=∞，∑t=1∞η2t<η∑t=1∞ηt2<η
• 需要随着迭代次数的增加降低学习率

4.最大似然估计

• "似然"：likelihood可能性
• 最大似然法，一种求解概率模型参数的方法
• 最早是遗传学家以及统计学家罗纳德·费雪在1912年至1922年间开始使用
• 假设有nn个从概率模型pθ(x)pθ(x)独立生成的样本xini=1xii=1n
• 似然函数L(θ)=∏ni=1pθ(x)L(θ)=∏i=1npθ(x)
• 通过最大化L(θ)L(θ)求解模型参数的方法叫做最大似然法

 

dNLL(θ)L(θ)=∏θm(1−θ)nNLL(θ)=−mlogθ−nlog(1−θ)dNLL(θ)dθ=−mθ+n1−θ,可得θ=mm+n

 

5.如何做分类

• 线性回归：f(x)=wTx,y∈(−∞,+∞)f(x)=wTx,y∈(−∞,+∞)

• 二分类中，y∈−1,1y∈−1,1，用回归的方法做分类，在回归结果上添加映射函数H(f)H(f):

   

  H(f)={+1,f>0−1,f≤0H(f)={+1,f>0−1,f≤0

   

• HH的其他选择：

  • H(f)=tanh(f)H(f)=tanh(f)
  • H(f)=σ(f)=11+e−fH(f)=σ(f)=11+e−f

6.感知机、支持向量机和逻辑回归

• 线性可分训练集D=xi,yini=1,y∈{−1,1}D=xi,yii=1n,y∈{−1,1}
• 感知机：
  • 找到一条直线，将两类数据分开即可
• 支持向量机：
  • 找到一条直线，不仅将两类数据正确分类，还使得数据离直线尽量远
• 逻辑回归：
  • 找到一条直线使得观察到的训练集的“可能性”最大

7.感知机

• f(x)=wTx,w=(w1,w2,...,wd,w0)Tf(x)=wTx,w=(w1,w2,...,wd,w0)T为系数，模型为

 

y=H(f(x))={+1,wTx>0−1,wTx≤0y=H(f(x))={+1,wTx>0−1,wTx≤0

 

• 决策超平面为：wTx=0wTx=0
• 线性可分训练集D=(x1,y1),...,(xn,yn)D=(x1,y1),...,(xn,yn)，点(xi,yi)(xi,yi)到决策超平面的距离为

 

di=|wTxi|||w||2=yiwTxi||w||2→yiwTxi不妨令||w||2=1di=|wTxi|||w||2=yiwTxi||w||2→yiwTxi不妨令||w||2=1

 

• 优化目标：误分类样本离超平面距离之和最小

8.感知机算法

• 输入：训练数据X,yX,y，学习率ηη，迭代步数TT
• 初始化参数W(0)W(0)
• fort=1,...,Tfort=1,...,T
  • 找出误分类样本集合MM；
  • 从MM中随机采样一个样本ii
  • 更新参数w(t+1)←w(t)+ηtyixiw(t+1)←w(t)+ηtyixi
• 输出ww

9.支持向量机

• 线性可分训练集D=(x1,y1),..,(xn,yn),点(xi,yi)D=(x1,y1),..,(xn,yn),点(xi,yi)到决策超平面的距离为di=yiwTxi||w||2di=yiwTxi||w||2

• 间隔：训练集中离超平面最小距离miniyiwTxi||w||2miniyiwTxi||w||2

• 间隔最大化

 

maxwminiyiwTxi||w||2⇔maxw1||w||2miniyiwTximaxwminiyiwTxi||w||2⇔maxw1||w||2miniyiwTxi

 

• 不妨令miniyiwTxi=1miniyiwTxi=1，则上述目标等价于

 

maxw1||w||2⇔minw12||w||22maxw1||w||2⇔minw12||w||22

 

• 非线性：核技巧，映射trick，将数据点从2维空间映射到3维空间，使得数据线性可分

10.逻辑回归

• f(x)=wTx,w=(w1,w2,...,wd,w0)Tf(x)=wTx,w=(w1,w2,...,wd,w0)T为系数
• 训练集D={xi,yi}ni=1,y∈{−1,1}D={xi,yi}i=1n,y∈{−1,1}，概率解释：
  • p(y=1|x)=11+e−wTxp(y=1|x)=11+e−wTx
  • p(y=−1|x)=1−p(y=1|x)=11+e−wTxp(y=−1|x)=1−p(y=1|x)=11+e−wTx
• 考虑到y∈{−1,1}y∈{−1,1}，则样本(xi,yi)(xi,yi)概率为：

 

p(yi|xi)=11+e−yiwTxip(yi|xi)=11+e−yiwTxi