dijkstra算法.

算法的详情就不讲了.

解决的是单源最短路径问题,具体就是一个源点到众多其他结点的距离是否有最短路,且为多少?

 

本质就是按照长度递增次序产生最短路径.

为何长度递增就能产生最短路呢?

原因在于算法本身是基于贪心思想.每一阶段都试图找寻还未确定的点中最有"潜质"的点.    按照的长度递增的战略思路.这是极为重要的.

最后证明一下为何长度递增能导致问题解的正确求解?

下面来解释一下为什么源点到所有可见点的路径中长度最短的一条就一定是源点到该点的最短路径，会不会存在通过一些当前不可见的点间接到达该点的路径比它短呢？

  我们设图G的顶点集合为V，再设一个集合S表示已求得最短路径的终点的集合（S怎么来的下面再说）。

设下一条最短路径（终点为x），那么它只能是弧（v，x）或者通过S中的顶点到达x即（v，vi,....,x）。我们来证明一下：

假设（v，...,x）路径上有一个顶点不在S中，则说明存在一条终点不在S中而长度比此路径还短的路径。但这是不可能的。因为我们按长度递增的顺序来产生各最短路径，所以长度比此路径还短的所有路径均已产生，他们的终点一定在S中。
参考链接:　　https://blog.csdn.net/goodxin_ie/article/details/88707966

下面讲解算法设计的思路.

数据结构:

int n,m[maxn][maxn],vis[maxn],path[maxn],plens[maxn];

分别是,邻接矩阵,是否已经确定,路径,路径长度.

算法过程:

　　初始化以上数据结构.  参见下面代码

　　对所有n个结点进行遍历:

　　　　确定当前层次需要明确的结点.

　　　　更新与当前结点所有关的,且需要更新的结点.

具体就是,双层循环.大循环内要做两个操作.1.确定结点.2.更新未知结点.

以下是相关代码:

仅供参考:

 

#include<iostream>
#include<cstring>
const int maxn=101,MAX=10001;
using namespace std;


int n,m[maxn][maxn],vis[maxn],path[maxn],plens[maxn];
void dijkstra(int start)
{
    plens[start]=0;
    int index;
    for(int i=0;i<n;i++)//确定n-1个点 
    {
        //选出最短的那个作为我们的当前点.
        int MIN=1000000;
        for(int k=0;k<n;k++)
        if(vis[k]==0)
        {
            if(MIN>plens[k])  MIN=plens[k],index=k;
        }
        vis[index]=1;
        //从当前点开始,我们更新其他点的路径和路径长度. 
        for(int j=0;j<n;j++)
        {
            if(vis[j]==0&&m[index][j])
            {
                if(plens[index]+m[index][j]<plens[j])
                {
                    path[j]=index;
                    plens[j]=plens[index]+m[index][j];
                }
            }
        }
    }
}
void init()
{
    for(int i=0;i<n;i++)
    {
        vis[i]=0;
        path[i]=i;
        plens[i]=MAX;
        for(int j=0;j<maxn;j++) m[i][j]=0;//表示不存在. 
    }
    
}
void print()
{
    
    for(int i=1;i<n;i++)
    {
        int j=i;
        while(path[j]!=j)
        {
            cout<<j<<"<----"; j=path[j];
        }
        cout<<0;
        cout<<endl;
    }
    for(int i=0;i<n;i++) cout<<plens[i]<<" ";
}
int main()
{
    int e,x,y,val;
    cin>>n>>e;
    init();
    for(int i=0;i<e;i++)
    {
        cin>>x>>y>>val;
        m[x][y]=val;
    }
    dijkstra(0);
    print();
    return 0;
}


/*
5 8
0 1 5
0 2 2
0 3 6
2 1 1
2 4 5
2 3 3
1 4 1
3 4 2
*/

 

结果是:

 

 

以上结构很清晰.

层次分明.

不过限制性很大.

当然以上代码只是我鉴于动脑又动手的要求而复习巩固的.

只是为了最短路径的学习.

具体的应用就要考虑很多地方.

如:边的存储　　通常可以进行优化,总体来说邻接表要比邻接矩阵要好.

比如代码封装性不好　　可以对结点,结点的边,结点的路径,结点的路径长度都进行相应的封装,例如可以封成类,结构体等.

操作也是如此.

最后就是代码优化了.

可以是编码优化,也可以是时间复杂度优化,不过通常是不存在的.(图的拓扑关系具有一般性) 其次就是数据结构了.

以上有一点很不错的.代码的数据结构还算不错的.如path,plens(路径长度)等.

最后,数据的输入是以下图为例的:

 

 

 

 

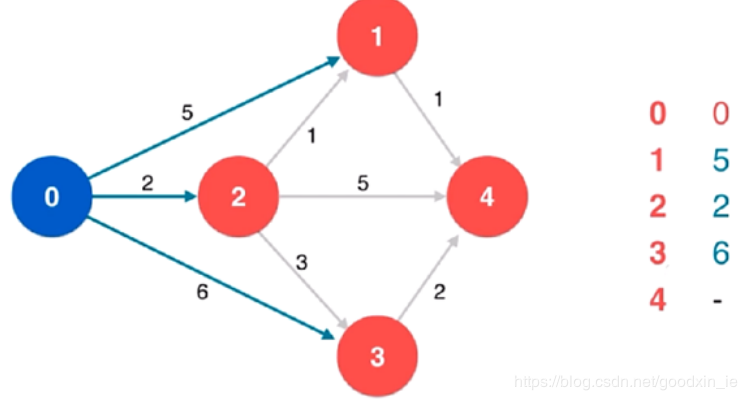
如有错误,欢迎批评指正!